Качество и эффективность метрологического обеспечения, страница 7

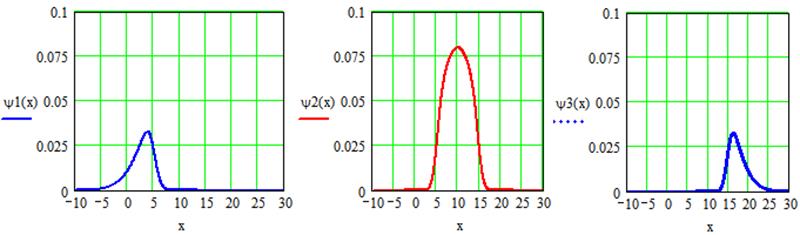
ψ₂(x) - для принятой части ОК;

ψ₃(x)  - для третьей части ОК, у которых показатель качества признан выше области допустимых значений.

Эти распределения определяются следующими выражениями:

,                                                                                (2.3)

,                                                                                (2.4)

.                                                                                 (2.5)

В этих выражениях f(x) и f(y) – плотности вероятностей измеряемого параметра x и аддитивной погрешности измерения y соответственно.

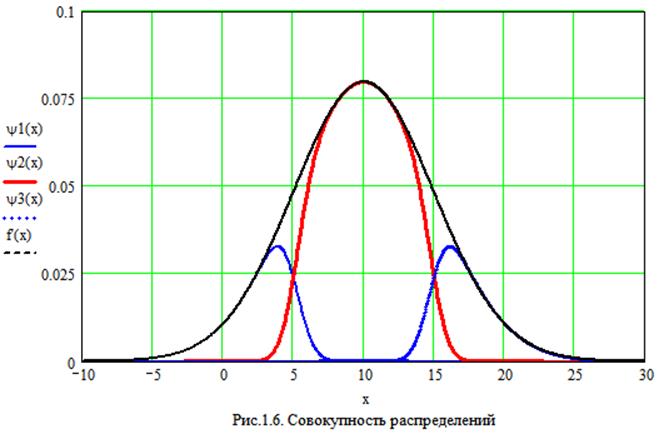
При этом вероятности ошибок первого и второго рода (α и β) определяются по следующим формулам:

,                                      (2.6)

.                                    (2.7)

Пусть распределения параметра х и погрешности измерения у являются гауссовыми:

f(x) = dnorm(x, μ_x, σ_x),

y(x) = dnorm(y, μ_y, σ_y), где μ_x, μ_y – математические ожидания, σ_x, σ_y – среднеквадратические отклонения величин х и у соответственно.

Ошибка первого рода (риск поставщика):

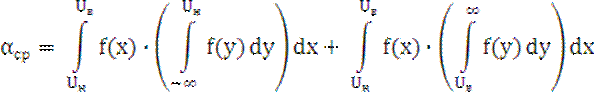
где U_н, U_в – границы поля допуска измеряемого параметра.

Тогда

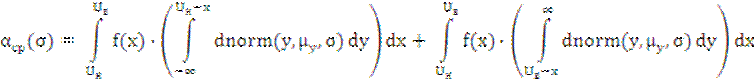
где σ = σ_y – СКО погрешности измерения.

Зависимость α_ср (σ) представлена на рис. 1 при σ = 1, 2…20.

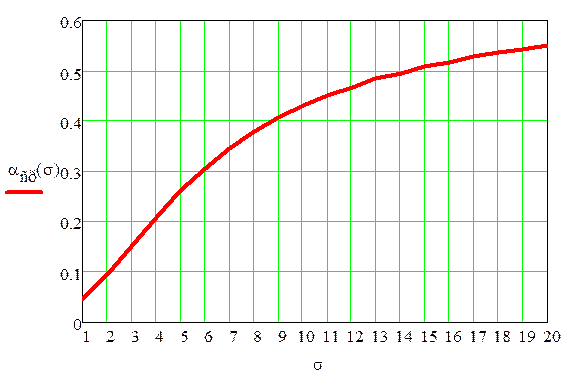
Рис.1. Зависимость ошибки первого рода от СКО погрешности измерения

График построен при следующих значениях:  μ_x = U_ном = 0, μ_у = 0; σ_x = 5; U_в = 5, U_н = -5.

Ошибка второго рода (риск заказчика):

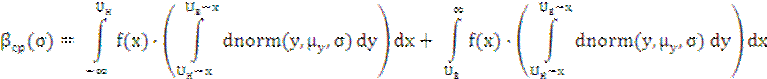
Зависимость β_ср(σ) изображена на рис. 2 при тех же значениях.

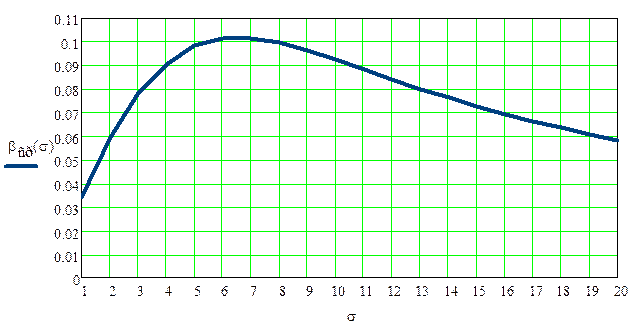
Рис. 2. Зависимость ошибки второго рода от СКО погрешности измерения

Суммарная функция затрат (2.2) при K_U = 1, K_α = 1 и K_β = 10 для σ = 1, 2…10 представлена на рис. 3.

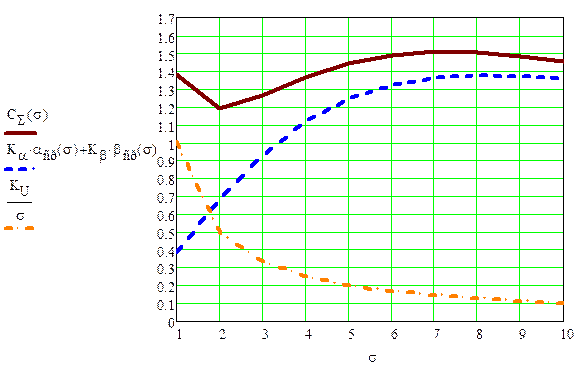
Рис. 3. С_Σ(σ) – суммарная функция затрат; K_α·α_ср(σ) + K_β·β_ср(σ) – затраты на потери из-за ошибок α и β; K_U/σ – затраты на измерение.

По графику на рис.3 можно определить оптимальное значение СКО погрешности измерения, при котором затраты минимальны. Наблюдаемое на рис. 3. уменьшение суммарных затрат определяется уменьшением ошибки второго рода (риска потребителя). Это происходит вследствие того, что при значениях среднеквадратического значения погрешности, больших половины поля допуска, распределение погрешности стремится к равномерному распределению вероятностей, при котором возрастает вероятность брака и ошибка неправильной классификации негодных изделий уменьшается.

Выводы.

1. Параметры изделий (показатели качества), как правило, статистически связаны друг с другом, или, по крайней мере, часть из них. Эти связи устанавливаются на основе статистического анализа выпускаемой продукции с использованием, например, методов корреляционного и регрессионного анализа. Применение этих методов в работах [4,5] для реальных радиотехнических изделий показало их высокую эффективность. Например, при допустимой вероятности риска потребителя, не превышающей значения 0,005, относительное уменьшение числа измерений по сравнению с полным контролем  составляет примерно 60%.

2. Проверка оптимальности выбора точности средств измерений по минимуму затрат на средства измерений, на проведение измерений и затрат, вызванных потерями качества измерений, является одной из основных задач метрологического обеспечения продукции. Используемая модель функции потерь качества измерений, которая позволяет учесть требования на измеряемые параметры, реальные статистические свойства измеряемых параметров и всех составляющих погрешностей измерений.

Исследования функции суммарных затрат, включающих затраты на приобретение средств измерений, на выполнение контрольных операций и затраты, за счёт потерь качества показали наличие минимума затрат. При этом, чем выше стоимость потерь за счёт ошибок измерений, тем резче наблюдаемый минимум. Предлагаемый подход, позволяет устранить необоснованные высокие требования к точности измерений и тем самым уменьшить затраты на приобретение средств измерений и выполнение измерений.

Из рассмотренного примера следует:

1. Для сокращения избыточности контроля многопараметрических изделий РЭА при наличии статистических связей между параметрами предложено использовать метод условных средних.