Качество и эффективность метрологического обеспечения, страница 6

H_ε0(x₁,...,x_n) =.                (2)

Пусть при заданном допустимом уровне вероятности (1) выхода годных изделий Р_{г доп} для распределения W₀ (х₁,..., х_n) выполняется при условии Р_г < Р_{г доп} . Тогда для части параметров       0 < ℓ< n  вводятся  контрольно-регулировочные операции, а для остальной части параметров   (n - ℓ) увеличивается (или оставляется прежней) точность производства продукции ( услуги). При этом формируется новое (апостериорное) распределение вероятностей W_a = (x_1,x₂,...,x_n)при некотором Р_га >Р_{г доп} с соответствующей апостериорной энтропией H_ap   верхняя граница, которой определятся выражением [4]:

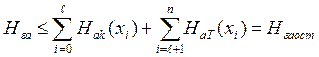(з)

где H_ak(x_i),H_ат(x_i) апостериорные значения энтропии контролируемых и неконтролируемых параметров, соответственно. Знак равенства в (3) выполняется для статически независимых параметров.

Значение сумм в правой части (3) характеризует остаточную неопределенность

значений параметров изделия, возникающих из-за погрешностей контрольно - регулировоч-но операций и конечной технологической точности изготовления. В свою очередь остаточная неопределенность (3) не должна превышать некоторое допустимое значение [2] энтропии

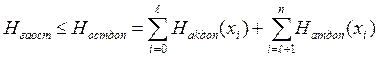,                         (4)

где первая сумма определятся допустимым уровнем ошибок I и II рода (4) (α_доп , β_доп соответственно) при контроле 0 ≤ ℓ ≤ n параметров; вторая сумма - допустимым значениям вероятности брака за счет неконтролируемых (n-ℓ) параметров.

Очевидно, что вероятность брака Р_б = β_нк за счет неконтролируемых параметров является дополнительной составляющей общей ошибки II рода β (риска изготовителя). Тогда необходимо, чтобы выполнялось условие

β = β_k + β_нк ≤ β_доп .                                                               (5)

Остаточная энтропия равна условной энтропии [3], тогда выражение (3) перепишется в виде

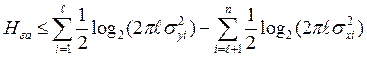           (6)

где ,  - дисперсии параметра x_iи аддитивной ошибки у_iсоответственно (при гауссовых распределениях х, у).

Количество информации, получаемой при контроле 0 < ℓ < n параметров, равно [4] с учетом выражений (2),(3) и (6)

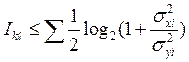.                                      (7)

При функции стоимости С информации, необходимой для измерения параметра х, стоимости потерь  из-за  ошибок I и II рода - С_αi, С_βi, стоимости потерь на брак - C_бi, можно составить общую функцию потерь

.

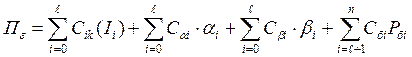Здесь I_i - количество информации при контроле i - го параметра;  ,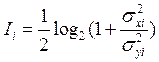

Р_бi, - вероятность брака по i - тому (неконтролируемому параметру).

Таким образом, получена функция потерь (8), позволяющая решить задачу оптимизации выбора контролируемых параметров по критерию минимума затрат (потерь), с учетом погрешности измерения и точности изготовления, а также при обеспечении условий (4) и (5).

Однако необходимо отметить, что для применения функции потерь (8) требуется знание зависимости C_ik (I), которая в общем случае имеет нелинейный характер [1,3].

Полученные выше условия (3) и (4) ограничения числа контролируемых параметров снимают неопределенность условия ограничения числа параметров, предлагаемого в работе [5], что позволяет применять предложенный в данной статье подход на стадии определения номенклатуры параметров изделия.

4 Оценка оптимальности требований к точности измерений.

2.3.1 СЛУЧАЙ АДДИТИВНОЙ ПОГРЕШНОСТИ

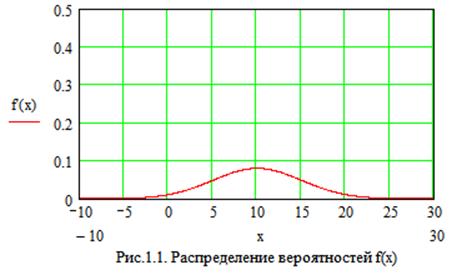
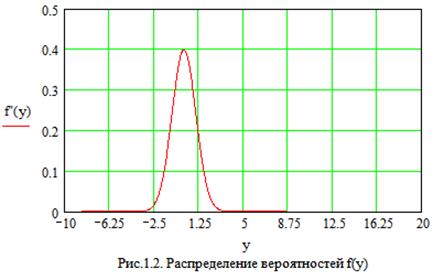
Измеренная величина представляется следующей моделью:

Z(t) = U_с(t) + Y(t),                                           (2.1)

где U_c(t) - истинное значение измеряемого сигнала, Y(t) - аддитивная случайная погрешность, в общем случае зависящие от времени и распределённые по нормальному закону с плотностями вероятности f(x) и f(y) соответственно.

Суммарная функция затрат имеет вид:

,                          (2.2)

где K_U - коэффициент затрат на измерение; K_α и K_β - коэффициенты затрат на потери из-за ошибок α и β; α_ср(σ) -  средняя вероятность ошибки I-ого рода; β_ср(σ) - средняя вероятность ошибки II-ого рода.

Определяем ошибки первого и второго рода с использованием ненормированных функций распределения показателя, которые разделены на три группы [4]:

ψ₁(x) - для первой части объектов контроля (ОК), у которых показатель качества признан ниже области допустимых значений;