Проектирование arc-фильтров, аппроксимация частотных характеристик, страница 29

27

Полюсы s_k передаточной функции фильтра Чебышева являются корнями полинома P_Tn(s) и записываются в виде:

                                                     s_k = σ_pk + jω^/_pk ,                                           (32)

где σ_pk и jω^/_pk – соответственно действительная и мнимая составляющие k-го корня, которые вычисляются по формулам:

 

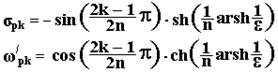                                                                                                           ,              (33)

,              (34)

             где k = 1, 2, …,n.

Полюсы s_k фильтра Чебышева располагаются в левой комплексной s -полуплоскости на эллипсе, уравнение которого имеет вид:

 

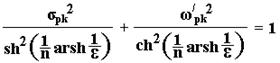                                                                                                             .            (35)

Корни полиномов P_Tn(s) до десятого порядка для неравномерностей затухания в полосе пропускания A_max равных 0,5 dB (ε = 0,349), 1dB (ε = 0,509), 2 dB (ε = 0,765) и 3 dB (ε = 0,998) приведены в таблицах соответственно 8, 9, 10 и 11.

Чтобы представить полином P_Tn(s) знаменателя фильтра Чебышева в виде произведения одного сомножителя первого порядка (если полином нечётного порядка n) и сомножителей второго порядка, необходимо для некомплексно-сопряжённого полюса (если он существует) и для каждой пары комплексно-сопряжённых полюсов, приведённых для соответствующих полиномов в таблицах 8 – 11, составить выражения сомножителей по формулам (20) и (21).