Проектирование arc-фильтров, аппроксимация частотных характеристик, страница 15

Идеальный фильтр характеризуется:

1) нулевыми потерями и нулевыми пульсациями (нулевой неравномерностью) в полосе пропускания;

2) бесконечным задерживанием (затуханием) в полосе задерживания;

3) бесконечной крутизной характеристики затухания на частоте среза ω_С (то есть нулевой шириной переходной области).

Предполагается также, что ФЧХ идеального фильтра является линейной.

16

Так как не существует рациональной передаточной функции, пригодной для точного описания идеального фильтра, то его аналитическое описание аппроксимируют различными функциями. В курсовом проектировании в соответствии с заданием используются два наиболее распространённых вида аппроксимации:

1) полиномами Баттерворта;

2) полиномами Чебышева.

5.2.2. Технические требования к ФНЧ-прототипу

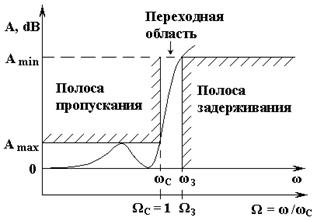Технические требования к фильтрам нижних частот качественно изображены на рисунке 4. Для данного перечня требований к фильтру нижних частот, а именно A_min, A_max, ω_С и ω_З получают соответствующие параметры нормированного ФНЧ-прототипа A_min, A_max, Ω_С =1 и относительную частоту задерживания Ω_З по формуле:

                                              Ω_З = ω_З/ω_С.                                            (12)

В соответствии с полученными нормированными требованиями к ФНЧ-прототипу формируется передаточная функция ФНЧ-прототипа T(s), после чего с помощью преобразования частоты получают передаточную функцию фильтра нижних частот T_ФНЧ(p).

5.2.3. Технические требования к ФНЧ-прототипу