Проектирование arc-фильтров, аппроксимация частотных характеристик, страница 13

Для установившейся частоты p = jω передаточная функция записывается в виде частотной характеристики - комплексного коэффициента передачи:

                               T(jω) = |T(jω)|exp[jφ(ω)],                                       (4) 

где |T(jω)| - модуль комплексного коэффициента передачи или 

                   амплитудно-частотная характеристика (АЧХ) α (ω);

         φ(ω) - аргумент комплексного коэффициента передачи или

                   фазочастотная характеристика (ФЧХ). 

                                                                     

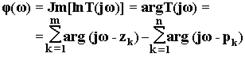
                                                                              .                                (5)

14

Амплитудно-частотная характеристика в децибелах определяется следующим выражением:

                       α_dB(ω) = 20lg |T(jω)| .                                                 (6)

Функция, обратная передаточной функции, называется функцией затухания H(p):

                         H(p) = U_ВХ(p)/ U_ВЫХ(p) = 1/T(p).                                 (7)

Для установившейся частоты p = jω логарифмическая характеристика затухания в децибелах:

                              A(ω) = 20lg |K/T(jω)|,  [dB]                                     (8)

где K - коэффициент усиления.  

5.2. ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНОЙ ФУНКЦИИ

ОБЩЕГО ВИДА ARC-ФИЛЬТРА

5.2.1. Постановка задачи аппроксимации

Передаточную функцию T(p) любого проектируемого фильтра находят на основе прототипа фильтра нижних частот (ФНЧ-прототипа) с передаточной функцией T(s), нормированного (приведённого) относительно частоты среза Ω_С = ω/ω_С =1. Чтобы отличить передаточные функции проектируемых фильтров от передаточных функций их ФНЧ-прототипов, в последних используется комплексная переменная s.