Метод простих ітерацій. Метод Ньютона. Розв’язування систем лінійних алгебраїчних рівнянь (СЛАР)

2.2 Метод простих ітерацій

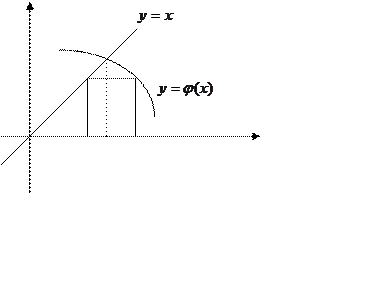
Для використання методу простих ітерацій (послідовних наближень) замінимо рівняння  еквівалентним йому рівнянням

.                                  (2.5)

y

 

  O       a   x₁  x^*    x₀  b                       x

Рисунок 2.2.1

Виберемо деяке наближення  кореня і підставимо його в праву частину рівняння (2.5). Одержимо . Далі обчислюємо за формулою                                (2.6)

Отримуємо послідовність наближень {} до кореня, що у випадку її збіжності до кореня  може дати наближене його значення із заданою точністю . Необхідною і достатньою умовою існування границі послідовності є вимога:  такий, що . З цієї причини шукаємо наближення (ітерації) , які б задовольняли вищезазначеній умові.

Перейти від рівняння  до еквівалентного йому  можна багатьма способами. Але оптимальним є той, що задовольнить достатню умову збіжності методу простої ітерації:  .

При виконанні умови збіжності за початкове наближення  можна взяти довільне значення з інтервалу

2.3 Метод Ньютона

Метод Ньютона (метод дотичних) для наближеного розв’яз-ку рівняння  полягає в побудові ітераційної послідовності ,що збігається до кореня рівняння на відрізку  його локалізації.

                             y

         

                                          

               0           a    x₁           x₀    b                   x

Рисунок 2.3.1

На рисунку 2.3 зображено спосіб отримання першого наближення за методом дотичних: x₁   є точка перетину дотичної, проведеної до кривої в точці з координатами . З прямокутного трикутника, гострий кут якого , маємо

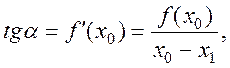 звідки .

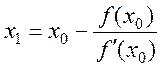Достатні умови збіжності такі. Нехай  - визначена і двічі диференційована на  , причому похідні  зберігають знак на  Тоді , виходячи з початкового наближен-ня  що задовольняє нерівність  ітера-ційна послідовність

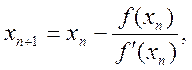
                          (2.7)

збігається до єдиного на  розв’язку рівняння

Для оцінки похибки n-го наближення кореня можна скористатися нерівністю 

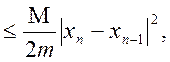                               (2.8)

де  найбільше значення модуля другої похідної  на ; m-найменше значення модуля першої похідної  на .

За необхідності обчислити корінь рівняння з точністю  ітераційну послідовність переривають за умови

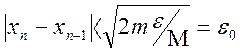                                 (2.9)

 і приймають  за наближене значення кореня

Метод Ньютона ефективний , якщо вибрано вдале початкове наближення для кореня і в околі кореня графік функції має велику кривизну .

Розділ 3

Розв’язування систем лінійних алгебраїчних рівнянь (СЛАР)

Розглянемо систему

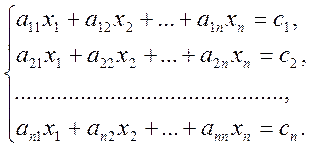                          (3.1)

Її матричний вигляд

Ах=С.                                            (3.2)

Тут  А – {[],(i,j=)}-матриця коефіцієнтів системи,  - вектори-стовпці.

Методи чисельного розв’язку СЛАР поділяються на точні і наближені. Метод вважають точним, якщо, нехтуючи похибками округлення, він дає точний результат після виконання певної кіль-кості обчислювальних операцій. Математичні пакети прикладних програм для ПЕОМ містять стандартні процедури розв’язку СЛАР такими поширеними точними методами, як метод Гаусса , матричним із використанням оберненої матриці .

До наближених методів розв’язку СЛАР відносяться метод простої ітерації та метод Зейделя. Вони дозволяють отримати послідовність  наближень до розв’язку  таку, що .

Ітераційні методи прості, легко програмуються і мають малу похибку округлення, але вони дають збіжну послідовність наближень тільки за виконання певної умови. Це достатня умова збіжності ітераційного процесу: модулі діагональних коефіцієнтів для кожного рівняння системи не повинні бути менше, ніж сума модулів усіх інших коефіцієнтів при невідомих

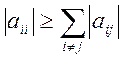.                                      (3.3)

3.1 Метод простої ітерації

Розглянемо СЛАР у матричному вигляді (3.2) (діагональні коефіцієнти a_ii відмінні від нуля для всіх i). Приведемо її до вигляду х=Bх+D, де B=[b_ij] - квадратна матриця порядку n:

         .

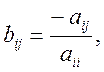
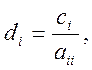
При цьому СЛАР (3.1) набуде вигляду

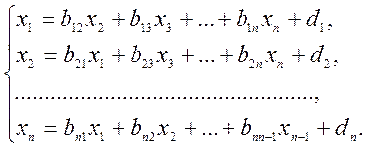                    (3.4)

Взявши довільне початкове наближення , будуємо ітераційний процес за формулою  .

3.2 Метод Зейделя

Ітераційний процес Зейделя відрізняється від методу простої ітерації тим, що при розв’язуванні систем вигляду х=Bх+D обчислення наступного наближення значення x_i при 1<i<n використовується обчислені раніше наближення невідомих x₁,x₂,…,x_i-1…  .

Розглянемо тепер систему Aх=C (3.2) з n рівнянь із n невідомими, як і раніше припускаючи, що діагональні коефіцієнти a_ii відмінні від нуля для всіх i. Перетворимо вихідну систему вигляду Aх=C до вигляду х=Bх+D, де B=[b_ij] - квадратна матриця порядку n:                       .

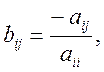
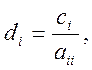
У цьому випадку ітераційний процес  методу Зейделя має вигляд:

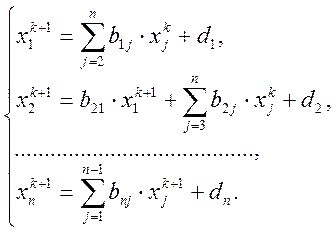                       (3.5)

Часто в практичних обчисленнях ітераційний процес припиняють, якщо два послідовних наближення відрізняються менше від наперед заданого числа ∆ у змісті обраної норми: