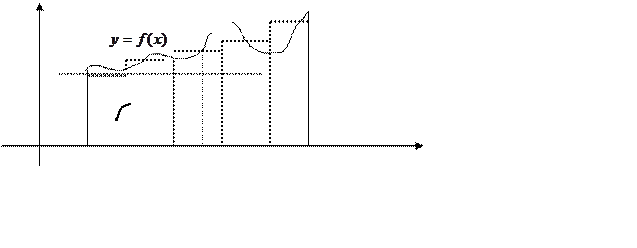
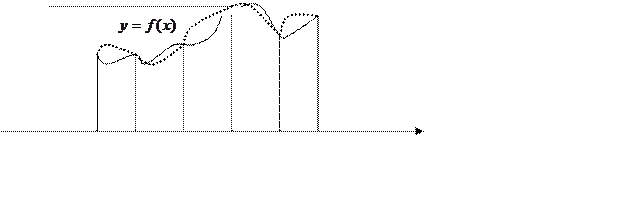
Геометричний зміст визначеного інтегралу полягає в
тому, що він чисельно дорівнює площі криволінійної трапеції, обмеже-ної прямими
y=0, x=a, x=b та функцією ![]() . У самому визна-ченні його
фактично вже закладена основна ідея чисельного інте-грування. Адже шукана площа
може показана як границя інтегральної суми (рисунок 7.1), тобто
. У самому визна-ченні його
фактично вже закладена основна ідея чисельного інте-грування. Адже шукана площа
може показана як границя інтегральної суми (рисунок 7.1), тобто
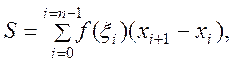 (7.1)
(7.1)
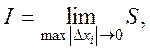 де
де ![]() (7.2)
(7.2)
Обчислення суми ![]() , якщо
не визначати границю, дає найпростіший приклад чисельного інтегрування. А сам
інтеграл можна представити як
, якщо
не визначати границю, дає найпростіший приклад чисельного інтегрування. А сам
інтеграл можна представити як ![]() . Тут
. Тут ![]() називають квадратурною формулою, а
називають квадратурною формулою, а ![]() - похибкою квадратурної формули.
- похибкою квадратурної формули.
Для деяких класів функцій можна записати квадратурні
формули з похибкою ![]() . Такі квадратурні формули
називають точними. Наприклад, для поліномів
. Такі квадратурні формули
називають точними. Наприклад, для поліномів
![]()
квадратурна формула 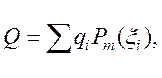
де вибрано довільні точки ![]()
![]() )
і
)
і
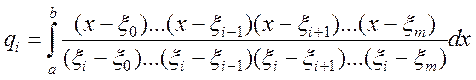
є точною.
Очевидно,
що застосування формули (7.3) для інтегрування поліномів не має сенсу, адже він
легко обчислюється безпосеред-ньо. Практичний зміст точних квадратурних формул
проявляється при інтегруванні таких класів функцій ![]() , які
можуть бути вдало апроксимовані поліномами на інтервалі
, які
можуть бути вдало апроксимовані поліномами на інтервалі ![]() .
Замінивши ними підінтегральну функцію та скориставшись (7.3), можна сподіватись
на малу похибку
.
Замінивши ними підінтегральну функцію та скориставшись (7.3), можна сподіватись
на малу похибку ![]() .
.
7.1 Формула прямокутників
Шукану площу замінимо сумою площ прямокутників, побудованих заміною на
кожному відрізку ![]()
![]() )
функції
)
функції ![]() відрізком прямої
відрізком прямої
![]() ,
, ![]() .
.
 |
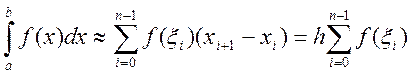 (7.4)
(7.4)
7.2 Формула трапецій
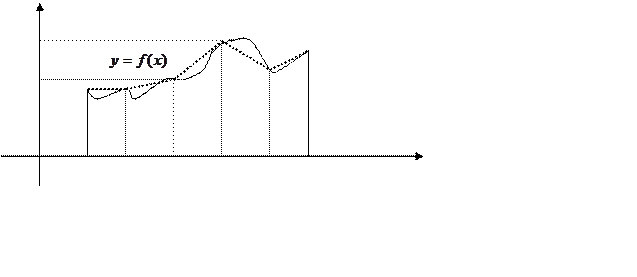 У цьому випадку
підінтегральна функція
У цьому випадку
підінтегральна функція ![]() для
для ![]() заміняється
лінійним сплайном, для якого вузлами інтерполяції будуть точки розбиття
заміняється
лінійним сплайном, для якого вузлами інтерполяції будуть точки розбиття ![]()
![]() ). Загальна площа буде
розгляда-тися як сума площ трапецій, що утворилися ланками ламаної і прямими y=0,
). Загальна площа буде
розгляда-тися як сума площ трапецій, що утворилися ланками ламаної і прямими y=0, ![]() ,
, ![]() на
кожному з інтервалів розбиття.
на
кожному з інтервалів розбиття. ![]() y
y
![]()
![]()
O ![]() x1 … xi
xi+1 …
x1 … xi
xi+1 … ![]() x
x
Враховуючи формулу обчислення площі трапеції, маємо
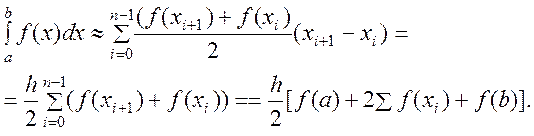
7.3 Формула Сімпсона
![]() Розглянемо один із найбільш відомих і
застосовуваних методів чисельного інтегрування - метод Сімпсона. Розіб'ємо
інтервал інтегрування
Розглянемо один із найбільш відомих і
застосовуваних методів чисельного інтегрування - метод Сімпсона. Розіб'ємо
інтервал інтегрування ![]() [a,b] на парне
число однакових частин із кроком h=(b-a)/(2n). На кожному частковому
відрізку [
[a,b] на парне
число однакових частин із кроком h=(b-a)/(2n). На кожному частковому
відрізку [![]() ] довжини h замінимо функцію f(x)
квадратичним сплай-ном , що інтерполює f(x) у вузлах
] довжини h замінимо функцію f(x)
квадратичним сплай-ном , що інтерполює f(x) у вузлах ![]() .
.![]() y
y
![]()
![]()
![]()
O ![]() x1
… xi xi+1 …
x1
… xi xi+1 … ![]() x
x
Додаючи значення для інтегралів на усіх часткових відріз-ках (i=0,2,...,2(n-1)), одержимо квадратурну формулу Сімпсона (або формулу парабол) :
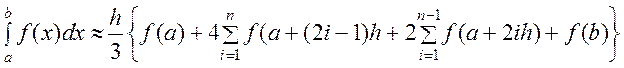 . (7.6)
. (7.6)
Наведемо без доведення похибку апроксимації (обмежен-ня) квадратурної формули Сімпсона в припущенні , що функція f(x) має на відрізку[а,b] неперервні похідні до четвертого порядку :
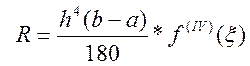 ,
, ![]() .
.
Вона вказує
на те , що для будь-якої неперервної на [a,b] функції f(x)
наближене значення інтеграла , отримане за формулою (7.6) , прагне до точного
значення при ![]() .
.
Зауважимо , однак , що похибка обмеження методу парабол (Сімпсона)
пропорційна ![]() у той час як для методу прямокутни-ків -
у той час як для методу прямокутни-ків - ![]() Це означає , що формула (7.6) відповідає
ряду Тейлора з точністю до членів третього порядку включно ,а формула
прямо-кутників відповідає цьому ряду тільки з точністю до членів першо-го
порядку . Тому при інтегруванні поліному не вище третього степеня метод
Сімпсона дає точні значення інтеграла , адже їхня четверта похідна дорівнює
нулю на [a,b] . Методи прямокутників і трапецій ,як було зазначено
раніше, дають точні значення при інтегруванні поліномів першого ступеня .
Це означає , що формула (7.6) відповідає
ряду Тейлора з точністю до членів третього порядку включно ,а формула
прямо-кутників відповідає цьому ряду тільки з точністю до членів першо-го
порядку . Тому при інтегруванні поліному не вище третього степеня метод
Сімпсона дає точні значення інтеграла , адже їхня четверта похідна дорівнює
нулю на [a,b] . Методи прямокутників і трапецій ,як було зазначено
раніше, дають точні значення при інтегруванні поліномів першого ступеня .
Формула Сімпсона (7.6) є лінійною комбінацією формул прямокутника і трапеції :
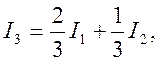
де I1,
I2 і I3-наближені значення інтеграла 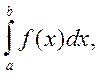 отримані відповідно за формулами
прямокутників, трапецій і Сімпсона .
отримані відповідно за формулами
прямокутників, трапецій і Сімпсона .
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.