Метод простих ітерацій. Метод Ньютона. Розв’язування систем лінійних алгебраїчних рівнянь (СЛАР), страница 3

 Припустімо, що система має лише ізольований розв’язок, що являє собою точку строго мінімуму функції U(x) у n-вимірному просторі .

Нехай x - вектор системи (4.8) і x0 - його нульове наближення. Через точку x0 проведемо поверхню рівня функції U(x). Якщо точка x0 досить близька до кореня x, то при наших припущеннях поверхня рівня

U(x)= U(x0)

буде схожа на еліпсоїд.

З точки x0 рухаємося по нормалі до поверхні U(x)= U(x0) доти, поки ця нормаль не торкнеться в деякій точці x1 якоїсь іншої поверхні рівня U(x)= U(x1).

Потім, відправляючись від точки x1, знову рухаємося по нормалі до поверхні рівня U(x)= U(x1) доти, поки ця нормаль не торкнеться в деякій точці x2 нової поверхні рівня U(x)= U(x2), і т.д.

Оскільки U(x0)>U(x1)>U(x2)>..., то, рухаючись таким шляхом, ми швидко наближаємося до точки з найменшим значенням U ("дно ями"), що відповідає шуканому розв’язку системи (4.8). Позначимо через

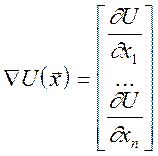
градієнт функції U(x).

Знаходити  потрібний розв’язок за формулою:

Залишається визначити множники . Для цього розглянемо скалярну функцію

Функція F(l) дає зміну рівня функції U уздовж відповідної нормалі до поверхні рівня в точці xp . Множник  треба вибрати таким чином, щоб F(l) мала мінімум. Беручи похідну по l і прирівнюючи її нулеві, одержуємо рівняння

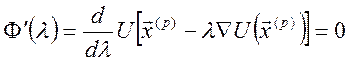.        (4.10)

Найменший додатній корінь цього рівняння і дасть нам значення .

Будемо вважати, що l - мала величина, квадратом і вищими степенями якої можна зневажати. Маємо:

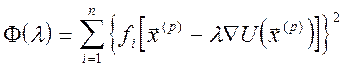
Розкладаючи функції  за степенями l з точністю до лінійних членів, одержимо:

,

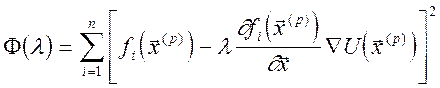де .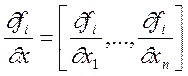

Звідси

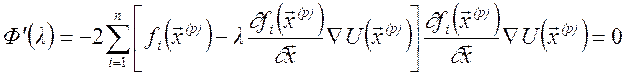
Отже,

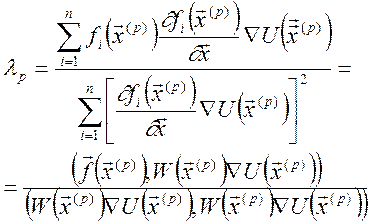, де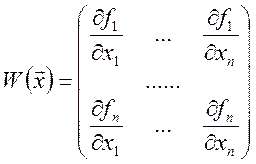

- матриця Якобі векторів-функції f.

Далі, маємо: .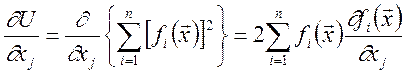

Звідси

,

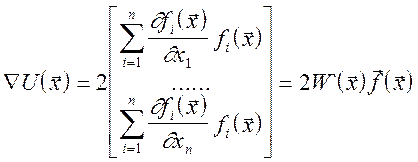де W`(x) - транспонована матриця Якобі.

Тому остаточно

,

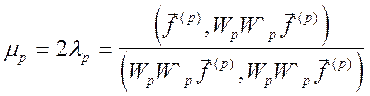причому

.

Чисельна апроксимація функцій

Апроксимація - (від лат. approximo - наближаюся) - заміна одних математичних об'єктів іншими, якомось чином близькими до вихідних. Апроксимація дозволяє досліджувати числові характеристики і якісні властивості об'єкта, зводячи задачу до вивчення більш простих або більш зручних об'єктів (наприклад, таких, характеристики яких легко обчислюються або властивості яких уже відомі). У теорії чисел вивчаються діофантові наближення, зокрема наближення ірраціональних чисел раціональними. У геометрії і топології розглядаються апроксимації кривих, поверхонь, просторів і відображень. Деякі розділи математики цілком присвячені апроксимації, наприклад наближення функцій.

Поняття про наближення функцій

Нехай величина у є функцією аргументу х. Це означає, що будь-якому значенню х з області визначення поставлено у відповідність значення у. Разом з тим на практиці часто невідомий явний зв'язок між у та х, тобто неможливо записати цей зв'язок у вигляді деякої залежності y=f(x). У деяких випадках навіть при відомій залежності y=f(x) вона настільки громіздка (наприклад, містить вирази, що важко обчислюються, складні інтеграли і т.п.), що її використовувати в практичних розрахунках важко.

Найбільш розповсюдженим і практично важливим випадком, коли вигляд зв'язку між параметрами х та у невідомий, є завдання цього зв'язку у вигляді деякої таблиці {x_i, y_i}. Це означає, що дискретній множині значень аргументу {x_i} поставлена у відповідність множина значень функції {y_i} (i=0, 1, …, n). Ці значення - або результати розрахунків, або експериментальні дані. На практиці нам можуть знадобитися значення величини у і в інших точках поза вузлами x_i. Однак одержати ці значення можна лише шляхом дуже складних розрахунків або проведенням дорогих експериментів.

Таким чином, з огляду економії часу і засобів ми приходимо до необхідності використання наявних табличних даних для наближеного обчислення невідомого параметра у при будь-якому значенні (з деякої області) визначального параметра х, оскільки точний зв'язок y = f(x) -  невідомий.

Цій меті підпорядкована задача про наближення (апроксимацію) функцій: дану функцію f(x) потрібно приблизно замінити (апроксимувати) деякою функцією F(x) так, щоб відхилення (у деякому змісті) F(x) від f(x) у заданій області було найменшим. Функція F(x) при цьому називається апроксимуючою.