Метод простих ітерацій. Метод Ньютона. Розв’язування систем лінійних алгебраїчних рівнянь (СЛАР), страница 13

Розглянемо питання про збіжність наближеного розв’язку до точного. Виразимо наближений розв’язок  через точний розв’язок і похибку:. Тоді різницева схема набере вигляду

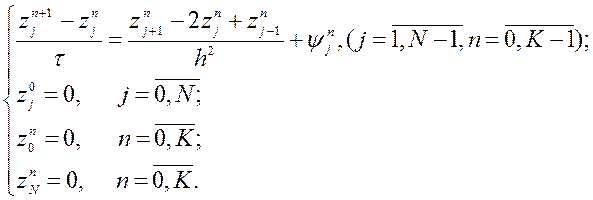
Виразимо з першого рівняння похибку на  часовому шарі

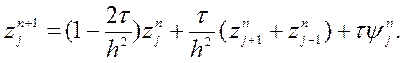
Отримаємо оцінку на похибку

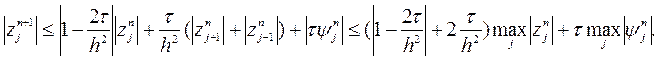
Норму похибки на  часовому шарі визначимо так: 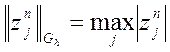. Тоді на  шарі маємо

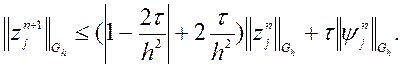
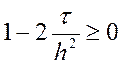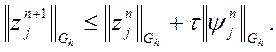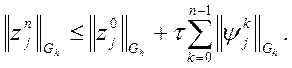Якщо вважати , що накладає обмеження на крок, то Ця оцінка справедлива для будь-якого . Застосувавши її рекурсивно  разів, отримаємо  Але, згідно з умовою, перший доданок справа дорівнює нулю, тому 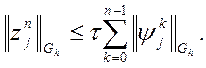Згадаємо про оцінку на нев’язку . Звідси

,

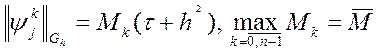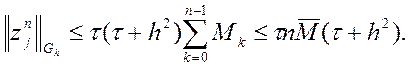
Позначимо  - це константа, яка не залежить від кроку , оскільки . Отримаємо остаточну оцінку

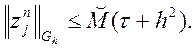
Тобто отримана різницева схема має перший порядок точності по  та другий – по .

                                                                                                                                                                                                                                                         Структура різницевої схеми і задачі для похибки однакова, відмінність лише в тім, що в різницевій схемі права частина дорівнює , а в задачі для похибки - .Отже, за аналогією маємо 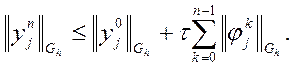Це дискретний аналог принципу максимуму для рівняння теплопровідності. Він свідчить про те, що розв’язок крайової задачі для рівняння теплопровідності є стійким за початковими даними та правою частиною. Але згадаємо, що ця оцінка отримана при обмеженні кроків дискретизації

,

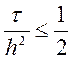тобто побудована різницева схема (9.27) є умовно стійкою. В цьому є істотний недолік таких схем, адже, наприклад, взявши , треба обрати 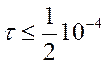. Якщо , то кількість кроків за часом буде 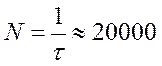. Для того, щоб виправити цей недолік, підійдемо інакше до апроксимації крайової задачі, обравши інший шаблон для побудови різницевої схеми.

9.6.2 Неявна різницева схема

Оберемо шаблон, зображений на рис.9.3 б). Це досягається використанням інших формул чисельної апроксимації відповідних похідних. Рівняння різницевої схеми наберуть вигляду:

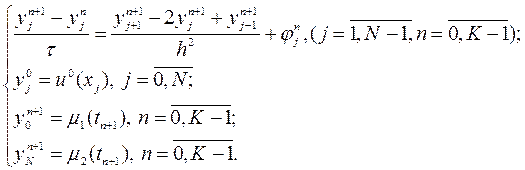 (9.28)

Тоді нев’язка матиме вигляд

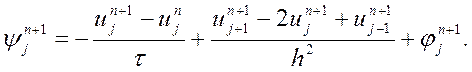    (9.29)

Як і в попередньому випадку, розкладемо та  в ряд Тейлора:

.

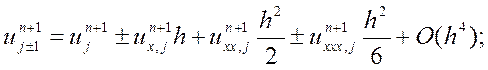
Тепер підставимо ці розкладання в (9.29) і в праву частину додамо та віднімемо  

.

Якщо функцію  взяти такою, що дорівнює  з точністю , то нев’язка набере вигляду

.

Ця різницева схема має перший порядок апроксимації по  і другий по .

Для дослідження на стійкість використаємо метод гармонік. Зіставимо наше різницеве рівняння й: однорідне рівняння

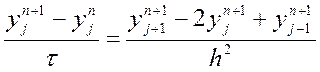.            (9.30)

Дослідимо його на розв’язку вигляду , де  - деякі параметри. Підставимо таке  в (9.30) і скоротимо:

.

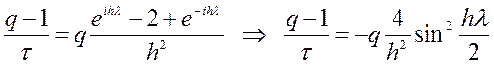Звідси 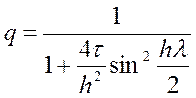. Очевидно, оскільки знаменник завжди не менше ніж 1, що ця неявна різницева схема є абсолютно стійкою, тобто є стійкою при будь-яких значеннях кроків сітки.

Розглянемо проблему розв’язання системи (9.29). Перепишемо перше рівняння з (9.29) так:

.

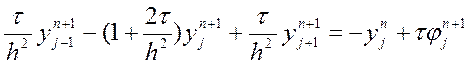Розглянемо його при :

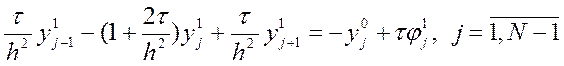
 - це система лінійних алгебраїчних рівнянь відносно , права частина якої повністю визначається початковими умовами, а матриця коефіцієнтів при невідомих має тридіагональну структуру. Отже, можна застосувати метод прогонки. Таким чином, різницева функція може бути визначена у всіх вузлах першого часового шару. Далі застосуємо ті самі міркування для наступних часових шарів, що дозволить знайти значення різницевої функції у всій сітковій області.

9.7 Різницева схема для рівняння гіперболічного типу

Розглянемо крайову задачу для рівняння коливань, що належить до гіперболічного типу:

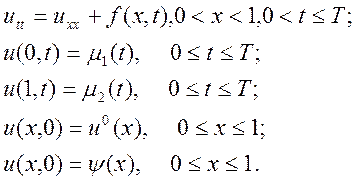                                      (9.32)

Розв’язок такої задачі існує і єдиний.

Уведемо дискретну сітку на розглянутій області.

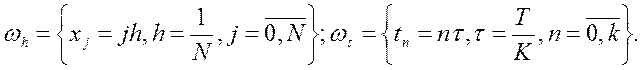
Зауважимо, що початкову умову дають нам значення шуканої функції на границі прямокутника.

Будемо використовувати вже звичні нам позначення: - точний розв’язок у вузлах сітки, - шукане наближення.

Випишемо аналоги крайових і початкових умов

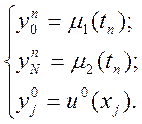
Зіставимо рівняння й дискретний аналог у кожному вузлі сітки. Будемо використовувати шаблон з п'яти точок (рис.9.4г - це мінімально необхідний шаблон для апроксимації других похідних по  і по ).