Метод простих ітерацій. Метод Ньютона. Розв’язування систем лінійних алгебраїчних рівнянь (СЛАР), страница 11

Введемо позначення:

  

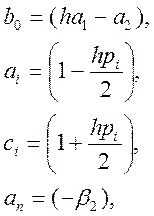
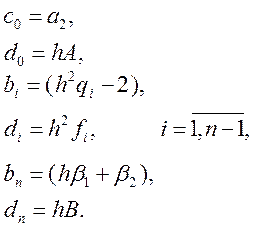
Перепишемо систему з урахуванням введених позначень:

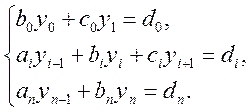
                          (8.15)

Маємо різницеву схему крайового завдання. Запишемо систему рівнянь у розгорнутій матричній формі:

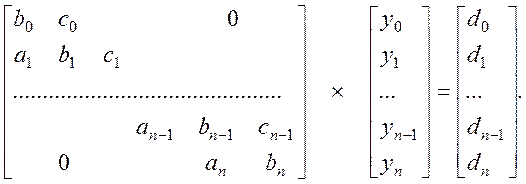
Таким чином, завдання зводиться до розв’язання системи лінійних алгебраїчних рівнянь, що можна записати у вигляді Ay=d.

Виведення формули методу Ейлера, його геометрична інтерпретація,  стійкість, оцінка похибки, вплив обчислювальної похибки.

метод Ейлера для задачі Коші

,                               (8.1)

.                               (8.2)

Для розв’язання задачі потрібно знайти наближені значення  точного розв’язку  рівняння (8.1). Уведемо позначення . Припустимо, що розв’язок  задачі (8.1) — (8.2) у вузлі  відомий. Знайдемо розв’язок у наступному вузлі  . Використовуючи формулу Тейлора, одержимо

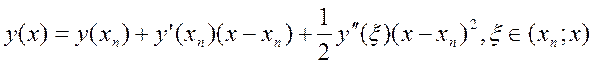 (8.3)

Відзначимо, що похідну , що стоїть у правій частині, можна знайти, диференціюючи рівняння (8.1).

Підставимо у формулі (8.3) , тоді

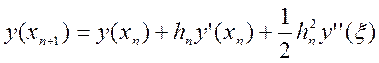.          (8.4)

Припускаючи, що  на відрізку  обмежена, маємо .

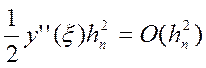Відкидаючи в (8.4) величини другого порядку малості при  в порівнянні з кроком сітки , одержуємо формулу для обчислення наближеного значення  у вузлі  З огляду на те, що , виводимо розрахункову формулу методу Ейлера

.                    (8.5)

Для чисельного розрахунку за формулою (8.5) досить знати . Потім, використовуючи (8.5), можна послідовно знайти значення розв’язку  відповідно в точках

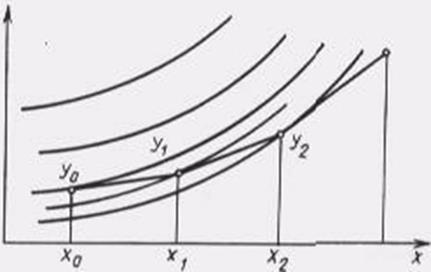
                                                 Рис. – 8.1

Геометрична інтерпретація методу Ейлера показана на рис. 8.1, де зображена множина інтегральних кривих рівняння (8.1).

Припустимо, що початкова умова задана точно. При одержанні (8.5) у формулі Тейлора був відкинутий член, що містить .

На першому кроці, при обчисленні , отримана похибка , яка називається локальною  похибкою, або похибкою на кроці.

На другому кроці  обчислюється за формулою . Величина , знайдена раніше, визначена наближено. Тому сумарна похибка на другому кроці  і так далі.

Метод сіток для наближеного розв’язання крайових задач двовимірних диференціальних рівнянь полягає в такому:

-у плоскій області G, у якій розшукується розв’язок, будується сіткова область G_h (рис. 9.1);

-задане диференціальне рівняння заміняється у вузлах побудованої сітки відповідними різницевими рівняннями;

-на підставі граничних умов визначаються значення шуканого розв’язку в граничних вузлах області Г_h.

Розв’язавши отриману систему різницевих рівнянь, ми знайдемо значення шуканої функції у вузлах сітки, тобто будемо мати числовий розв’язок нашої задачі.

Вибір сіткової області здійснюється залежно від конкретної задачі, але у всіх випадках контур Г_h сіткової області G_h варто обирати так, щоб він якнайкраще апроксимував контур Г заданої області G.

Сітка будується таким чином, щоб вузли (x_i,y_i) сітки G_h або належали області G, або відступали від її границі Г на відстань меншу за h.

Точки (вузли) сітки G_h називаються сусідніми, якщо вони віддалені одна від одної в напрямку вісі Ох або вісі Оу на відстань, що дорівнює кроку сітки h. Вузол A_h сітки G_h називається внутрішнім, якщо він належить області G, а всі чотири сусідні з ним вузли – множині G_h; інакше він називається граничним.

Граничний вузол сітки Г_h називається вузлом першого роду, якщо він має сусіднім внутрішній вузол цієї сітки, інакше – граничний вузол називається вузлом другого роду. Внутрішні вузли і граничні вузли першого роду сітки S_h= називаються розрахунковими точками. Граничні вузли другого роду не входять в обчислення і можуть бути вилучені із сітки.

На перший погляд процедура застосування методу сіток, що складається з трьох етапів, здається простою і такою, що прямо веде до розв’язку. Однак насправді це не так. Через велику розмаїтість типів і розмірів сіток, рівнянь у частинних похідних, граничних і початкових умов, можливих різницевих апроксимацій цих рівнянь і методів їхнього розв’язання, чисельне розв’язання рівнянь у частинних похідних вимагає модифікацій алгоритму при розгляді кожного конкретного випадку.

9.6 Рівняння параболічного типу