Метод простих ітерацій. Метод Ньютона. Розв’язування систем лінійних алгебраїчних рівнянь (СЛАР), страница 14

                                                                                                              Наближення побудуємо так:

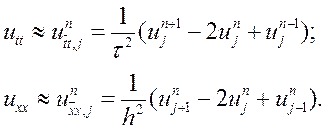
Тоді одержимо таку різницеву схему:

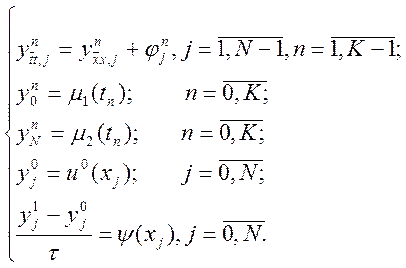       (9.33)

Варто відзначити, що для того щоб різницева схема була збалансованою (тобто щоб не робити зайвих обчислень в одному місці, а потім загрубляти їх в іншому), необхідно, щоб порядки апроксимації в диференціальному рівнянні та у крайовій умові другого типу були узгоджені. Інакше, якщо використовувати низький (перший) порядок апроксимації в крайовій умові, то вся схема буде апроксимувати вихідну задачу з першим порядком апроксимації.

Постараємося всі дані в задачі наблизити з другим порядком точності. Для цього розкладемо  в ряд Тейлора в точці  з залишковим членом другого порядку малості

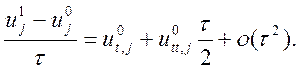
Спробуємо позбутися від . Нехай на границі також виконується рівняння коливання, тоді , і крайова умова набере вигляду

                                                   

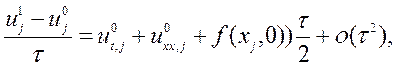
де вираз  точно визначимо із початкових умов.

                                                                                                                            Тоді різницеву схему можна записати у вигляді

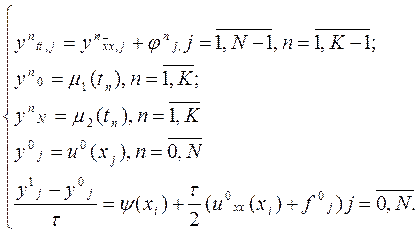
Порядок апроксимації крайової умови буде . Будемо вимагати в задачі другого порядку апроксимації і в першому рівнянні. Для цього достатньо взяти .

Таким чином, різницевий аналог вихідної задачі буде її апроксимувати з другим порядком по  і по h.

Розглянемо питання про визначення наближеного розв’язку. Знайдемо із побудованої різницевої схеми вираз для

.        (9.34)

Покажемо, як визначається  сіткова функція на всій сітці. Розглянемо формулу(9.34) при n=1

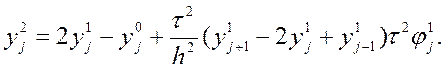
Оскільки  відоме з початкових умов, а  можемо знайти із другої крайової умови, то  знаходиться явно на усьому другому часовому шарі. Аналогічно можна знайти  і так далі, тобто знайти значення шуканої сіткової функції на всій сітці (як і раніше роблячи це пошарово).

                                                                                                                               Як видно із процесу пошуку розв’язку, ця схема – явна і побудований розв’язок буде єдиним.

                                                                                                                Розглянемо питання стійкості. Будемо використовувати відомий нам метод гармонік. Запишемо відповідне однорідне рівняння

.

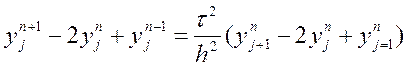                                                                                                                Підставимо в нього розв’язок вигляду , тоді отримаємо

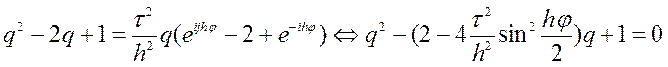
Розв’язки цього квадратного рівняння будуть такими:

.

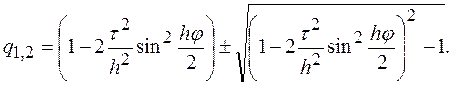Проаналізуємо дискримінант (підкорінний вираз) квадратного рівняння:

1 : оскільки вільний член дорівнює одиниці, то . В цьому випадку (можна показати, що корені не можуть бути протилежними по знаку)  або  більше одиниці, тому стійкості не буде при даних значеннях параметрів.

2 : аналогічно, . Знайдемо значення абсолютної величини кореня

.

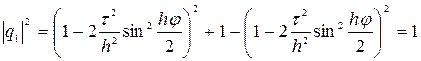Тоді , звідки випливає, що розв’язок буде стійким.

Розпишемо умову недодатності дискримінанту

,

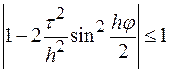або розписавши

.

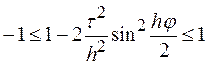Права нерівність виконана завжди, перепишемо ліву

.

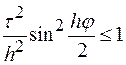У гіршому випадку отримаємо 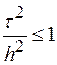, що еквівалентно  (нагадаємо, що в рівнянні теплопровідності ми отримували обмеження вигляду 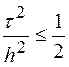). Отримуємо, що побудована схема є умовно стійкою.

Отже, можна виділити кілька особливостей для рівняння коливань:

1)   додаткова умова на апроксимацію;

2)  розв’язок будується пошарово;

3)  умовна стійкість з простими обмеженнями.

9.8 Рівняння еліптичного типу

Прикладом повної математичної постановки задачі для рівняння еліптичного типу є задача з крайовими умовами першого роду, яка має назву задачі Діріхле для рівняння Пуассона

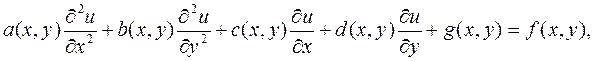 (9.35)

яке задане в однозв'язній області G з границею Г. Коефіцієнти в рівнянні, права частина та границя Г є достатньо гладкими: a(x,y)>0, b(х,у)>О, g(х,у)<0 в G. Потрібно знайти функцію u(х,у), яка задовольняє всередині деякої області G рівняння (9.35), а на границі Г – умову

                         (9.36)