Метод простих ітерацій. Метод Ньютона. Розв’язування систем лінійних алгебраїчних рівнянь (СЛАР), страница 10

При розв’язанні конкретної задачі виникають питання, якою із формул Рунге-Кутта доцільно скористатися і як вибрати крок сітки.

Якщо  неперервна й обмежена разом із своїми четвертими похідними, то гарні результати дає метод четвертого порядку. Він описується системою наступних п'яти співвідношень:

1 

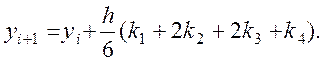
2 

3 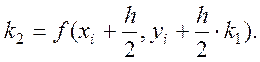                  ();       (8.1)

4 

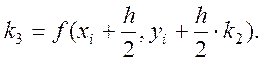
5 

Якщо функція не має зазначених похідних, порядок точності вищенаведеного методу не може бути реалізований. Тоді необхідно користуватися методами меншого порядку точності, що відповідає порядку наявних похідних.

Одним з найбільш простих і досить ефективних методів

 оцінки похибки й уточнення отриманих результатів є правило Рунге. Для оцінки похибки за правилом Рунге порівнюють наближені розв’язки, отримані при різних  кроках сітки. При цьому використовується наступне припущення: глобальна похибка методу порядку p у точці х_i подається у вигляді

 .

За формулою Рунге

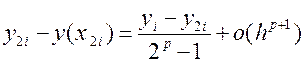 .                          (8.2)

Таким чином, із точністю до (величина більш високого порядку малості) при h→0 похибка методу має вигляд:

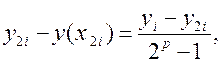                                 (8.3)

де y_i  – наближене значення, отримане в точці з кроком h; y_2i  – із кроком h/2; p  - порядок методу; y(x_2i)  - точний розв’язок задачі.

Формула Рунге для методу четвертого порядку

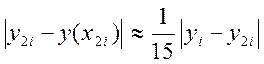 .                       (8.4)

Обчислювальна схема (алгоритм) методу Рунге-Кутта

1  Вибираємо початковий крок h на відрізку [a,b], задаємо точність  .

2  Створюємо множину рівновіддалених точок (вузлів)                          

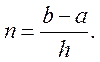
3  Знаходимо розв’язок y_i+1  за формулами при кроку h і при

 кроку h/2, 0 ≤ i ≤ n-1.

4  Перевіряємо нерівність .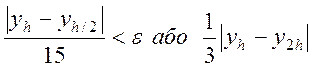

5  Якщо ця нерівність виконується, то приймаємо  і продовжуємо обчислення  з тим же кроком, якщо ні, то зменшуємо початковий крок h у два рази і переходимо до пункту 3.

8.2 Метод прогнозу і корекції

Підправивши схему Эйлера , одержимо схему прогнозу

                            ,                                     (8.5)

де наближене значення . Цю формулу використовувати не можна ,оскільки схема прогнозу нестійка . Тому використовує-мо схему корекції

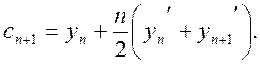                                                                (8.6)

Оцінюючи похибки прогнозу і корекції, одержимо

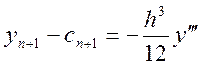  -   похибка корекції,       (8.7)

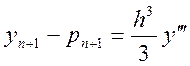               - похибка прогнозу .         (8.8)

Істинне значення лежить між прогнозом і корекцією .На будь-якому кроці можна оцінити точність рішення . При заданому =0,0000001, наприклад, .

Віднімаючи з (8.8) співвідношення (8.7), маємо

                                      .

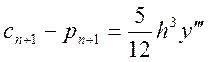Уточнюємо розв’язання, виходячи з формули (8.7):

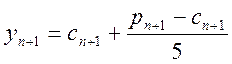                                        .                           (8.9)

Ця формула  завершає схеми прогнозу і корекції .

8.3 Задача Коші для диференціальних рівнянь вищих порядків

Необхідно знайти функцію , що задовольняє диференціальне рівняння та додаткові умови

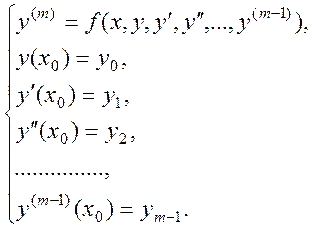                                                                                                       (8.10)

Для розв’язання цієї задачі можна застосувати таку схему зведення до системи диференціальних рівнянь першого порядку:

1  Вводимо нові змінні :

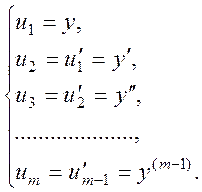
                 (8.11)

                                                                                                                                     2  Розв’язуємо систему з  диференціальних  рівнянь першого порядку.

8.4 Метод кінцевих різниць для розв’язання лінійних крайових задач

Маємо відрізок [a,b]. Потрібно знайти розв’язок лінійного диференціального рівняння другого порядку

  ,                           (8.12)

що задовольняє такі крайові умови:

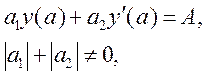
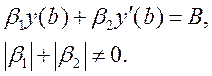                   (8.13)

Виберемо рівномірну сітку: x = a + ih, i = 0,1,2,…,n... Нехай Апроксимуємо  і  у кожному внутрішньому вузлі (i = 1, 2, …, n-1) центральними різницями 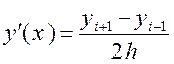,  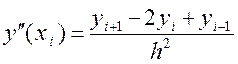і на кінцях відрізка – односторонніми скінченнорізницевими апроксимаціями , .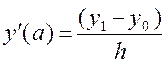

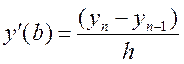Використовуючи ці формули, одержуємо різницеву апроксимацію вихідного крайового завдання:

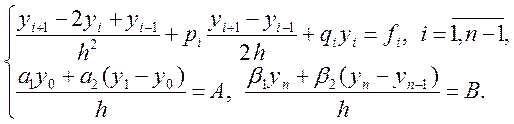        (8.14)

Коефіцієнти різницевих рівнянь залежать від кроку сітки.