Метод простих ітерацій. Метод Ньютона. Розв’язування систем лінійних алгебраїчних рівнянь (СЛАР), страница 9

                                                                                                                           Оцінка похибки квадратурних формул часто виявляється малоефективною через труднощі , пов'язані з оцінкою похідних підінтегральної функції  f(x). У зв'язку з цим набуло поширення практичне правило Рунге оцінки похибки, суть якого полягає в тому , щоб організувавши обчислення двох значень інтеграла за двома множинами вузлів , потім порівняти результати обчислень і одержати оцінку похибки . Найбільш популярне правило пов'язане з обчисленням інтеграла двічі з кроками h і h/2.

Позначимо через I точне значення інтеграла 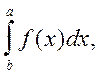 через - його наближене значення , обчислене за однією із квадратурних формул із кроком h, через  наближене значення інтеграла, обчислене за тією ж формулою з кроком h/2. Похибку кожної квадратурної формули з кроком h і h/2 можна записати відповідно у вигляді

    

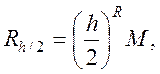
 де R-порядок точності формул, а М-добуток постійної на похідну  Для формул прямокутників і трапецій R=2, для формули Сімпсона R=4.

Обчислимо наближене значення інтеграла за однією і тією ж квадратурною формулою спочатку з кроком h, а потім із кроком h/2. Одержимо

 

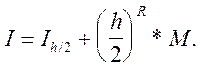
Віднімемо ці рівності :

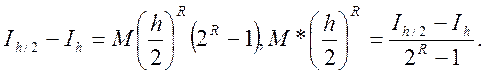
 Одержимо оцінку похибки методом Рунге:

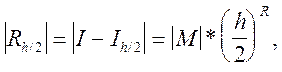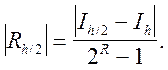 або             (7.7)

Користуючись формулою, можна уточнити наближені значення інтеграла, вважаючи

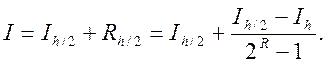                      (7.8)

 Цю формулу називають формулою екстраполяції за Річардсоном.

З огляду на порядок точності квадратурних формул випи-шемо наближену оцінку похибки для формул прямокутників і трапецій за методом Рунге (R=2) :

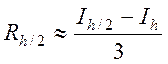                                    (7.9)

 і за формулою Сімпсона (R=4) :

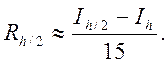                                      (7.10)

 Чисельні методи розв’язання звичайних диференціальних рівнянь

Нехай потрібно чисельно розв’язати задачу Коші для звича-йного диференціального рівняння першого порядку, тобто знайти наближений розв’язок диференціального рівняння  y=F(x,y), що задовольняє початковій умові y(x)=y.Чисельне розв’язання задачі полягає в побудові таблиці наближених значень y,y,y,...,y-розв’язку рівняння y=(x ) у точках x,x,x,...,x - вузлах сітки .

 

                        y                                                        

                       y_n                                                                                   *

                       y₃                                      *

                       y₂                                        *

                       y₁                             *

                       y₀                 *

 

                       O            x₀     x₁    x₂     x₃                   x_n              x

Рисунок 8.1

                                                                                                                      На рисунку * позначені точки, що відповідають наближено-му розв’язку задачі Коші. Треба зазначити, що частіше використо-вують систему рівновіддалених вузлів x =x + ih (i=1,2,..,n) , де h - крок сітки ( h > 0 ) .

8.1 Методи Рунге-Кутта

                                                                                                                               Різні представники цієї категорії методів  потребують більшого чи меншого об’єму обчислень і відповідно забезпечують більшу чи меншу точність. Ці методи мають ряд важливих переваг:

1  Є явними, одноступінчастими, тобто значення  обчислюється за раніше знайденими значеннями .

2  Допускають використання змінного кроку, що дає можливість зменшити його там, де функція швидко змінюється, і збільшити в протилежному випадку.

3  Є легко застосовними, тому що для початку розрахунку досить вибрати сітку  і задати значення .

4  Узгоджуються з рядом Тейлора включно до членів порядку , де ступінь  неоднаковий для різних методів і називається порядком методу.

5  Не потребують обчислення похідних від , а вимагають тільки обчислення самої функції.