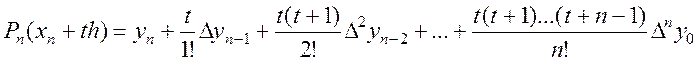Метод простих ітерацій. Метод Ньютона. Розв’язування систем лінійних алгебраїчних рівнянь (СЛАР), страница 6

                                                                                                                                   Як перша, так і друга інтерполяційні формули Ньютона можуть бути використані для екстраполяції функції, тобто для знаходження значень функції , значення аргументів  якої лежать поза таблицею. Якщо  і значення  близьке до , то вигідно використовувати перший інтерполяційний поліном Ньютона, тод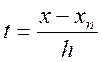і  і  Таким чином, перша інтерполяційна формула Ньютона застосовується для інтерполювання вперед та екстраполювання назад, а друга – навпаки, для інтерполювання назад та екстраполювання вперед.

Зазначимо, що операція екстраполювання, взагалі кажучи, менш точна, ніж операція інтерполювання.

Інтерполяційні формули Ньютона вигідні, оскільки при до-даванні  нових вузлів інтерполяції потрібні додаткові обчислення тільки для  нових членів, без зміни старих.

5.5 Многочлени Чебишева

Як видно з формули (5.14), похибка заміни функції  інтерполяційним многочленом залежить від вибору вузлів інтерполяції . Перш ніж перейти до питання про раціональний вибір вузлів інтерполяції, розглянемо деякі властивості одного з найважливіших й добре вивчених зараз класів спеціальних функцій – многочленів Чебишева першого роду, що часто використовуються для наближення функцій. Многочлен Чебишева  го степеня визначається за формулою

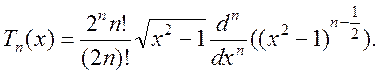                (5.21)

При  з (5.21) отримаємо перші п’ять многочленів першого роду:

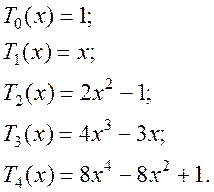
Для визначення многочленів Чебишева часто користуються тригонометричною формою запису

,                     (5.22)

що приводить до таких же виразів для , як і формула (5.21).

Із тотожності

при  маємо рекурентну формулу

.

Многочлен  має  коренів, які можна отримати, розв’язавши рівняння

        або           ;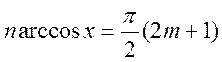

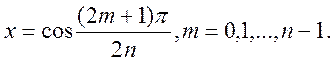              (5.23)

Як видно з (5.22), всі  коренів, що відповідають значенням  знаходяться на відрізку [-1,1], причому ці точки не рівновіддалені, а згущуються ближче до кінця даного відрізка. З формули (5.22) також очевидно, що на відрізку [-1,1]

                                     (5.24)

Доведено, що серед всіх можливих  значень  на відрізку  корені  многочлена  мають ту чудову

 властивість, що для них величина

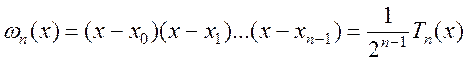             (5.25)

має найменше за абсолютною величиною максимальне значення.

Беручи до уваги (5.24), запишемо

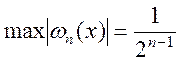.                                   (5.26)

Виходячи з властивостей коренів многочленів Чебишева першого роду і визначення многочлена Лагранжа  -го степеня на відрізку  можна стверджувати, що якщо за  вузлів інтерполювання взяти корені многочлена  то максимальне значення похибки на цьому відрізку буде найменшим для всіх можливих варіантів вибору  вузлів  інтерполювання. Інтерполяційний многочлен, наділений такою властивістю, називається многочленом найкращого наближення. Оцінка (5.14) при цьому набуває вигляду

.

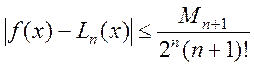Якщо інтерполювання проводиться на довільному відрізку , то заміною змінної

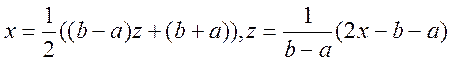
цей відрізок можна звести до відрізка  При цьому корені многочлена  будуть знаходитися в точках

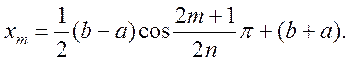
                                                                                                               Оцінка похибки має вигляд

.

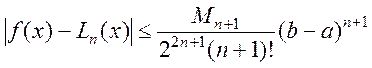5.6 Інтерполяція за допомогою  сплайнів

Підвищення точності інтерполювання вимагає збільшення вузлів інтерполяції. Це призведе до зростання степеня інтерполяційних многочленів. Але в умовах відсутності додаткової інформації про задану таблично функцію останні дають досить значну похибку. В цьому випадку більш ефективним є використання сплайнів, що на проміжку між вузлами інтерполювання є поліномом невисокого степеня. На всьому проміжку інтерполяції  сплайн - це функція, що склеєна з різних частин поліномів. Отже, розглянемо на відрізку  систему вузлів . Сплайном  називається функція, що визначена на , має на ньому неперервні похідні  порядку і на кожному частковому відрізку  збігається з деяким многочленом степеня не вище . При цьому хоча б на одному з відрізків степінь многочлена дорівнює . Якщо , то це  інтерполюючий сплайн.

Лінійний сплайн – це ламана, що проходить через вузли інтерполювання. Рівняння ламаної для