де ![]() (х,у) — задана неперервна функція.
Припускаємо, що f(x,y),
(х,у) — задана неперервна функція.
Припускаємо, що f(x,y),
![]() (х,у) є такі, що розв'язок задачі
(9.35), (9.36) існує, є єдиним і є достатньо гладкою функцією. При f = 0 отримуємо задачу Діріхле для рівняння Лапласа,
однією з важливих властивостей якої є виконання принципу максимуму: неперервний
в G і відмінний від константи розв'язок u(х,у) може досягати свого максимального за модулем значення
тільки на границі Г. Звідси випливає, що є справедливою оцінка
(х,у) є такі, що розв'язок задачі
(9.35), (9.36) існує, є єдиним і є достатньо гладкою функцією. При f = 0 отримуємо задачу Діріхле для рівняння Лапласа,
однією з важливих властивостей якої є виконання принципу максимуму: неперервний
в G і відмінний від константи розв'язок u(х,у) може досягати свого максимального за модулем значення
тільки на границі Г. Звідси випливає, що є справедливою оцінка
![]() , (9.37)
, (9.37)
яка означає стійкість задачі за граничними даними. Вкриємо область G площини (х,у) сіткою
паралельних прямих ![]() , утворивши сітчасту область
вузлів (xi,yk) Gh
з границею Гh (рис.
9.1).
, утворивши сітчасту область
вузлів (xi,yk) Gh
з границею Гh (рис.
9.1).
Замінимо похідні рівняння (9.35) у внутрішніх вузлах різницевими співвідношеннями другого порядку точності апроксимації за формулами:
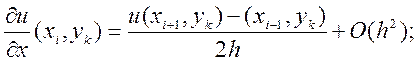
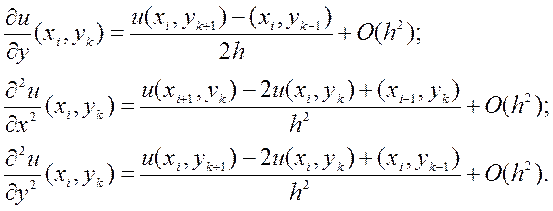
Підставляючи ці співвідношення в (9.35), відкинувши похибку апроксимації
похідних, отримаємо різницеві рівняння для невідомих значень сіткової функції ![]()
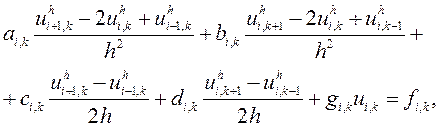 (9.38)
(9.38)
де введені позначення коефіцієнтів і
правої частини у вузлі (хі, yk): аi,k, bi,k,ci,k,
di,k,
gi,k,
fi,k,
(fi,k, = f(хі, уі), (хі,yk) ![]() ). Тут
для внутрішніх вузлів використовувався п’ятиточковий шаблон (дивись рис. 9.3г).
). Тут
для внутрішніх вузлів використовувався п’ятиточковий шаблон (дивись рис. 9.3г).
Співвідношення (9.38) містять, крім невідомих ![]() у
внутрішніх вузлах, ще й невідомі ui,k на границі сітчастої області. Для граничних
вузлів запишемо співвідношення
у
внутрішніх вузлах, ще й невідомі ui,k на границі сітчастої області. Для граничних
вузлів запишемо співвідношення
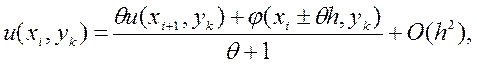 0
0
або 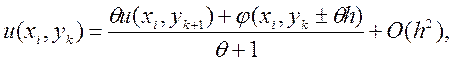
залежно від того, яка точка ![]() , або
, або ![]() ,
, ![]() перетину
неперервної границі Г з лініями сітки знаходиться ближче до граничного
вузла. Ці співвідношення означають, що значення u(хі,ук,)
при (хі,уk)
перетину
неперервної границі Г з лініями сітки знаходиться ближче до граничного
вузла. Ці співвідношення означають, що значення u(хі,ук,)
при (хі,уk)![]() Гh
отримуються лінійною інтерполяцією значень u(x,y) у внутрішньому вузлі
і в точці перетину Г з сіткою. Відкинувши в останніх співвідношеннях
похибку апроксимації, дістанемо вирази для невідомих
Гh
отримуються лінійною інтерполяцією значень u(x,y) у внутрішньому вузлі
і в точці перетину Г з сіткою. Відкинувши в останніх співвідношеннях
похибку апроксимації, дістанемо вирази для невідомих ![]() в
граничних вузлах
в
граничних вузлах
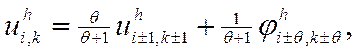 (9.39)
(9.39)
де введено позначення ![]()
![]() Приєднуючи рівняння (9.39) до (9.38),
отримаємо систему лінійних рівнянь відносно
Приєднуючи рівняння (9.39) до (9.38),
отримаємо систему лінійних рівнянь відносно ![]() . У цій
системі число рівнянь дорівнює числу невідомих і числу вузлів в області Gh
. У цій
системі число рівнянь дорівнює числу невідомих і числу вузлів в області Gh![]() Гh.
Гh.
Система рівнянь (9.38), (9.39) — це різницева схема неперервної задачі (9.35), (9.36). Роз’язок цієї різницевої схеми – наближення до точного розв’язку у вузлах (xi,yk).
Для розв’язання системи лінійних рівнянь отриманої різницевої схеми можуть застосовуватися методи, викладені в розділі 2 (метод простої ітерації).
Якщо розв'язок задачі Діріхле для заданої
області і при заданих граничних умовах існує і виражається функцією ![]() і якщо у вузлі з координатами
і якщо у вузлі з координатами ![]() обраної сітки з кроком
обраної сітки з кроком ![]() отримано значення
отримано значення ![]() шуканої
функції, то похибка наближеного розв'язку може бути оцінена нерівністю
шуканої
функції, то похибка наближеного розв'язку може бути оцінена нерівністю![]() де
де ![]() не
залежить від
не
залежить від ![]() .
.
Таким чином, теоретично похибка розв'язку
задачі Діріхле зменшується зі зменшенням кроку сітки як ![]() .
Варто, однак, мати на увазі, що зі зменшенням кроку сітки збільшується число
невідомих і відповідно порядок
.
Варто, однак, мати на увазі, що зі зменшенням кроку сітки збільшується число
невідомих і відповідно порядок ![]() системи лінійних
алгебраїчних рівнянь, а це призводить, як правило, при великих
системи лінійних
алгебраїчних рівнянь, а це призводить, як правило, при великих ![]() до накопичення похибок округлення.
до накопичення похибок округлення.
Припустимо, що ![]() .
Розв’яжемо систему лінійних рівнянь відносно
.
Розв’яжемо систему лінійних рівнянь відносно ![]() методом
простої ітерації згідно з ітераційним процесом:
методом
простої ітерації згідно з ітераційним процесом:
для внутрішніх вузлів
![]()
для граничних вузлів
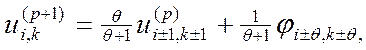 р=0,1,2,…,
р=0,1,2,…, ![]() задане.
задане.
Доведено, що в такому разі послідовні
наближення ![]() збігаються до точного розв’язку різницевої
схеми
збігаються до точного розв’язку різницевої
схеми ![]() або системи рівнянь (9.38),
(9.39) і має місце оцінка
або системи рівнянь (9.38),
(9.39) і має місце оцінка
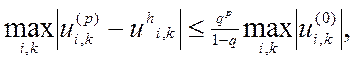
де 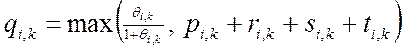 .
.
Доведення цього твердження полягає в
перевірці умови збіжності методу простої ітерації для системи лінійних рівнянь,
при цьому мається на увазі, що невідомий вектор ![]() утворюють
елементи ui,k.. Наприклад, компоненти вектора
утворюють
елементи ui,k.. Наприклад, компоненти вектора ![]() можна перенумерувати таким чином: нехай
можна перенумерувати таким чином: нехай ![]() тоді
тоді
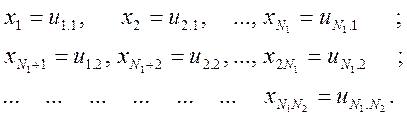
Відносно вектора ![]() =
= ![]() різницева схема є системою лінійних
рівнянь у матричному записі
різницева схема є системою лінійних
рівнянь у матричному записі ![]() де матриця А
має в кожному рядку не більше п’яти елементів
де матриця А
має в кожному рядку не більше п’яти елементів
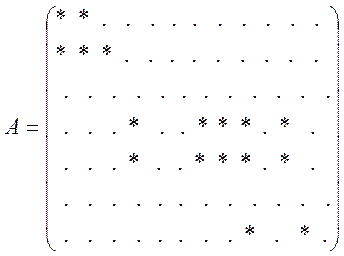
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.