Метод простих ітерацій. Метод Ньютона. Розв’язування систем лінійних алгебраїчних рівнянь (СЛАР), страница 2

тобто коли наближені розв’язки  і   стануть досить близькими і 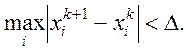 Величина ∆ пов'язана з точністю ε розв’язання системи співвідношенням 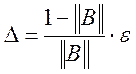, де - норма матриці з коефіцієнтів при невідомих у правих частинах рівнянь перетвореної системи: х=Bх+D. Норма матриці може бути визначена по різному, наприклад, як

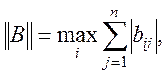 або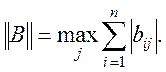

Розв’язання систем нелінійних  рівнянь

                                                                                                       Розглянемо систему нелінійних рівнянь

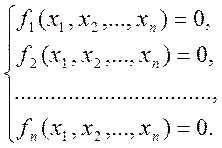                                        (4.1)

                                                                                                                    Для її розв’язання можна застосувати ітераційні методи. Вони дозволяють отримати послідовність наближень . Якщо ітераційний процес збігається, то граничне значення  є розв’язком заданої системи рівнянь. Обов’язковою умовою збіжності є виконання певних вимог до системи, що розглядається.

4.1 Метод простої ітерації

Систему (4.1) наведемо у вигляді

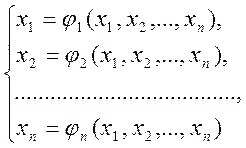                                  (4.2)

 або у векторному вигляді . Причому перехід від системи (4.1) до (4.2) має відбутися тільки за умови, щоб

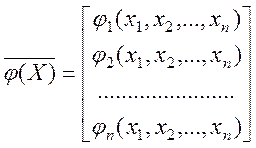
виявилося стискаючим відображенням. Слід зазначити, що загального способу для переходу від (4.1) до (4.2) не існує.

Ітераційна послідовність будується за формулою

,                       (4.3)

де - початкове наближення, яке має бути задано.

Достатньою умовою збіжності ітераційного процесу є виконання умови

,                                     (4.4)

де - матриця з елементами 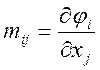 (= 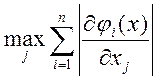- норма матриці ) для довільного  із області визначення розв’язку. Відображення  називають стискаючим, якщо для двох довільних елементів  тасправедливо

,

де коефіцієнт стискання  задовольняє нерівність

4.2 Метод Ньютона для нелінійних систем

При використанні його для нелінійних систем  припускає-ться, що в деякій області  яка містить розв’язок  системи (4.1), функції  мають неперервні похідні першого порядку, і в деякому околі точки  матриця  Якобі   невироджена :

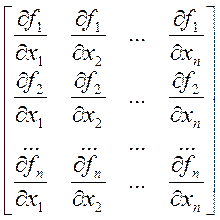 .                        (4.5)

Ітераційний процес будується за формулою

  ,               (4.6)

де , а  - обернена матриця до матриці Якобі. За початкове наближення слід брати вектор розв’язку , достатньо близький до шуканого розв’язку  системи.

Через потребу на кожному кроці розраховувати обернену матрицю обчислювальна формула (4.6) виявляється досить громіздкою. Замість неї зручніше скористатися такою схемою:

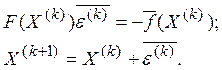                                      (4.7)

При її реалізації для кожного наближення розв’язується система лінійних рівнянь з матрицею , а потім за знайденим приростом  відшукується наступне наближення .

                                                                                                         Недоліком методу Ньютона є те, що при невдалому виборі наближення  ітераційна послідовність не має границі.

Приклад. Методом Ньютона наближено знайти додатний розв’язок системи

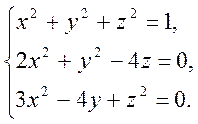
Розв’язок. Позначимо 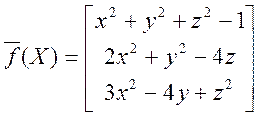. Вибравши за початкове наближення , отримаємо

.

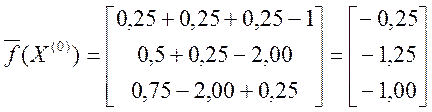                                                                                                        Побудуємо матрицю Якобі

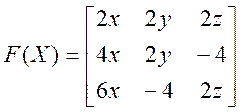, дістанемо  .

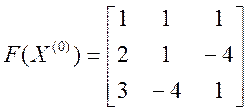Відповідно до (4.7) маємо систему рівнянь

.

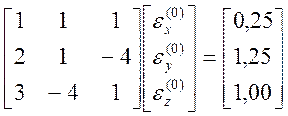Її розв’язок методом Гауса є   

За знайденим приростом дістанемо перше наближення

.

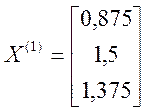Далі обчислюємо друге наближення  Маємо

 .

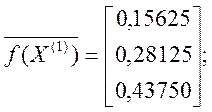
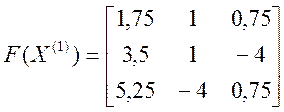Розв’язуючи систему рівнянь , отримуємо

; ;

Використовуючи знайдений приріст, будуємо друге наближення:

.

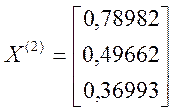Аналогічно знаходимо третє наближення :

    .

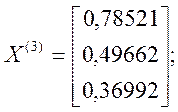
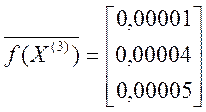Його можна вважати шуканим розв’язком з точністю

4.3 Метод градієнтного спуску

Нехай маємо систему рівнянь

                                     (4.8)

Припустимо, що функції  дійсні і неперервно диференційовані в їхній загальній області визначення. Розглянемо функцію

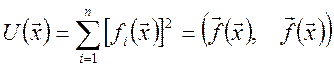         (4.9)

Очевидно,  що кожен розв’язок системи (4.8) перетворює в нуль функцію U(x); навпаки, числа , для яких функція U(x) дорівнює нулеві, є коренем системи (4.8).