Метод простих ітерацій. Метод Ньютона. Розв’язування систем лінійних алгебраїчних рівнянь (СЛАР), страница 16

Це пов’язано з тим, що похідні в кожному внутрішньому вузлі (i,k) апроксимувалися за п’ятьма сусідніми вузлами.

Розв’язання різницевих рівнянь при  збігається до точного розв’язку крайової задачі зі швидкістю, яка визначається порядком апроксимації рівнянь та крайових умов. Таким чином, для точного розв’язку (u(x,y))оцінки похибки

        (9.40)

Оцінка похибки (9.40) є справедливою, якщо точний розв’язок неперервно диференційований чотири рази в області G. Для областей з кутовими точками, наприклад прямокутника, взагалі кажучи, u(x,y) . Але якщо гранична функція, тобто , задовольняє в кутах спеціальні умови узгодження, то точний розв’язок u(x,y) і є правильною оцінка (9.40).

Для прямокутної області G= такими умовами узгодження можуть бути:

достатня гладкість ;

функція повинна задовольняти в кутах прямокутника диференціальне рівняння.

Оцінка похибки (9.40) має в основному теоретичне значення, оскільки містить константу С, яку практично важко визначити,

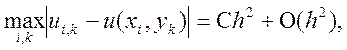
Тому в реальних розрахунках використовується правило Рунге оцінки похибки, аналогічне до того, яке використовується в чисельному розв’язанні задачі Коші і розв’язанні звичайних диференціальних рівнянь. Робиться два варіанти розрахунку  з кроком h та ; тоді похибка має вигляд

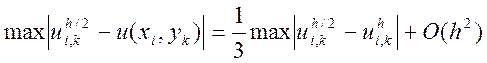
і головна частина похибки визначається на вузлах вихідної сітки.

Необхідно зазначити, що рівномірними прямокутними сітками найбільш зручно користуватися при розв’язанні задач у прямокутних областях. Якщо область має форму паралелограма (скошена система),то користуються координатами, осі яких паралельні сторонам цього паралелограма. Декартові прямокутні координати пов’язані з косокутними координатами  співвідношеннями , де — кут між . У диференціальних виразах похідні по х та у замінюються похідними по . Усі похідні апроксимуються за допомогою центральних різниць. Якщо область має форму кола, зручно користуватися полярними координатами

Наведемо деякі загальні зауваження. При чисельному розв’язанні крайових задач для диференціальних рівнянь у частинних похідних методом сіток можуть бути використані тільки збіжні різницеві схеми, оскільки в цьому разі можна розраховувати на отримання наближеного розв’язку задачі, достатньо близького до точного. Але й збіжні різницеві схеми не завжди можуть бути використані при практичному розв’язанні задачі, оскільки, використовуючи метод сіток, при обчисленні значень граничних функцій та правої частини виникають похибки. Щоб ці похибки не спотворили істинного розв’язку різницевої схеми, остання повинна бути стійкою за граничними умовами і за правою частиною. При використанні нестійкої різницевої схеми спотворення істинного розв’язку тим сильніше, чим дрібніша сітка; при використанні ж великої сітки не можна розраховувати на те, що розв’язок різницевої схеми буде близький до точного розв’язку крайової задачі для диференціального рівняння через погану різницеву апроксимацію рівняння.

Крім того, під час розв’язання різницевої задачі в процесі розрахунків нам обов’язково доведеться округляти значення розв’язків у вузлах сітки. Ці помилки можуть значно спотворити розв’язок, тому необхідною вимогою є стійкість різницевої схеми щодо помилок, які виникають у результаті округлення значень розв’язку в вузлах сітки. Оскільки помилки округлення значень розв’язку в вузлах сітки, принаймні в найпростіших випадках, можна компенсувати зміною правої частини різницевого рівняння, то особливо суттєвою є вимога до стійкості правої частини. Необхідно взяти до уваги й числовий алгоритм, який використовується для розв’язання різницевої схеми. Навіть у випадку, коли різницева схема стійка за граничними умовами і за правою частиною, при невдалому виборі алгоритму для розрахунку розв’язку цієї різницевої схеми може відбутися сильне накопичення обчислювальної похибки, у цьому разі нестійким буде сам процес розрахунку. Нестійкі алгоритми розрахунку практично непридатні у випадку дрібної сітки.