Метод простих ітерацій. Метод Ньютона. Розв’язування систем лінійних алгебраїчних рівнянь (СЛАР), страница 5

На відрізку  задано N точок , що називаються вузлами інтерполяції , і значення деякої функції  в цих точках: . Потрібно побудувати функцію  ( функцію , що інтерполює ) , яка б збігалася з  у вузлах інтерполяції і наближала її між ними, тобто таку,що . Геометрична інтерпретація задачі інтерполяції полягає в тому,щопотрібно знайти таку криву  певного типу, що проходить через задану систему точок  За допомогою цієї кривої можна знайти наближене значення , де  Задача інтерполяції стає однозначною, якщо замість довільної функції  шукати многочлен  степеня не вище , що задовольняє умови

.

Інтерполяційний многочлен  завжди однозначний, оскільки існує тільки один многочлен степеня , що в даних точках набуває заданих значень. Існує декілька способів побудови інтерполяційного многочлена.

Інтерполяційний многочлен Лагранжа, що набуває у вузлах інтерполяції  відповідно значень  має вигляд

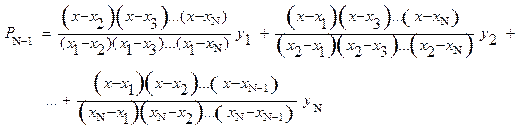          (5.12)

З формули безпосередньо випливає , що степінь многочлена  дорівнює , і многочлен Лагранжа задовольняє всі умови задачі інтерполяції.

Якщо відстань між всіма сусідніми вузлами інтерполювання є однаковою, тобто , формула (6.1) суттєво спрощується. Введемо нову змінну 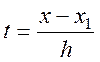, тоді   Інтерполяційний поліном Лагранжа набуде такого вигляду:

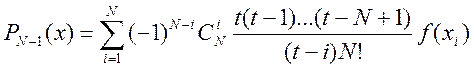.               (5.13)

Тут 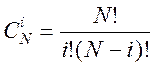. Коефіцієнти, що стоять перед величинами  у формулі (5.13), не залежать ні від функції  ні від кроку , а лише від величин  Тому таблицями, що складені для різних значень , можна скористатися при розв’язуванні різноманітних задач інтерполювання для рівновіддалених вузлів.

Виникає питання, наскільки близько многочлен Лагранжа наближається до функції  в інших точках (не вузлових), тобто наскільки великий залишковий член .На функцію  накладають додаткові обмеження. А саме: припускають, що в розглянутій області  зміни , що містить вузли інтерполяції, функція  має усі похідні  до -го порядку включно. Тоді оцінка для абсолютної похибки інтерполяційної формули Лагранжа має вигляд

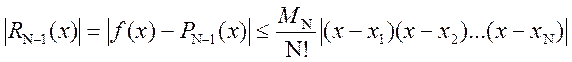,        (5.14)

де  .

5.4 Інтерполяційний поліном Ньютона

Поділеними різницями називають співвідношення вигляду:

- першого порядку:..

 

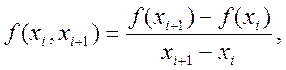
- другого порядку:

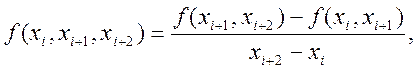
          (5.15)

……………………………………………………………;

- n- го порядку:

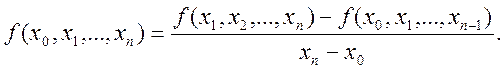
За їх допомогою можна побудувати многочлен

                         (5.16)

Він називається інтерполяційним поліномом Ньютона для заданої функціії . Ця форма запису більш зручна для застосування, оскільки при додаванні до вузлів x₀, x₁, …, x_n нового x_n+1 всі обчислені раніше члени залишаються без зміни, а у формулу додається тільки один доданок. При застосуванні ж формули Лагранжа треба робити всі обчислення знову.

Якщо значення функції задані для рівновіддалених значень аргументу  (постійну величину , i=0,1,…,n називають кроком інтерполяції), то інтерполяційний поліном набуде вигляду

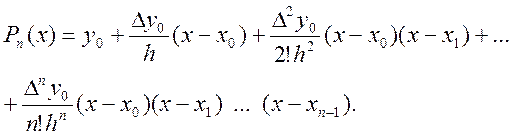                    (5.17)

Тут - скінченні різниці к-го порядку. Вони визначаються за формулою 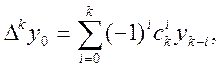  де -біноміальні коефіцієнти.

Порівнюючи цю формулу з попередньою, легко встановити, що при   скінчені і поділені різниці пов'язані співвідношенням вигляду

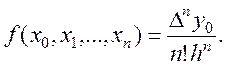                               (5.18)

Для практичного використання формулу (5.17) записують у перетвореному вигляді. Для цього введемо нову змінну , поклавши  де 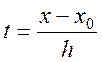 - кількість кроків , необхідних для досягнення точки  із точки . Таким чином отримаємо першу інтерполяційну формулу Ньютона для інтерполювання вперед, тобто на початку таблиці значень:

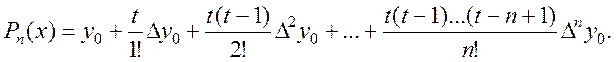  (5.19)

Припустимо, що точка інтерполяції розташована поблизу кінцевої точки  таблиці. У цьому випадку вузли інтерполяції слід брати у порядку  Формула Ньютона для інтерполювання назад тоді матиме вигляд

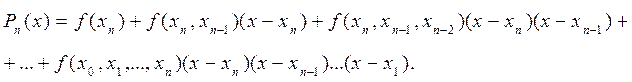(5.20)

Поділені різниці можна виразити через скінчені різниці, якщо скористатися можливістю переставляти в них аргументи, та співвідношенням (5.18), із яких випливає

;    

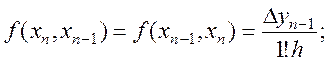
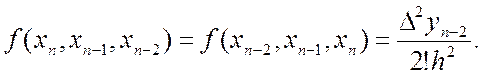
Введемо змінну , поклавши  дістанемо для  другу інтерполяційну формулу Ньютона для інтерполювання в кінці таблиці