Лабораторна робота №5
Варіант № 9
Студент групи ІН-61
ПРОСКОЧИЛО ВЛАДИСЛАВ
1. Умова задачі
Обчислити інтеграл за
формулою Сімпсона з точністю ![]() =0,001.
=0,001.
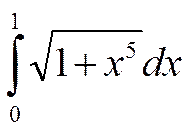 .
.
2. Алгоритм.
Розіб'ємо інтервал інтегрування ![]() [a,b]на парне число однакових частин із кроком h=(b-a)/(2n). На кожному
частковому відрізку [
[a,b]на парне число однакових частин із кроком h=(b-a)/(2n). На кожному
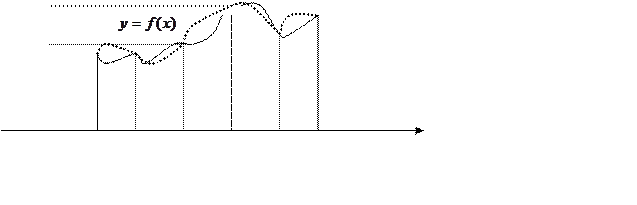
частковому відрізку [![]() ] довжини h замінимо
функцію f(x) квадратичним сплайном , що інтерполює f(x) у вузлах
] довжини h замінимо
функцію f(x) квадратичним сплайном , що інтерполює f(x) у вузлах ![]() .
.
![]() y
y
![]()
![]()
![]()
O
![]() x1 … xi
xi+1 …
x1 … xi
xi+1 … ![]() x
x
Додаючи значення для інтегралів на усіх часткових відріз-ках (i=0,2,...,2(n-1)), одержимо квадратурну формулу Сімпсона (або формулу парабол) :
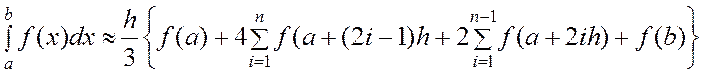 .
.
Апріорна похибка: 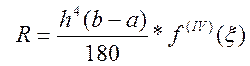 ,
, ![]() .
.
Вона вказує на те ,
що для будь-якої неперервної на [a,b] функції f(x) наближене
значення інтеграла , отримане за формулою Сімпсона, прагне до точного значення
при ![]() .
.
Після обчислення значень інтегралу, можна визначити апостеріорну похибку:
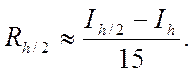
3. Текст программи
Program simpson_metod;
Uses wincrt;
Const eps=0.001;
a=0;
b=1;
Var
n,i: integer;
h,I1,I2,m,R: real;
Function fun(x:real):real;
Begin
fun:=exp(0.5*ln(1+x*sqr(sqr(x))));
End;
Function sum1(n: integer; h: real): real;
var
i: integer;
s1: real;
begin
s1:=0;
for i:=1 to (n div 2) do s1:=s1+fun(a+(2*i-1)*h);
sum1:=s1;
end;
Function sum2(n: integer; h: real): real;
var
i: integer;
s2: real;
begin
s2:=0;
for i:=2 to (n div 2) do s2:=s2+fun(a+(2*i-2)*h);
sum2:=s2;
end;
begin
n:=2;
h:=(b-a)/n;
repeat
I1:=(h*(fun(a)+fun(b)+4*sum1(n,h)+2*sum2(n,h)))/3;
n:=2*n;
h:=(b-a)/n;
I2:=(h*(fun(a)+fun(b)+4*sum1(n,h)+2*sum2(n,h)))/3;
m:=abs(I1-I2);
until (m<eps);
r:=m/15;
writeln;
writeln('Result:');
writeln;
Writeln('Integral = ',I2:1:4);
writeln('R = ',r:1:10);
end.
Результати програми:

перевірка в Maple:
> F:=(1+x^5)^(1/2);
![]()
> F1 := int((1+x^5)^(1/2),x=0..1.);
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.