Розв’язання задачі Дірихле для рівняння Лапласа методом сіток (Лабораторна робота № 9)

Міністерство освіти і науки України

Сумський державний університет

Кафедра інформатики

Лабораторна робота №9

з дисципліни

«Чисельні методи»

на тему:

«Розв’язання задачі Дірихле для рівняння Лапласа методом сіток»

Варіант 3

Підготувала

студентка ПМ-71

Білоус Т.В.

Перевірила

Назаренко Л.Д.

Суми 2009

Постановка задачі

В настоящей лабораторной работе методом сеток требуется решить задачу Дирихле для частного случая уравнения Пуассона-Лапласа  в прямоугольной области.

       Задача ставится следующим образом: найти функцию , удовлетворяющую внутри прямоугольной области уравнению Лапласа и принимающую на границе области заданные значения, т.е.

      

      

где заданные функции.

Математичне обґрунтування та вибір алгоритму розв’язання задачі

Будем считать, что непрерывна на границе области , т.е.

f1(0)=f3(0), f1(b)=f4(0), f4(b)=f2(a), f3(a)=f2(0).

Проверим это:

f1(0)= - 0*0 + 1 = 1;

f3(0)= sin(0) – (1 + sin(1))*0*0*0 + 1 = 1.

f1(b)= - b*b+1 = f4(0)=0;   b*b=1;   b=1;

f4(b)= b = 1 = f2(a) = a;   a=b,   a=1;

Для окончательной проверки подставим в последнее уравнение имеющееся значение a:

f2(0)= 0 = f3(a) = sin(1) – (1 + sin(1))*1*1*1 + 1 = 0.

Сошлось.

Выбрав шаг = 0.2, строим сетку где

Для уравнения Лапласа итерационная формула (14) запишется следующим образом:

         

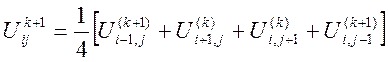
При последовательность  сходится к точному решению . В качестве условия окончания итерационного процесса можно принять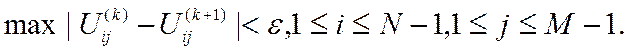

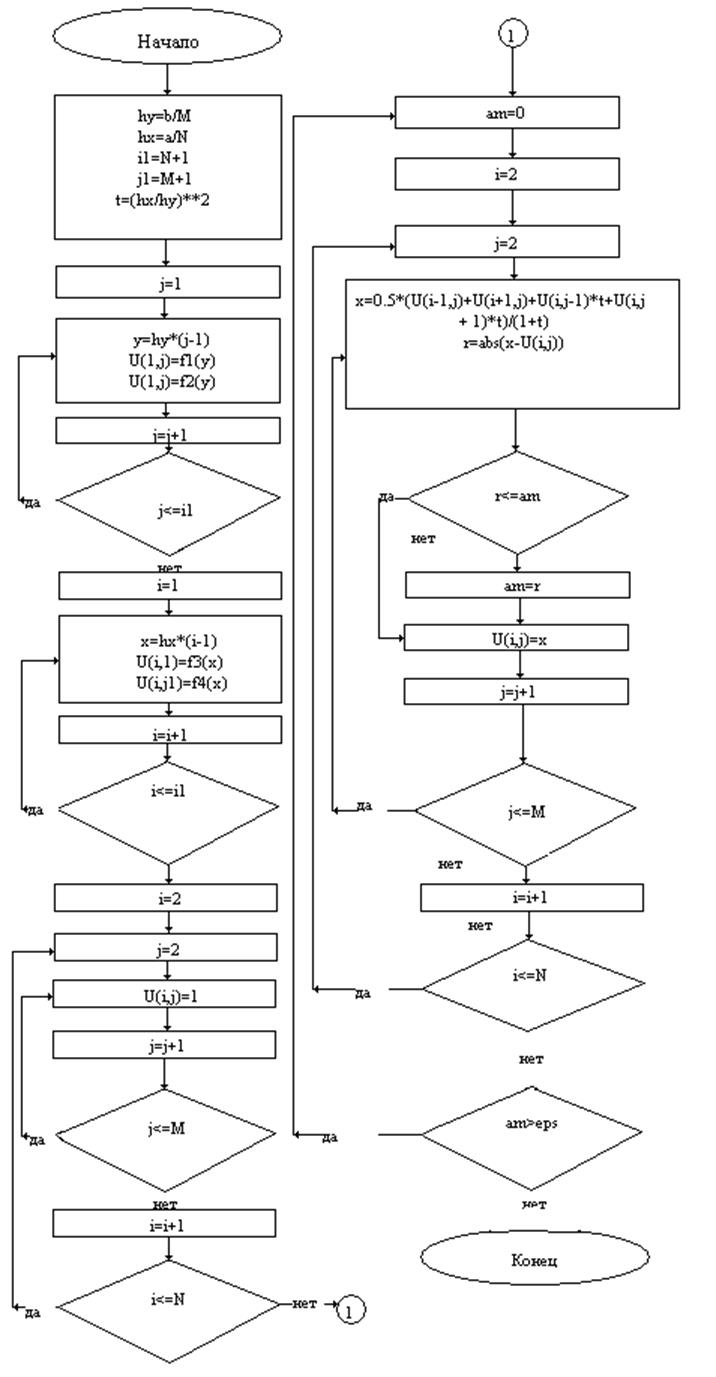
На рисунке представлена блок-схема описанного выше алгоритма решения задачи Дирихле. Входные параметры: значение , правый конец отрезкаколичество шагов сетки по ; значение , правый конец отрезка - количество шагов по ; значение  из условия окончания итерационного процесса.

          Выходной параметр:  - двух мерный массив из действительных чисел, содержащий значение решения в узлах сетки.

Програмна реалізація алгоритму

Текст програми:

#include<stdio.h>

#include<conio.h>

#include<math.h>

#include<stdlib.h>

#define a 1

#define b 1

#define m 5

#define n 5

#define eps 0.0001

float f1 (float y)

{

 return -y*y+1;

}

float f2 (float y)

{

 return y;

}

float f3 (float x)

{

 return sin(x)-(1+sin(1))*pow(x,3)+1;

}

float f4 (float x)

{

 return x;

}

void main()

{

 float hy,hx,t,u[n+1][m+1],x,y,am,v,r;

 int i,j;

 clrscr();

 hy=(float)b/m;

 hx=(float)a/n;

 t=(hx/hy)*(hx/hy);

 for(j=0;j<=m;j++)

 {

  y=hy*j;

  u[0][j]=f1(y);

  u[n][j]=f2(y);

 }

 for(i=0;i<=n;i++)

 {

  x=hx*i;

  u[i][0]=f3(x);

  u[i][m]=f4(x);

 }

 for(i=1;i<n;i++)

  for(j=1;j<m;j++)

   u[i][j]=1;

 do

  {

   am=0;

   for(i=1;i<n;i++)

    for(j=1;j<m;j++)

     {

      v=(0.5)*(u[i-1][j]+u[i+1][j]+u[i][j-1]*t+u[i][j+1]*t)/(t+1);

      r=fabs(v-u[i][j]);

      if(r<=am)

      u[i][j]=v;

      else

      {

      am=r;

      u[i][j]=v;

      }

   }

  }

 while(am>eps);

 for(i=0;i<=n;i++)

  {for(j=0;j<=m;j++)

   printf("%2.2f  ",u[i][j]);

   printf("\n");}

getch();

}

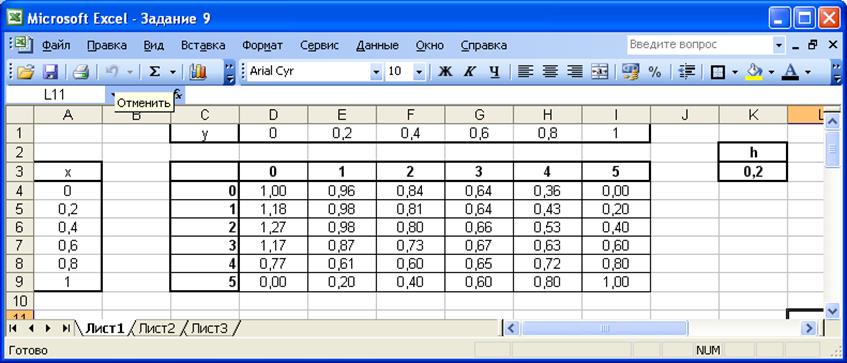
Результат виконання програми:

Пакетна реалізація алгоритму

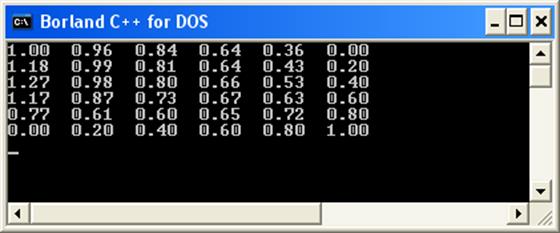
Введемо до таблиці значення крайніх точок заданої області – тих, що розраховуються за допомогою функцій, взятих з умові. Інші точки знайдемо, користуючись формулою 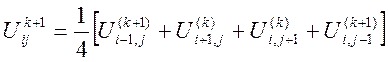. Отримаємо і розв’яжемо систему з шістнадцяти рівнянь з шістнадцятьма невідомими. Доповнимо отриманими значеннями таблицю.

Висновки

У даній лабораторній роботі було чисельно розв’язано задачу Дірихле для рівняння Лапласа методом сіток.

Дане завдання було виконане програмно і пакетно. Результати, отримані за допомогою Сі та Excel, збігаються.