Лабораторна робота №1
Розв’язати нелінійне
рівняння sin(x+![]() -0,5x=0 з точністю
-0,5x=0 з точністю ![]() :
:
Знайдемо розв’язок рівняння за допомогою методу Ньютона
Рівняння
sin(x+![]() -0,5x=0
-0,5x=0
має корінь на відрізку [1..2], тому що f(1)=0,38865>0, a f(2)=-0,90575<0.
Так як ![]() - визначена і двічі
диференційована на [1..2] , причому похідні
- визначена і двічі
диференційована на [1..2] , причому похідні ![]() зберігають
знак на [1..2] (
зберігають
знак на [1..2] (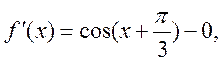
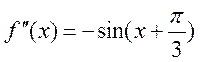 , збереження знаків похідних видно на графіку 1
і 2 відповідно)
, збереження знаків похідних видно на графіку 1
і 2 відповідно)
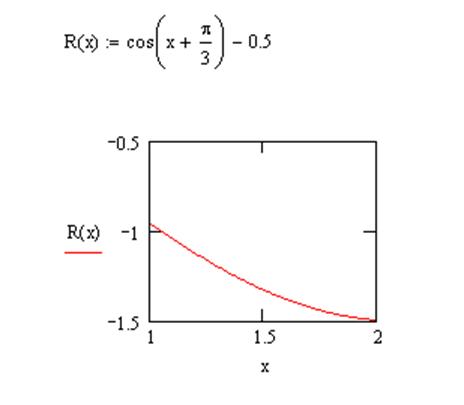
графік 1 (перша похідна)
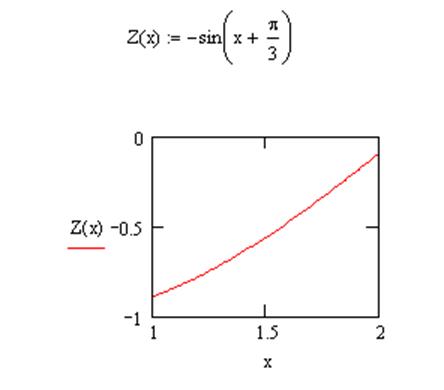
графік 2 (друга похідна)
Тоді , виходячи з
початкового наближення ![]() що
задовольняє нерівність
що
задовольняє нерівність ![]() ітераційна
послідовність
ітераційна
послідовність
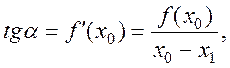 звідки
звідки 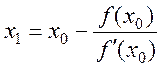 ,
, 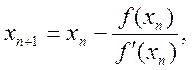
![]()
Вибираємо
початкове наближення кореня ![]() так, щоб
так, щоб ![]() Вибираємо
Вибираємо ![]() , тому
що
, тому
що ![]() (
(![]()
![]() )
)
Ітерації будемо віконувати в середовищі програмування Borland Pascal:
Program chm1;
uses WinCRT;
var x, xx : real;
n : integer;
const e=0.0001;
begin
n := 0; xx:=2;
while (abs(xx-x)>e) do
begin
x := xx;
xx := x-((sin(x+pi/3)-0.5*x)/(cos(x+pi/3)-0.5));
n := n+1;
writeln ('pri n=',n,' ',((xx+x)/2):9:8);
end;
readln;
end.
Корінь х=1.35204424 отриманий на 4-й ітерації:
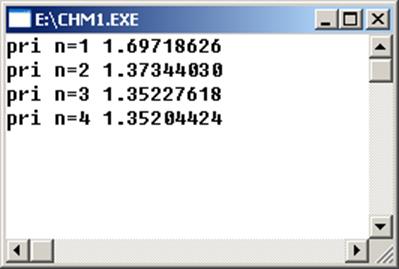
Перевіримо результати обчислень, побудувавши графік в Mathcad:
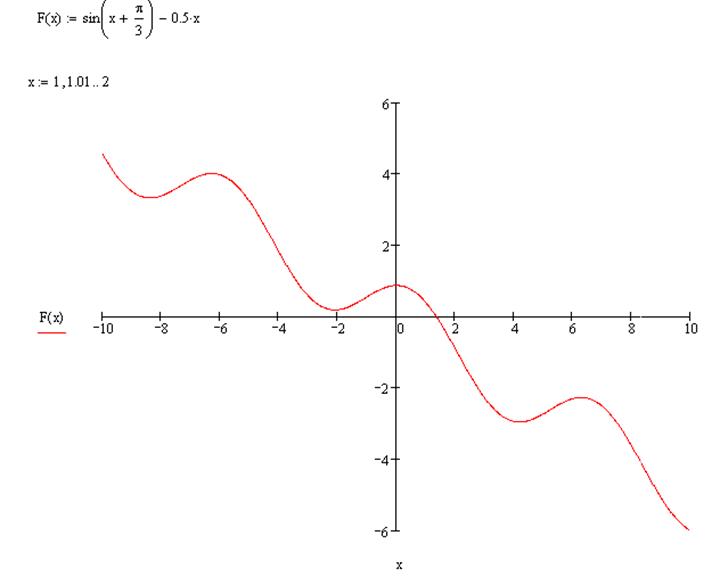
Розв’язок даного рівняння в Mathcad:
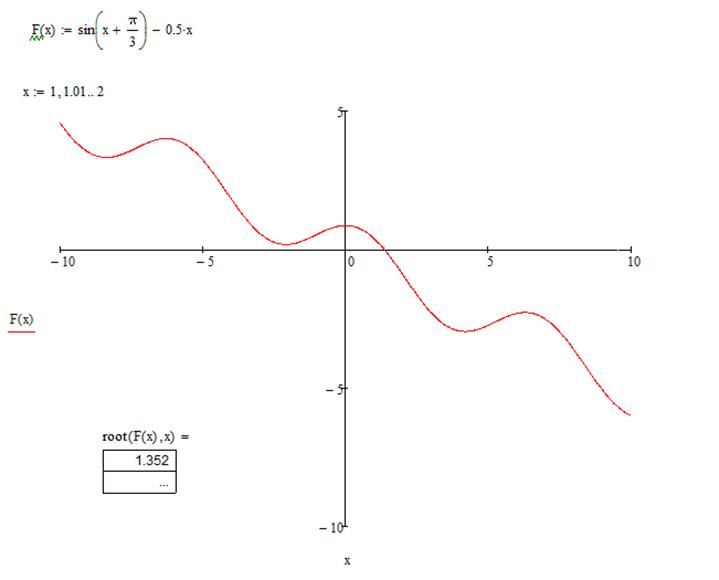
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.