Лабораторна робота №2
Завдання 2 Методом Зейделя розв’язати систему лінійних алгебраїчних рівнянь вигляду АХ=В із точністю до 0,0001.
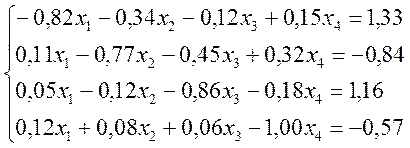
Перевіримо достатню умову збіжності ітераційного процесу для метода Зейделя. Вона полягає в тому, що абсолютна величина коефіцієнта, який стоїть на головній діагоналі матриці А повинна бути більшою за суму абсолютних величин інших чисел цього рядка матриці А.
Перевіримо цю умову.
Для першого рядка маємо
½ -0,82 ½ > ½-0,34½ + ½-0,12½ +½0,15½ = 0,61 умова виконується.
Для другого рядка маємо
½ -0,77 ½ < ½0,11½ + ½-0,45½ +½0,32½ = 0,88 умова не виконується.
Для третього рядка маємо
½ -0,86 ½ > ½0,05½ + ½-0,12½ +½-0,18½ = 0,35 умова виконується.
Для четвертого рядка маємо
½ -1,00 ½ > ½0,12½ + ½0,08½ +½0,18½ = 0,38 умова виконується.
Тому шляхом еквівалентних перетворень приведемо СЛАР до потрібного вигляду:
Помножимо 2-й рядок на -2 і додамо до нього 3-й. отримаємо систему:
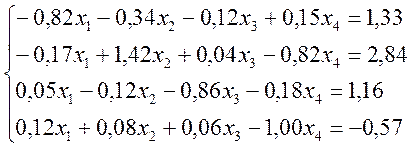
Перевіримо достатню умову збіжності.
Для першого рядка маємо
½ -0,82 ½ > ½-0,34½ + ½-0,12½ +½0,15½ = 0,61 умова виконується.
Для другого рядка маємо
½ 1,42 ½ > ½-0,17½ + ½0,04½ +½-0,82½ = 0,88 умова виконується.
Для третього рядка маємо
½ -0,86 ½ > ½0,05½ + ½-0,12½ +½-0,18½ = 0,35 умова виконується.
Для четвертого рядка маємо
½ -1,00 ½ > ½0,12½ + ½0,08½ +½0,18½ = 0,38 умова виконується.
Використаємо метод Зейделя. Кожне наступне (n+1) наближення розв’язку знаходимо за формулами:
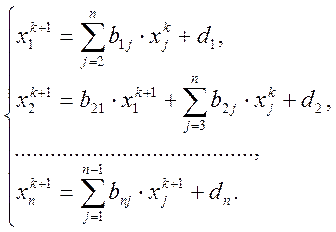
де B=[bij] - квадратна матриця порядку n:
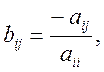
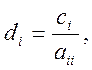
![]() .
.
Обчислення проводимо до тих пір, поки
½ xin+1
– xin ½< e тобто ½ xin+1
– xin ½< 0,0001 для всіх і (![]() )
)
Для обчислення використаємо середовище програмування Turbo Pascal.
program chm2;
uses WinCRT;
var x01, x02, x03, x04, x1, x2, x3, x4 : real;
i : integer;
const e=0.0001;
begin
i := 0;
writeln('x01, x02, x03, x04');
readln (x1, x2, x3, x4);
repeat
x01:=x1;
x02:=x2;
x03:=x3;
x04:=x4;
x1:=(1.33+0.34*x2+0.12*x3-0.15*x4)/(-0.82);
x2:=(2.84+0.17*x1-0.04*x3+0.82*x4)/(1.42);
x3:=(1.16-0.05*x1+0.12*x2+0.18*x4)/(-0.86);
x4:=(-0.57-0.12*x1-0.08*x2-0.06*x3)/(-1);
i := i + 1;
writeln(i,': ','x1=',x1:3:5,' x2=',x2:3:5,' x3=',x3:3:5,' x4=',x4:3:5);
until (abs(x1-x01)<e) and (abs(x2-x02)<e) and (abs(x3-x03)<e) and (abs(x4-x04)<e);
end.
За початкове наближення беремо: х10 = 1; х20 = 1; х30 = 1; х40 = 1.
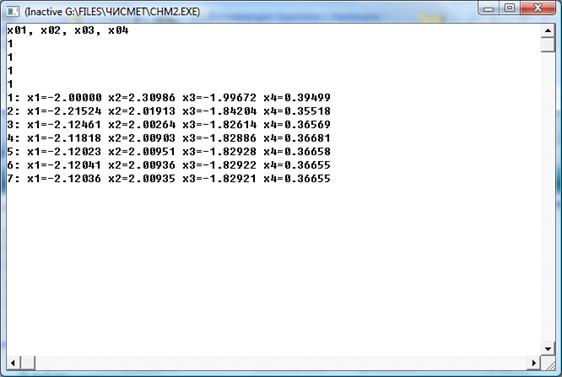
Відповідь: x1=-2,12036, x2=2,200935, x3=-1,82921, x4=0,36655
Визначимо міру обумовленості та оцінимо вплив вхідних даних на результат. Для цього складемо матриці:
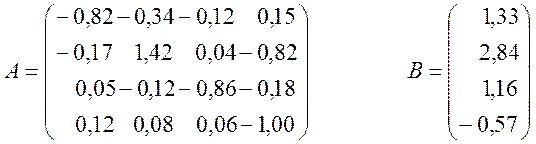
Знайдемо обернену матрицю А-1. Для цього використаємо Mathcad:
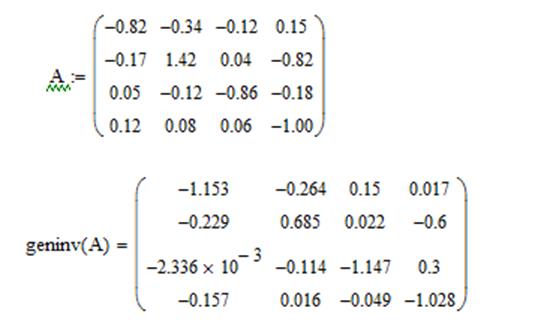
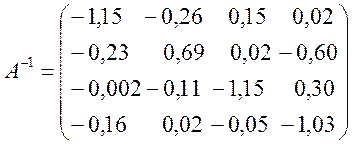
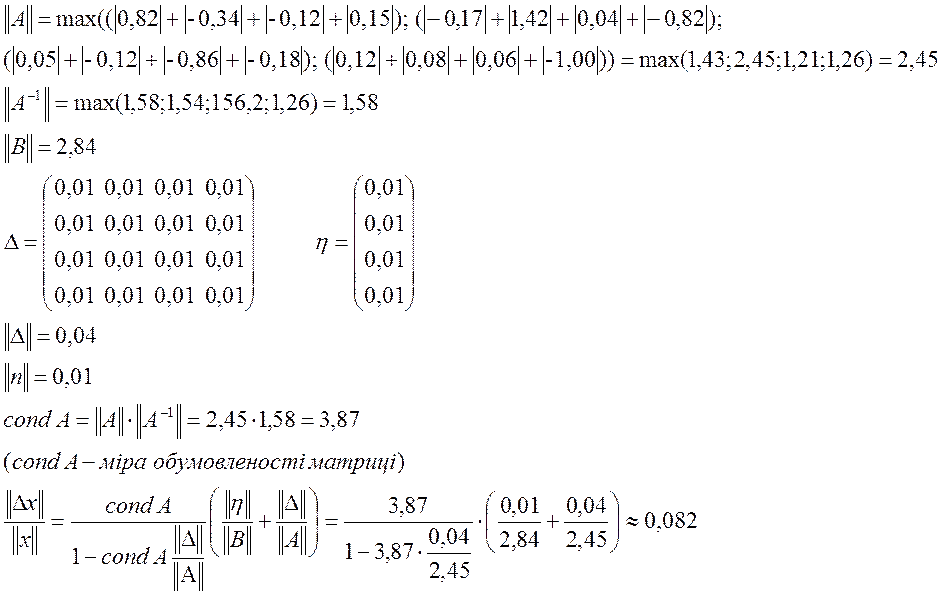
Тобто, похибка вхідних даних складає 8,2%.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.