Розв’язання крайової задачі для ЗДР з точністю 0.0001, використовуючи метод прогнозу і корекції

Використовуючи метод прогнозу і корекції, розв’язати крайову задачу для ЗДР з точністю

5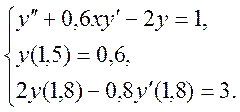   

Підправивши схему Ейлера в середній точці, отримаємо схему прогнозу:

де наближене значення . Однак цю формулу використовувати не можна, так як схема прогнозу нестійка. Тому використовуємо схему корекції:

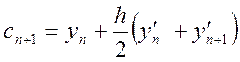
Для оцінки похибки корекції розкладемо в ряд Тейлора в околі точки  корекцію

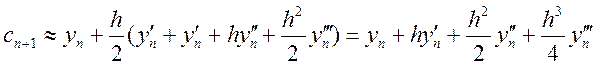
а також саму функцію

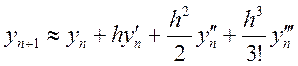
Віднявши перше розкладення від другого, отримаємо:

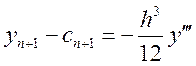 (1)

Ті ж дії виконаємо для оцінки похибки прогнозу:

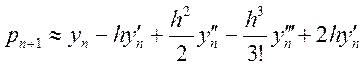
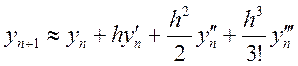
Отримаємо похибку прогнозу:

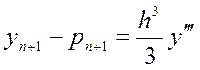 (2)

Точне значення розв’язку лежить між прогнозом и корекцією, так як прогноз наближає розв’язок з недостачею, а корекція – із надлишком. На будь-якому кроці можна оцінити точність розв’язку. Якщо задається значення точності , то .

Якщо (2)-(1), то отримаємо:

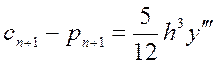
Уточнимо розв’язок, виходячи з формули (1):

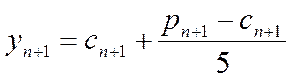
Таким чином, схема прогнозу і корекції буде мати вигляд:

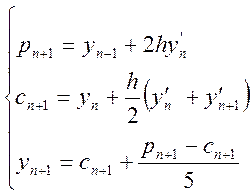
Для зниження порядку вихідного рівняння використовуємо заміни . Оберемо сітку . В результаті отримаємо систему:

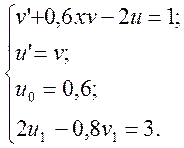
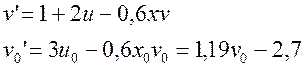
 и  знайдемо за допомогою розкладення в ряд Тейлора:

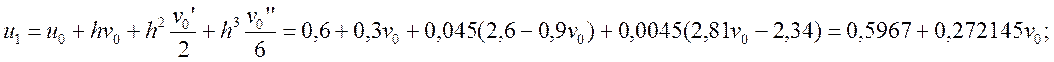
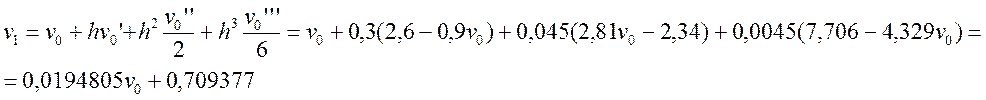Підставивши отримані значення у вихідне рівняння, знайдемо :

Система, що буде розв’язуватися програмно:

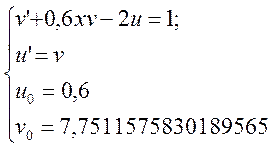
Запрограмуємо дану задачу в середовищі програмування Turbo Pascal:

program lr8;

type mas=array[1..1000] of real;

  var a,b,x,h,ma:real;

    i,n:integer;

    u,u1,v,v1:mas;

    k1,k2,k3,k4:real;

    p1,p2,p3,p4:real;

  const

 eps=0.0001;

  Function Fun1(x,u,v:real):real;

    begin

      Fun1:=v;

    end;

  Function Fun2(x,u,v:real):real;

    begin

      Fun2:=1+2*u-0.6*v*x;

    end;

 Function max(u,u1,v,v1:mas; n:integer):real;

   var i: integer;

       m1,m2,ma:real;

   begin

     m1:=abs(u1[1]-u[1]);

     for i:=2 to n do

      if abs(u1[i]-u[2*i-1])/15>m1 then m1:=abs(u1[i]-u[2*i-1])/15;

     m2:=abs(v1[1]-v[1]);

     for i:=2 to n do

      if abs(v1[i]-v[2*i-1])/15>m2 then m2:=abs(v1[i]-v[2*i-1])/15;

   if m1>m2 then ma:=m1 else ma:=m2;

   max:=ma;

   end;

begin

   h:=0.05;

   u[1]:=0.6;

   v[1]:=7.75115758301;

   a:=1.5;

   b:=1.8;

   x:=a;

   n:=round((b-a)/h);

   for i:=2 to n do

    begin

     k1:=Fun1(x,u[i-1],v[i-1]);

     p1:=Fun2(x,u[i-1],v[i-1]);

     k2:=Fun1(x+0.5*h,u[i-1]+0.5*h*k1,v[i-1]+h*p1/2);

     p2:=Fun2(x+0.5*h,u[i-1]+0.5*h*k1,v[i-1]+h*p1/2);

     k3:=Fun1(x+0.5*h,u[i-1]+0.5*h*k2,v[i-1]+h*p2/2);

     p3:=Fun2(x+0.5*h,u[i-1]+0.5*h*k2,v[i-1]+h*p2/2);

     k4:=Fun1(x+h,u[i-1]+h*k3,v[i-1]+h*p3);

     p4:=Fun2(x+h,u[i-1]+h*k3,v[i-1]+h*p3);

    u[i]:=u[i-1]+(h/6)*(k1+2*k2+2*k3+k4);

    v[i]:=v[i-1]+(h/6)*(p1+2*p2+2*p3+p4);

    x:=x+h;

    end;

  {-------------}

   repeat

     for i:=1 to n do

     begin

      u1[i]:=u[i];

      v1[i]:=v[i];

     end;

     h:=h/2;

      n:=round((b-a)/h);

      x:=a;

      for i:=2 to n do

    begin

     k1:=Fun1(x,u[i-1],v[i-1]);

     p1:=Fun2(x,u[i-1],v[i-1]);

     k2:=Fun1(x+0.5*h,u[i-1]+0.5*h*k1,v[i-1]+h*p1/2);

     p2:=Fun2(x+0.5*h,u[i-1]+0.5*h*k1,v[i-1]+h*p1/2);

     k3:=Fun1(x+0.5*h,u[i-1]+0.5*h*k2,v[i-1]+h*p2/2);

     p3:=Fun2(x+0.5*h,u[i-1]+0.5*h*k2,v[i-1]+h*p2/2);

     k4:=Fun1(x+h,u[i-1]+h*k3,v[i-1]+h*p3);

     p4:=Fun2(x+h,u[i-1]+h*k3,v[i-1]+h*p3);

    u[i]:=u[i-1]+(h/6)*(k1+2*k2+2*k3+k4);

    v[i]:=v[i-1]+(h/6)*(p1+2*p2+2*p3+p4);

     x:=x+h;

    end;

  until Max(u,u1,v,v1,n)<eps;

  ma:=Max(u,u1,v,v1,n);

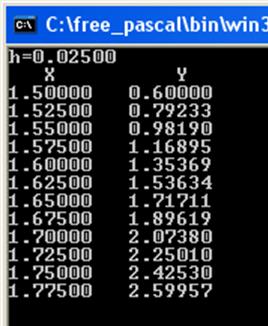
  writeln('h=',h:1:5);

    writeln('   X          Y');

  x:=a;

  for i:=1 to n do

  begin

     writeln(x:7:5,'   ',u[i]:7:5);

     x:=x+h;

     end;

end.