Лабораторна робота №4. Варіант 10. Татарченко Аліна
Пункт # 1 – Умова задачі
Для функції y=f(x), що задана таблично, побудувати інтерполяційний многочлен і сплайн. Обчислити в заданій точці x* значення функції і встановити, якою з інтерполюючих функцій доцільніше скористатися.
|
Значення |
х* |
|
|
x |
0 1 2 3 4 |
3,6 |
|
y |
2 12 19 20 70 |
Пункт #2 – Математичне обґрунтування алгоритму розв’язання
1. Наближувати задану функцію будемо по другій інтерполяційній формулі Ньютона:
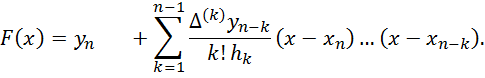
Ця формула називається формулою інтерполювання
назат, що використовується в тому разі, коли інтерполяційна точка розташована в
таблиці ближче до ![]() , ніж до
, ніж до ![]() .
.
Формулу Ньютона записано через скінченні
різниці, а не через розділені, тому що аргументи заданої таблично функції
розташовані на рівномірній сітці: ![]()
Скінченні різниці розраховуються за формулою:
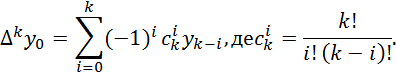
Складемо таблицю скінченних різниць:
|
|
|
|
|
|
|
2 |
||||
|
10 |
||||
|
12 |
-3 |
|||
|
7 |
-3 |
|||
|
19 |
-6 |
58 |
||
|
1 |
55 |
|||
|
20 |
49 |
|||
|
50 |
||||
|
70 |
Отже, дана функція не є поліномом. Дана функція сплайн.
Підставивши значення кінцевих різниць в формулу Ньютона, отримаємо поліном, що інтерполює задану таблично функцію:
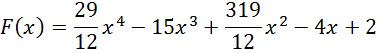
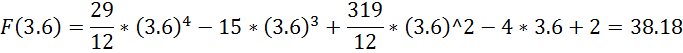
2. Кубічні сплайни.
Ці сплайни моделюють старий креслярський
механічний пристрій, який представляє собою гнучку рейку, що закріплюється в
певних точках (вузлах інтерполяції). Таким чином ця рейка або механічний сплайн
набували форми з найменшою потенційною енергією. Ця умова виглядає математично:
![]() . Якщо при цьому сплайн
не руйнується, то функція і її похідні повинні бути неперервними на [a,b]. Значить, на
проміжку між кожною парою сусідніх вузлів інтерполяційна функція являє собою
многочлен третього степеню, який зручно записати в такому вигляді:
. Якщо при цьому сплайн
не руйнується, то функція і її похідні повинні бути неперервними на [a,b]. Значить, на
проміжку між кожною парою сусідніх вузлів інтерполяційна функція являє собою
многочлен третього степеню, який зручно записати в такому вигляді: ![]() (*). Коефіцієнти
многочлена на кожному інтервалі визначаються з умов у вузлах. Очевидно, що у
вузлах многочлен повинен приймати табличні значення функції:
(*). Коефіцієнти
многочлена на кожному інтервалі визначаються з умов у вузлах. Очевидно, що у
вузлах многочлен повинен приймати табличні значення функції: ![]() ,
, ![]() (1),
(1), ![]() ,
, ![]() (2). Число цих рівнянь вдвічі менше за число невідомих коефіцієнтів, тому
для визначеності задачі необхідні додаткові умови. Для їх отримання обчислимо
першу і другу похідні многочлена (*):
(2). Число цих рівнянь вдвічі менше за число невідомих коефіцієнтів, тому
для визначеності задачі необхідні додаткові умови. Для їх отримання обчислимо
першу і другу похідні многочлена (*): ![]() ,
, ![]() при
при ![]() , і будемо вимагати
неперервності цих похідних (тобто гладкості лінійки) в усіх точках, включаючи
вузли. Прирівнявши у внутрішньому вузлі
, і будемо вимагати
неперервності цих похідних (тобто гладкості лінійки) в усіх точках, включаючи
вузли. Прирівнявши у внутрішньому вузлі ![]() праві та ліві границі похідних, отримаємо
праві та ліві границі похідних, отримаємо ![]() ,
, ![]() , (3)
, (3)![]() ,
, ![]() (4). Невистачаючі дві умови звичайно отримують із природного припущення
про нульову кривизну графіка на кінцях:
(4). Невистачаючі дві умови звичайно отримують із природного припущення
про нульову кривизну графіка на кінцях: 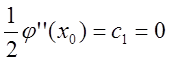 ,
, 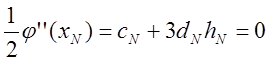 (5), що відповідає вільно опущеним кінцям лінійки.
(5), що відповідає вільно опущеним кінцям лінійки.
Але якщо є додаткові відомості про асимптотику функції, то можна записати інші крайові умови.
[0;1] ![]()
[1;2] ![]()
[2;3] ![]()
[3;4] ![]()
Підставляючи у формули (1) – (5) дані значення, отримаємо систему рівнянь (hi=const=1):
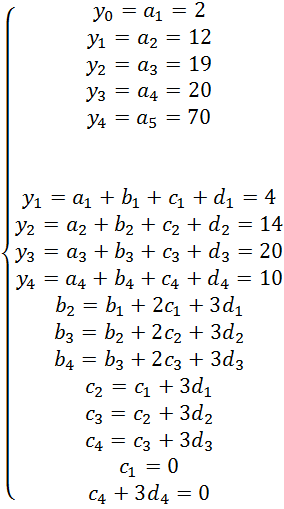
Спростивши, отримаємо:
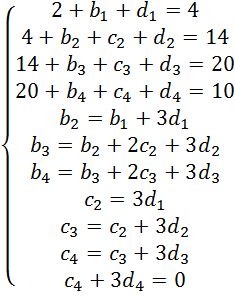
(Для програмної реалізації)Якщо 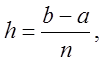
![]() (
(![]() ),
), ![]() , то
кубічний сплайн на цьому відрізку
, то
кубічний сплайн на цьому відрізку
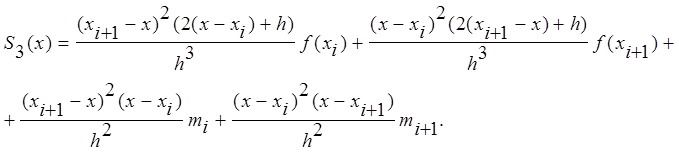
Де коефіцієнти обраховуються за формулою:
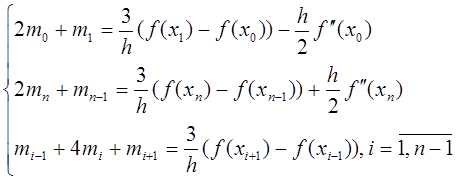
Оскільки ми не маємо
інформації про![]() то можемо використати природні
граничні (крайові) умови
то можемо використати природні
граничні (крайові) умови![]() .
.
Пункт # 3 – Програмна реалізація
#include<iostream>
#include<math.h>
#define N 5
voidzeidel(float A[N][N],float B[N],floateps,float X1[N])
{
float C[N][N],D[N],X0[N],max;
inti,j;
for(i=0;i<N;i++)
for(j=0;j<N;j++)
if (i!=j)
C[i][j]=-A[i][j]/A[i][i];
else
C[i][j]=0;
for(i=0;i<N;i++)
D[i]=B[i]/A[i][i];
for(i=0;i<N;i++)
X0[i]=0;
max=1;
while(max>=eps){
max=0;
for(i=0;i<N;i++)
{X1[i]=C[i][0]*X0[0]+C[i][1]*X0[1]+C[i][2]*X0[2]+C[i][3]*X0[3]+C[i][4]*X0[4]+D[i];
if (fabs(X1[i]-X0[i])>max) max=fabs(X1[i]-X0[i]);
X0[i]=X1[i]; }
}
}
float spline(float* x,float *y,float *m,float X)
{
intr,i;
float h;
for(i=0;i<5;i++)
if(X>x[i]&&X<x[i+1])
break;
h=x[1]-x[0];
return(pow(x[i+1]-X,2)*(2*(X-x[i])+1)*y[i]/(h*h*h)+
pow((X-x[i]),2)*(2*(x[i+1]-X)+1)*y[i+1]/(h*h*h)+
pow(x[i+1]-X,2)*(X-x[i])*m[i]/(h*h)+
pow(X-x[i],2)*(X-x[i+1])*m[i+1]/(h*h));
}
float newton(float *x,float *y,float x0)
{floatdy[4],d2y[3],d3y[2],d4y;
int i;
for(i=0;i<4;i++)
dy[i]=y[i+1]-y[i];
for(i=0;i<3;i++)
d2y[i]=dy[i+1]-dy[i];
for(i=0;i<2;i++)
d3y[i]=d2y[i+1]-d2y[i];
d4y=d3y[1]-d3y[0];
return y[0]+dy[0]*(x0-x[0])+d2y[0]*(x0-x[0])*(x0-x[1])/2+d3y[0]*(x0-x[0])*(x0-x[1])*(x0-x[2])/6+d4y*(x0-x[0])*(x0-x[1])*(x0-x[2])*(x0-x[3])/24;
}
void main()
{
float A[N][N]={2,1,0,0,0,1,4,1,0,0,0,1,4,1,0,0,0,1,4,1,0,0,0,1,2},
B[N],m[N],eps=0.0001,X[N],Y[N],x0,h,sx;
inti,j;
for(i=0;i<N;i++)
{printf("Vvedite X[%i]=",i);
scanf("%f",&X[i]);}
for(i=0;i<N;i++)
{printf("Vvedite Y[%i]=",i);
scanf("%f",&Y[i]);}
printf("Vvedite X0");
scanf("%f",&x0);
h=X[1]-X[0];
B[0]=(3/h)*(Y[1]-Y[0]);
B[4]=(3/h)*(Y[4]-Y[3]);
B[1]=(3/h)*(Y[2]-Y[0]);
B[2]=(3/h)*(Y[3]-Y[1]);
B[3]=(3/h)*(Y[4]-Y[2]);
zeidel(A,B,eps,m);
printf("\n\nspline %6.4f\nlagrange %6.4f",spline(X,Y,m,x0),newton(X,Y,x0));
system("pause");}
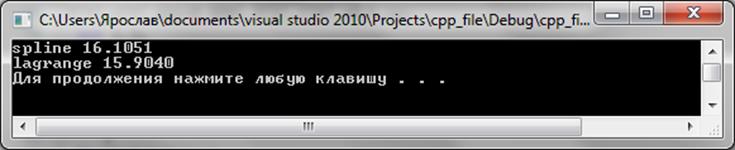
Пункт # 4 – Пакетна реалізація
Пакетна реалізація здійснена за допомогою програмиMaple.
>![]()
![]()
![]()
Знайдемо розв'язок системи:
>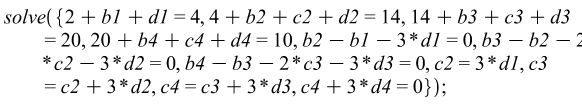
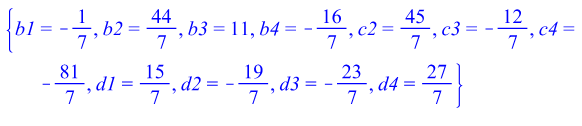
Отже, ми отримали такі кубічні сплайни:
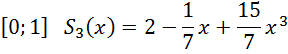
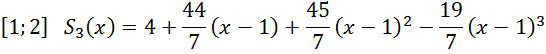
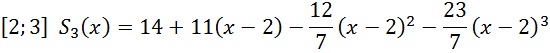
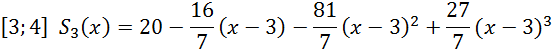
Обчислимо
значення ![]()
![]() 16.105
16.105
Пункт # 5 – Висновок
Доцільніше було б скористатися для побудови інтерполяційного многочлена кубічним сплайном, тому що у методі інтерполювання за Ньютоном при збільшенні кількості вузлів процес обчислення скінченних та поділених різниць стає все більш обчислювально нестійким – похибка визначення скінченних різниць великого порядку різко зростає зі збільшенням порядку скінченної різниці. Тому метод Ньютона може бути застосований лише для невеликої кількості вузлів.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.