Метричні простори. Абсолютна величина і норма матриці. Псевдокод

Додатки

1 Метричні простори

Оскільки розв’язками рівнянь математичної моделі можуть бути об'єкти різного походження: числа, упорядковані набори чисел, вектори, функції (при розгляді диференціальних і інтегральних рівнянь), то при обґрунтуванні методів реалізації математичних моделей різноманітних задач доцільно одержати аналоги відповідних теорем для відображень множин довільної природи. Це призводить до необхідності розгляду множин, на яких уведена відстань. Такі множини називаються метричними просторами. Дамо точні визначення.

Нехай X — непорожня множина і кожній парі елементів х, у з множини поставлено у відповідність невід’ємне число r(х, у) з такими трьома властивостями:

1) r(х, у) = 0 тоді і тільки тоді, коли х = у;

2) r(х, у) = r(у, х) (властивість симетрії);

3) r(х, у) = r(x, z) +r(z, у) (нерівність трикутника).

Ці властивості виконуються для всіх х, у, z з X. Число r(х, у) називають відстанню між елементами х та у. Множина X із заданою на ньому відстанню називається метричним простором. Розглянемо кілька прикладів метричних просторів.

Приклад 1 На множині R дійсних чисел відстань визначається, як правило,: r(х, у)=|х-у|, х,у є R. На R можна розглядати й інші відстані. Наприклад,  d(x, у)=|arctgx-arctgy|,   х, у є R.

Приклад 2 На множини Rⁿ упорядкованих наборів n дійсних чисел можна розглянути такі три відстані:

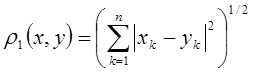(евклідова відстань);

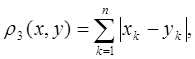
де х = (х₁,..., х_n), у = (у₁,..., у_n) — довільна пара наборів дійсних чисел.

Цей метричний простір, як правидо, використовується при вивченні систем рівнянь з декількома невідомими.

Приклад 3 Нехай f[а, b] — множина неперервних функцій на відрізку [а, b]. Тоді формула

визначає відстань між функціями на [а, b].

У будь-якому метричному просторі Х з відстанню r можна визначити поняття збіжної фундаментальної послідовності.

Послідовність {х_n} = (х₁, х₂, ...) елементів метричного простору X називається збіжною до елемента х₀ є X, якщо для кожного e>0 можна знайти таке натуральне число N, що r(х_n, х₀)< e для всіх n > N. Елемент х₀ називається границею послідовності {х_n}, тобто  .

Послідовність {х_n} елементів з X називається фундаментальною (чи послідовністю Коші), якщо для кожного e>0 існує таке натуральне N, що r(х_n, х_m)< e  при всіх n, m > N.

Метричний простір X називається повним, якщо будь-яка фундаментальна послідовність з X збігається до деякого елемента з X.

В усіх розглянутих тут прикладах метричних просторів вони є повними, крім метричного простору R з відстанню d.

2 Абсолютна величина і норма матриці

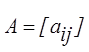Нерівність  між матрицями  й  одного типу означає,  що  

У такому сенсі не всякі дві матриці можна порівняти між собою.

  За абсолютну величину (модуль) матриці  будемо вважати матрицю

де  – модулі елементів матриці .

  Якщо  і  – матриці, для яких операції  і  мають сенс, то:

  а)

  б)

  в) , (  - число).

За норму матриці  вважаємо дійсне число , що задовольняє  умови:

а) причому  тоді і тільки тоді, коли =0;

б) (  - число ) і, зокрема, ;

в) ;

г)

( і  - матриці, для яких відповідні операції мають сенс).

Відзначимо ще одну важливу нерівність між нормами матриць  і  одного типу. Застосовуючи умову в), будемо мати

Звідси

Аналогічно

Отже,

  Назвемо норму канонічною, якщо додатково виконані умови:

  д) якщо  то

причому для скалярної матриці  маємо

  е) з нерівності  (А і В – матриці ) випливає нерівність

Зокрема, .

Надалі для матриці   довільного типу ми будемо розглядати головним чином три канонічні норми, що легко обчислюються:

  1) 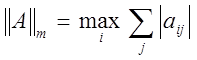   (m – норма);

  2) 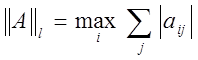    ( - норма);

  3) 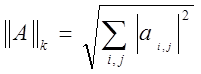 ( - норма).

  Приклад. Нехай

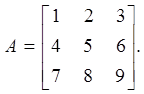
Маємо:

Нехай маємо послідовність матриць  одного типу

За границю послідовності матриць  вважається матриця

                                   

  Послідовність матриць, що має границю, є збіжною.

Лема 1 Для збіжності послідовності матриць  (к=1,2,…) до матриці А необхідно і достатньо, щоб

                                        при     ,            

де  - будь-яка конічна норма матриці А. При цьому

Лема 2 Для збіжності послідовності матриць    необхідно і достатньо, щоб був виконаний узагальнений критерій Коші, а саме: для будь-якого  повинен існувати такий номер  , що при

, де  - будь-яка канонічна норма.

3 Псевдокод

Псевдокод нагадує існуючі мови програмування (такі, як Pascal або C) та на відміну від них є простішим і більш компактним. Крім того, у псевдокоді інколи можна записувати дії алгоритму своїми словами, якщо так ясніше.

На відміну від конкретної мови програмування псевдокод дозволяє опустити несуттєві технічні подробиці, такі як обробка помилок, що необхідно у реальній програмі але заважає вивченню алгоритмів.