Математический анализ: Курс лекций (часть вторая "Интегральное исчисление функции одной переменной")

1. Неопределенный интеграл

1.1. Первообразная и неопределенный интеграл

Определение: Функция  называется первообразной функцией (просто первообразной) функции  на интервале  если  .

Аналогично определяется понятие первообразной на любом другом  промежутке.

Примеры:

1. 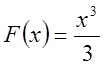 является первообразной функции  на .

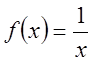2.  является первообразной функции  на .

Теорема: Две дифференцируемые на промежутке  функции  и являются первообразными одной и той же функции  тогда и только тогда, когда они отличаются на постоянную.

, , .

Доказательство:

Если  первообразная  т.е.  , то и  также является первообразной функции , так как  .

Если  и  первообразные , то  и .

В силу следствия 1 из теоремы Лагранжа  на  .

€

Определение: Пусть функция  определена на некотором промежутке. Совокупность всех ее первообразных на этом промежутке называется неопределенным интегралом от функции  и обозначается

,

где

- подинтегральная функция;

- подинтегральное выражение.

Если  какая - либо первообразная  на рассматриваемом  промежутке, то пишут 

, .

Очевидно,, поэтому по определению полагают

.

1.2. Основные свойства неопределенного интеграла

1⁰.  (следует непосредственно из определения);

2⁰.  (следует непосредственно из определения).

3⁰. Если  и  имеют на промежутке первообразные, то и функция  также имеет на  первообразную, причем

.

4⁰. Если  имеет первообразную на промежутке, то функция, также имеет первообразную на , причем при

.

Следствие: (свойство линейности).

,

где  такие, что .

Докажем свойство 3.

Доказательство:

Пусть и  первообразные соответственно  и , т.е.   и .

Рассмотрим функцию. Эта функция является первообразной для функции  , т. к.

 .

Следовательно,

.

С другой стороны,

.

Так как  - произвольные постоянные, то правые части последних равенств совпадают, следовательно, совпадают и их левые части. €

Докажем свойство 4.

Доказательство:

Пусть первообразная   т.е. , . Тогда функция  является первообразной для функции , так как , .

Поэтому

, а .

В силу произвольности постоянных  правые части последних равенств равны, следовательно, равны и левые. €

1.3. Таблица основных неопределенных интегралов

Операция нахождения неопределенного интеграла от данной функции называется интегрированием и является действием обратным дифференцированию.

1. , ;

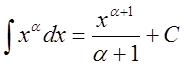2. ,  ;

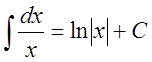3. ,  ;     ;

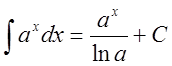4. ;

5. ;

6. ;

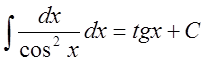7.

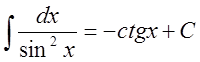
8. ;

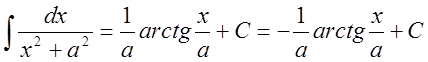9. ;

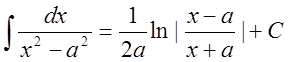10.,  ();

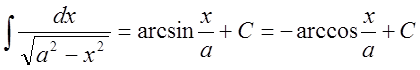11.

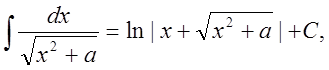
(если, то );

12. ;

13. ;

14. ;

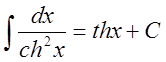15. ;

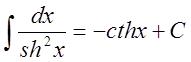 Справедливость этих формул проверяется непосредственным дифференцированием их правых частей.

1.4. Основные методы интегрирования

1.4.1. Метод замены переменной (подстановки)

Теорема: Пусть функции  и  определены соответственно на промежутках  и , причем ; функция  имеет на  первообразную , а функция  дифференцируема на . Тогда функция  на промежутке   имеет первообразную  причем

.

Доказательство:

По условию  .

Вычислим ,    -  первообразная  функции .

Следовательно,

.

С другой стороны,

.

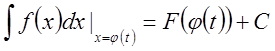Поскольку правые части последних равенств равны, то равны и левые части.

€

Примеры:

1. Найти интеграл .

Решение:

.

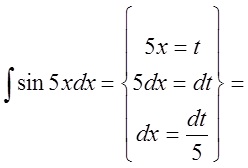
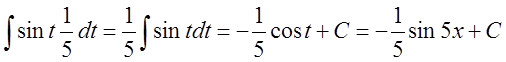2. Найти интеграл .

Решение:

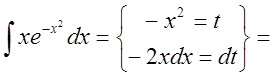
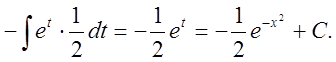
3. Найти интеграл .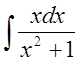

Решение:

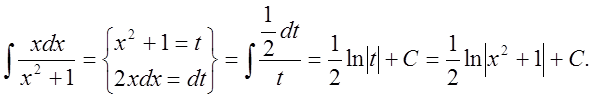
3.1. (Подведение под знак дифференциала)

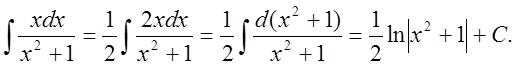
4. Найти интеграл .

Решение:

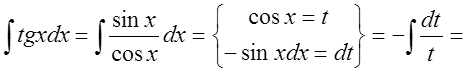
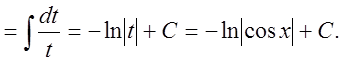
4.1. (Подведение под знак дифференциала)

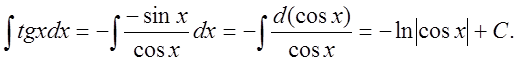
5. Найти интеграл .

Решение:

.

1.4.2. Интегрирование по частям

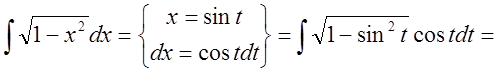
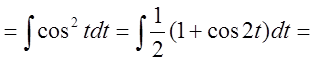
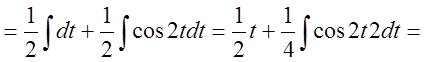
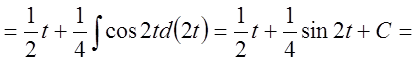
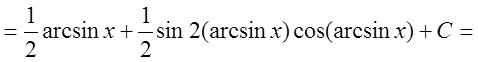
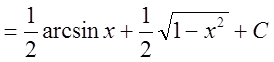Теорема: Пусть функции  и  дифференцируемы на некотором промежутке и на этом промежутке существует интеграл , тогда на нем существует интеграл, причем

.

Доказательство:

Интегрируя последнее равенство, получим

 по условию существует, следовательно, существует и .

 Отнеся постоянную  к интегралу , получим

.

€

Примеры:

1. Найти интеграл .

Решение:

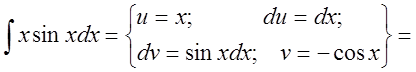
2. Найти интеграл .

Решение:

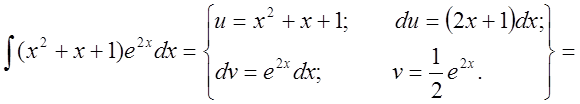
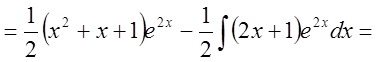
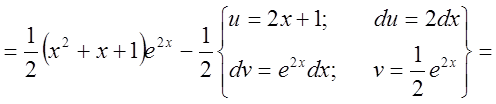
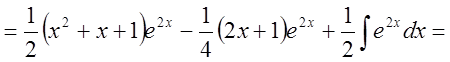
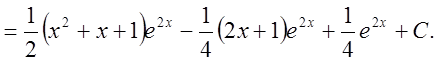
Замечание: Интегрируют по частям, в частности, интегралы:

,,,

,,,

, , , .

1.5. Интегрирование рациональных дробей