Причем, если хотя бы один из интегралов, стоящих в правой части последнего равенства расходится, то расходится и интеграл, стоящий в левой части.
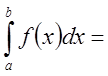 {
{![]() - неограниченна в точках
- неограниченна в точках ![]() и
и ![]() }
}![]()
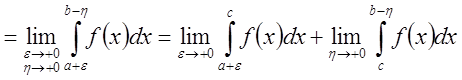 ,
, ![]() .
.
Причем, если хотя бы один из интегралов, стоящих в правой части последнего равенства расходится, то расходится и интеграл, стоящий в левой части.
Примеры:
1.
Исследовать на сходимость интеграл 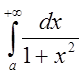 .
.
Решение
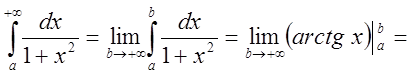
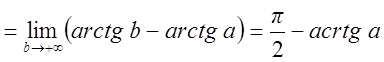 .
.
Интеграл сходится.
2.
Исследовать на сходимость интеграл 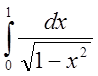 .
.
Решение
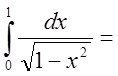 {подынтегральная
функция в т.
{подынтегральная
функция в т. ![]() неограниченна}
неограниченна}![]()
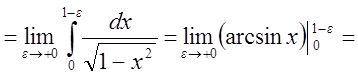
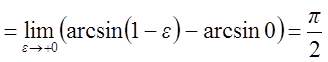 .
.
Интеграл сходится.
3.
Исследовать на сходимость интеграл 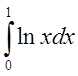 .
.
Решение
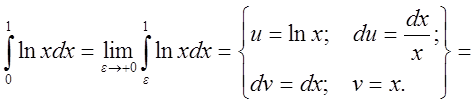

![]()
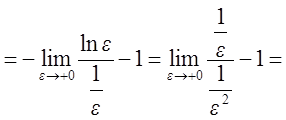
![]() .
.
Интеграл сходится.
4.
Исследовать на сходимость интеграл 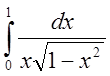 .
.
Решение

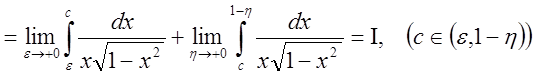 ;
;
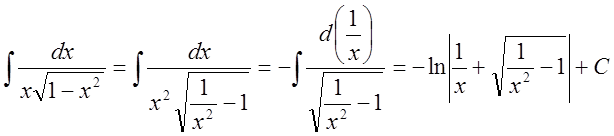 ;
;
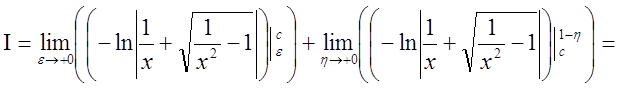
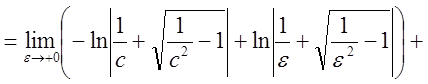
![]() .
.
Интеграл расходится.
5. Основной пример
5.
1. При каких ![]() интеграл
интеграл
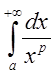
![]() сходится?
сходится?
Решение
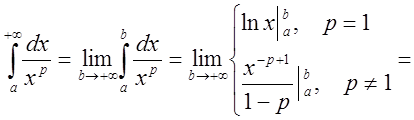
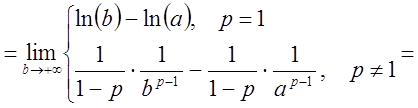
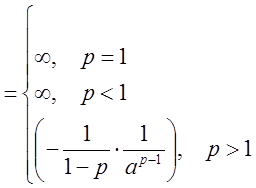 .
.
Имеем:
 .
.
5.
2. При каких ![]() интеграл
интеграл

![]() сходится?
сходится?
Решение
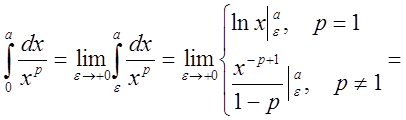
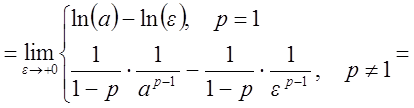
 .
.
Имеем:
 .
.
5. 3. Аналогично можно показать:
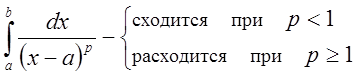 ,
,
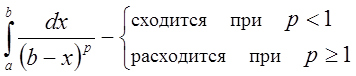 .
.
Теорема:
Пусть функция ![]() определена на промежутке
определена на промежутке ![]() ,
, ![]() и
интегрируема по Риману на
и
интегрируема по Риману на ![]() ,
, ![]() . Для
того чтобы несобственный интеграл
. Для
того чтобы несобственный интеграл 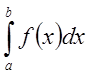 сходился, необходимо и
достаточно, чтобы
сходился, необходимо и
достаточно, чтобы
![]()
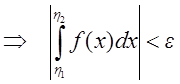 .
.
Доказательство:
Рассмотрим функцию 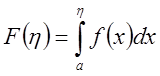 ,
, ![]() . Для того чтобы эта функция имела
предел при
. Для того чтобы эта функция имела
предел при ![]() , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы
![]()
![]() ,
,
(критерий Коши существования предела функции).
Но
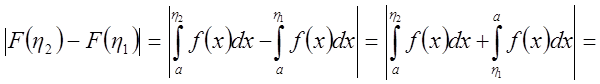
 .
.
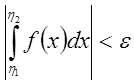 .
.
А
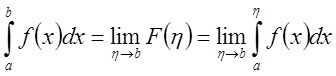 .
.
Теорема: Пусть
функция ![]() неотрицательна на промежутке
неотрицательна на промежутке ![]() ,
, ![]() и интегрируема
на любом отрезке
и интегрируема
на любом отрезке ![]() ,
, ![]() . Для того
чтобы
. Для того
чтобы 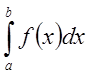 сходился, необходимо и достаточно, чтобы
функция
сходился, необходимо и достаточно, чтобы
функция 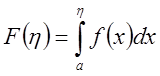 была ограниченна сверху на
была ограниченна сверху на ![]() . В случае выполнения
этого условия
. В случае выполнения
этого условия
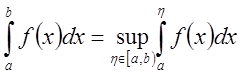 .
.
Доказательство:
Рассмотрим функцию 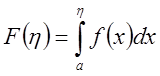 ,
, ![]() . В силу того, что
. В силу того, что ![]() , функция
, функция ![]() не убывает.
не убывает.
В самом деле, если ![]() , то
, то
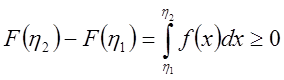 .
.
Несобственный интеграл 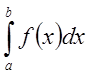 сходится,
тогда и только тогда, когда существует конечный предел
сходится,
тогда и только тогда, когда существует конечный предел
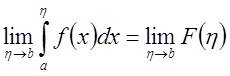 ,
,
а
последний существует тогда и только тогда, когда функция ![]() ограничена сверху, (из теоремы о пределе
монотонной функции) и при этом
ограничена сверху, (из теоремы о пределе
монотонной функции) и при этом
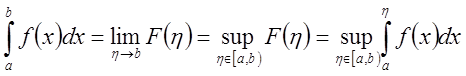 .
.
Признак сравнения
Теорема:
Пусть функции ![]() и
и ![]() неотрицательны
на
неотрицательны
на ![]() и интегрируемы на любом отрезке
и интегрируемы на любом отрезке ![]() ,
, ![]() . Пусть
. Пусть
![]()
![]() (в
частности
(в
частности![]() ).
).
Тогда:
1)
если 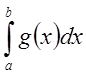 - сходится, то сходится и
- сходится, то сходится и 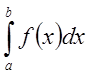 ;
;
2)
если 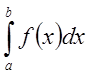 - расходится, то расходится и
- расходится, то расходится и 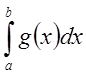 .
.
Доказательство:
1) Пусть 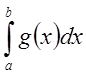 - сходится, тогда по доказанной выше теореме
- сходится, тогда по доказанной выше теореме
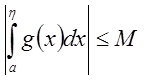 ,
, ![]() .
.
Из ![]() следует, что
следует, что ![]()
![]() выполняется
неравенство
выполняется
неравенство ![]() . Из
. Из 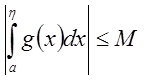 следует,
что
следует,
что 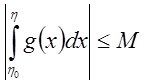 .
.
Следовательно, 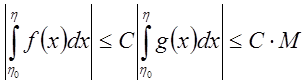 .
.
По доказанной
выше теореме 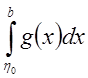 , а, следовательно, и
, а, следовательно, и 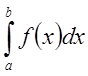 - сходятся.
- сходятся.
2) Если 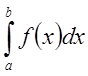 - расходится, то очевидно расходится и
интеграл
- расходится, то очевидно расходится и
интеграл 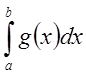 , так как в противном случае по
доказанному
, так как в противном случае по
доказанному 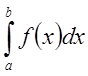 - сходился бы.
- сходился бы.
Следствие: (предельная форма признака сравнения)
Пусть функции ![]() и
и ![]() неотрицательны на
неотрицательны на ![]() и
интегрируемы на любом отрезке
и
интегрируемы на любом отрезке ![]() ,
, ![]() ,
, ![]()
![]() и существует
и существует 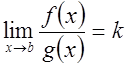 .
.
Тогда:
1) Если ![]() , то из сходимости
, то из сходимости  следует сходимость
следует сходимость 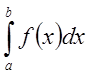 .
.
2) Если ![]() , то из расходимости
, то из расходимости  следует расходимость
следует расходимость 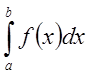 .
.
В частности если ![]() -
число отличное от нуля, то интегралы
-
число отличное от нуля, то интегралы 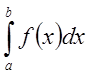 и
и 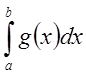 - сходятся или расходятся одновременно.
- сходятся или расходятся одновременно.
Доказательство:
1) Пусть ![]() . Тогда из
. Тогда из 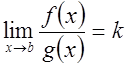
![]()
![]()
![]()
![]()
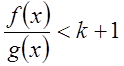 , т.е.
, т.е. ![]() . Это
означает, что
. Это
означает, что ![]()
![]() , и
утверждение 1) следствия следует из 1) признака сравнения.
, и
утверждение 1) следствия следует из 1) признака сравнения.
2)
Пусть ![]() . Тогда из
. Тогда из 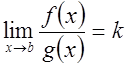
![]()
![]()
![]()
![]()
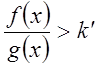 или
или 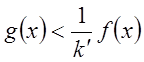 . Это
означает, что
. Это
означает, что ![]()
![]() , и
утверждение 2) следует из 2) признака сравнения.
, и
утверждение 2) следует из 2) признака сравнения.
Примеры:
1.
Исследовать на сходимость интеграл 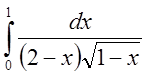 .
.
Решение
 сравним с
сравним с 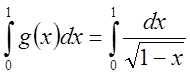 .
.
Известно, что 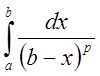 сходится при
сходится при ![]() и
расходится при
и
расходится при ![]() .
.
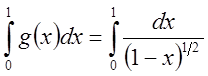 - сходится т.к.
- сходится т.к. 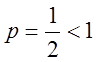 .
.
Поскольку 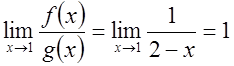 , то по следствию из признака сравнения
, то по следствию из признака сравнения
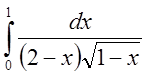 - сходится.
- сходится.
2.
Исследовать на сходимость интеграл 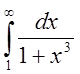 .
.
Решение
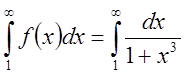 сравним с
сравним с 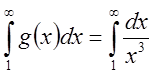 .
.
Известно, что 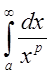 сходится при
сходится при ![]() и
расходится при
и
расходится при ![]() .
.
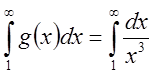 - сходится, т.к.
- сходится, т.к. ![]() .
.
Поскольку  , то по следствию из признака сравнения
, то по следствию из признака сравнения 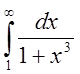 - сходится.
- сходится.
3.
Определить, при каких ![]() интеграл
интеграл 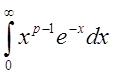 сходится,
а при каких - расходится.
сходится,
а при каких - расходится.
Решение
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.