Математический анализ: Курс лекций (часть вторая "Интегральное исчисление функции одной переменной"), страница 16

1.6. Интегрирование тригонометрических функций. 14

1.6.1. Интегралы вида .................................. 14

1.7. Интегралы от иррациональных функций. 16

1.7.1. Интегралы вида 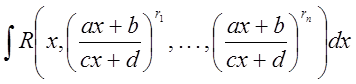...................................................................... 17

1.7.2. Интегралы вида ............................................ 18

1.7.3. Интегрирование дифференциальных биномов. 20

2. Интеграл Римана (определенный интеграл) 22

2.1. Разбиение отрезка. 22

2.2. Интегральные суммы Римана. 23

2.3. Верхние и нижние интегральные суммы (суммы Дарбу) 24

2.4. Свойства сумм Дарбу. 25

2.5. Критерии интегрируемости функции. 27

2.6. Колебания функции. 28

2.7. Классы интегрируемых функций. 29

2.8. Множество меры ноль по Жордану и Лебегу. Критерий  интегрируемости Лебега. 30

2.9. Свойства определенного интеграла. 31

2.10. Первая теорема о среднем.. 36

2.11. Интеграл  как функция переменного верхнего предела. 37

2.12 Формулы интегрирования по частям и замены переменной в определенном интеграле. 40

2.12.1. Формула интегрирования по частям в определенном интеграле. 40

2.12.2. Замена переменной в определенном интеграле. 40

2.13. Остаточный член  формулы Тейлора в интегральной форме. 43

2.14. Вторая теорема о среднем.. 44

2.15. Геометрические и физические приложения определенных интегралов. 45

2.15.1. Вычисление длины кривой. 45

2.15.2. Вычисление площадей плоских фигур. 49

2.15.3. Площадь криволинейной трапеции. 51

2.15.4. Площадь криволинейного сектора. 53

2.15.5. Вычисление объемов тел. 55

2.15.6. Вычисление объема тела по известным площадям его поперечных сечений. 56

2.15.7.  Объём тела вращения. 57

2.15.8. Площадь поверхности вращения. 58

2.15.9 Физические приложения интегралов. 58

2.15.10. Статические моменты и центр масс кривой. 59

2.15.11. Первая теорема Гульдина. 60

2.15.12. Статические моменты и центр масс плоской фигуры.. 61

2.15.13.  Вторая теорема Гульдина. 62

3. Несобственные интегралы.. 63

3.1. Критерий Коши сходимости несобственных интегралов. 66

3.2. Признаки сходимости несобственных интегралов. 67

3.2.1. Сходимость интегралов от  неотрицательных функций. 67

3.2.2. Сходимость интегралов от  знаконеопределенных функций. 70

3.3. Абсолютно  сходящиеся интегралы.. 72

3.4. Главные значения несобственных интегралов. 73

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1. Дороговцев А.Я. Математический анализ. Справочное пособие. К.: «Вища школа», 1985 г.
2. Ильин В.А., Позняк Э.Г. Основы математического анализа. Часть I. Часть II. М.: «Наука», 1980 г.
3. Ильин В.А., Садовничий В.А., Математический анализ. М.: «Наука», 1979 г.
4. Кудрявцев Л.Д. Курс математического анализа. Т.1, Т.2, Т.3. М.: «Высшая школа», 1988 г.
5. Карташев А.П., Рождественский Д.Л. Математический анализ. М.: «Наука», 1984 г.
6. Рудин У. Основы математического анализа. М.: «Мир», 1966 г.
7. Соболев В.И. Лекции по дополнительным главам математического анализа. М.: «Наука», 1968 г.
8. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т.1, Т.2, Т.3. М.: «Наука», 1966 г.
9. Шилов Г.Е. Математический анализ функции одного переменного. М.: «Наука», 1969 г.

АРЛИНСКИЙ Юрий Моисеевич,

КУЧМА Владимир Яковлевич

МАТЕМАТИЧЕСКИЙ АНАЛИЗ

Курс лекций

(часть вторая)

Подписано в печать             ____________

Формат Бумага полиграф. Гарнитура Times.

Печать офсетная. Усл. Печ.     Уч. Изд. Л. 

Тираж  100  экз. Изд. №       Заказ №     Цена договорная

Издательство Восточноукраинского национального университета им. В Даля

91034,г. Луганск, кв Молодежный, 20а

Адрес издательства:91034,г. Луганск, кв Молодежный, 20а

Телефон: 8 (0642) 46-13-64

E-mail: uni@snu.edu.ua.

http://snu.edu.ua

Отпечатано в ООО ’’СЦ’’ЧИП’’,г.Луганск