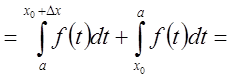 {по свойству аддитивности}
{по свойству аддитивности}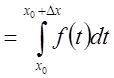 .
.
Так
как![]() , то она ограничена на
, то она ограничена на ![]() ,
,
то есть![]() ,
, ![]() .
.
Имеем
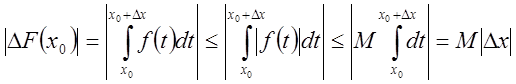 .
.
Очевидно,
![]() , т.е.
, т.е. ![]() непрерывна
в точке
непрерывна
в точке ![]() .
.
Так
как ![]() - произвольная точка
- произвольная точка ![]() , то
, то ![]() непрерывна
на
непрерывна
на ![]() .
.
Теорема
2: Если ![]() и непрерывна в точке
и непрерывна в точке![]() , то функция
, то функция 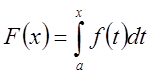 –
дифференцируема в точке
–
дифференцируема в точке ![]() и
и ![]() .
.
Доказательство:
Покажем,
что 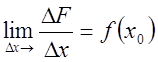 ,
,
где ![]() ,
,
![]() .
.
Очевидно, 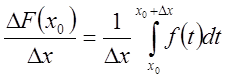 и
и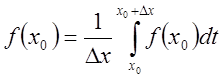 .
.
Тогда
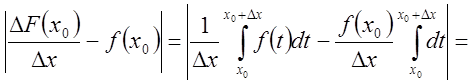
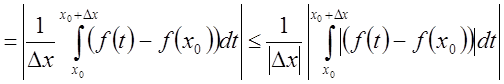 .
.
Пусть задано
произвольное ![]() . В силу непрерывности функции
. В силу непрерывности функции ![]() в точке
в точке ![]()
![]() :
: ![]() и
и ![]()
![]()
![]() .
Выберем
.
Выберем ![]() .
.
Тогда
![]() имеем
имеем ![]() и,
следовательно,
и,
следовательно,
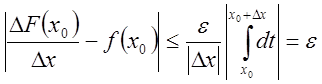 .
.
Это
означает, что 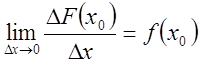 , т.е.
, т.е. ![]() .
.
Следствие
1: Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , то функция
, то функция 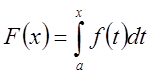 является
первообразной функции
является
первообразной функции ![]() на
на![]() .
.
Доказательство:
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , то она интегрируема на нем. Тогда по
доказанной теореме
, то она интегрируема на нем. Тогда по
доказанной теореме ![]() ,
, ![]() и по
определению функция
и по
определению функция ![]() является первообразной
является первообразной ![]() на
на ![]() .
.
Следствие
2: (Формула Ньютона - Лейбница).Если ![]() - непрерывна на
- непрерывна на ![]() и
и
![]() - какая-либо ее первообразная на этом
отрезке, то
- какая-либо ее первообразная на этом
отрезке, то 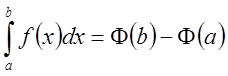 .
.
Доказательство:
Пусть 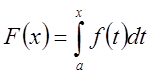 . Согласно теореме 2 функция
. Согласно теореме 2 функция ![]() является первообразной
является первообразной ![]() на
на ![]() .
Следовательно,
.
Следовательно, ![]() и
и ![]() - две
первообразные одной и той же функции,
- две
первообразные одной и той же функции, ![]() ,
, ![]() ,
, ![]() , т.е.
, т.е. 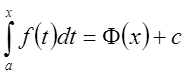 ,
, ![]() .
.
При
![]()
![]()
![]()
![]()
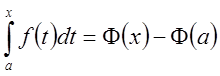 .
.
При
![]()
![]()
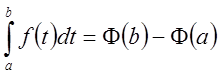 .
.
Для удобства записи полагают
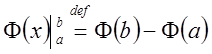
и тогда пишут
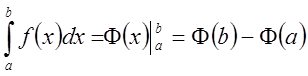 .
.
Пример
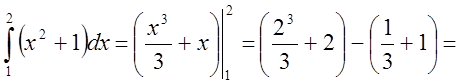
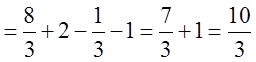 .
.
Теорема: Если функции ![]() и
и ![]() непрерывно дифференцируемы на отрезке
непрерывно дифференцируемы на отрезке ![]() , то справедливо равенство:
, то справедливо равенство:
 .
.
Эта формула называется формулой интегрирования по частям в определенном интеграле.
Доказательство:
Имеем
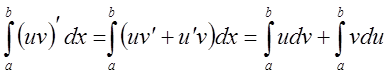 .
.Все написанные интегралы существуют, так как подынтегральные функции непрерывны. Согласно формуле Ньютона – Лейбница имеем:
 .
.
Так как левые части последних двух равенств равны, то равны и правые части, откуда получаем:
 .
.
Теорема: Пусть
1) функция ![]() непрерывная на отрезке
непрерывная на отрезке ![]() ;
;
2) функция ![]() определена и непрерывна со своей производной
определена и непрерывна со своей производной
![]() на отрезке
на отрезке ![]() , причем
, причем
![]() ,
, ![]() ,
, ![]() .
.
Тогда имеет место равенство
 .
(*)
.
(*)
Эта формула называется формулой замены переменной в определенном интеграле или формулой интегрирования подстановкой.
Доказательство:
Заметим,
что ![]() определена на множестве значений функции
определена на множестве значений функции ![]() , поэтому сложная функция
, поэтому сложная функция ![]() имеет смысл
имеет смысл ![]() .
.
Так как подынтегральные функции в обеих частях равенства (*) непрерывны, то оба интеграла существуют.
Пусть
![]() какая либо первообразная функции
какая либо первообразная функции ![]() на
на![]() . Тогда для
. Тогда для ![]() имеет
смысл сложная функция
имеет
смысл сложная функция ![]() , которая является первообразной
для функции
, которая является первообразной
для функции ![]() . По формуле Ньютона – Лейбница
. По формуле Ньютона – Лейбница  ,
,
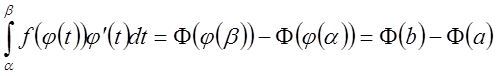 .
.
Из этих равенств следует формула (*).
Замечание 1: При доказательстве теоремы производные всех функций (в том числе сложной) на концах отрезков понимались как соответствующие односторонние производные.
Замечание 2: В формуле (*) левая и правая части есть одно и то же число. Поэтому при замене переменной в определенном интеграле нет необходимости после интегрирования возвращаться к исходной переменной.
Следствие
1: Пусть ![]() ,
,![]() .
.
Тогда:
1)
 , если
, если ![]() -
четная;
-
четная;
2)
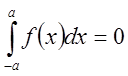 , если
, если ![]() -
нечетная .
-
нечетная .
Доказательство:
Докажем утверждение 2).
Пусть ![]() - нечетная функция на
- нечетная функция на ![]() .
.
Рассмотрим
произвольное разбиение ![]() отрезка
отрезка ![]() и
промежуточный набор точек
и
промежуточный набор точек ![]() , а также разбиение
, а также разбиение ![]() отрезка
отрезка ![]() , точки
которого симметричны точкам разбиения
, точки
которого симметричны точкам разбиения ![]() относительно
0, и набор промежуточных точек
относительно
0, и набор промежуточных точек ![]() на отрезках разбиения
на отрезках разбиения ![]() .
.
Очевидно,
![]() ,
, ![]() , где
, где ![]() ,
, ![]() .
.
Пусть ![]() - разбиение отрезка
- разбиение отрезка ![]() .
.
Тогда, очевидно,


={в силу нечетности ![]() } =
} =
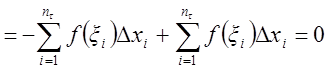 .
.
Переходя в этом
равенстве к пределу при ![]() (а, следовательно,
(а, следовательно, ![]() ), получим
), получим
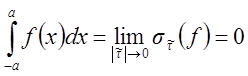 .
.
Аналогично доказывается утверждение 1).
Следствие 2: Пусть ![]() непрерывна на всей числовой оси
и периодическая с минимальным периодом
непрерывна на всей числовой оси
и периодическая с минимальным периодом![]() . Тогда
. Тогда ![]() справедливо равенство:
справедливо равенство:
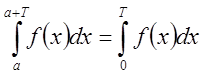 .
.
Доказательство:
Пусть
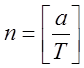 , тогда
, тогда ![]() .
.
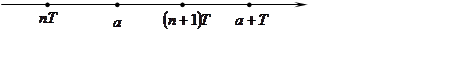
Очевидно, ![]() .
.
Тогда
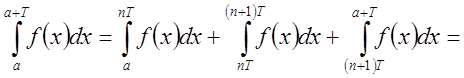
 ;
;
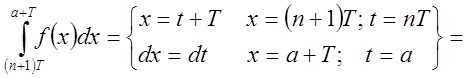
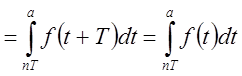 .
.Поэтому
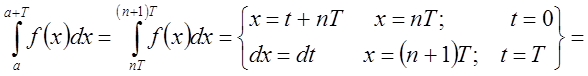
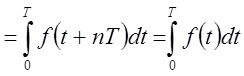 .
.
Пример
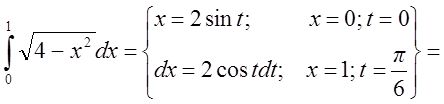
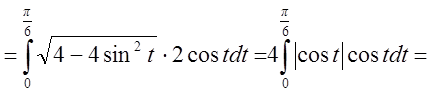
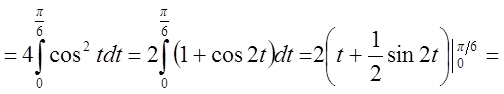
 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.