Математический анализ: Курс лекций (часть вторая "Интегральное исчисление функции одной переменной"), страница 11

Замечание 2: Если  непрерывна на   и меняет на нем знак, то  разбивается на части знакопостоянства , затем находят площади криволинейных трапеций соответствующих каждой из частей  по указанным выше правилам, и складывают. Результат сложения - это площадь всей криволинейной трапеции.

Пример

Найти площадь фигуры, ограниченной линиями ,, ,.

Решение:

            Найдем точки пересечения окружности и прямых

,

   ,   .

,

   ,   .

.

.

.

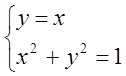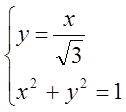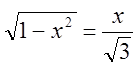
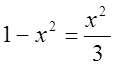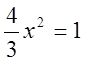
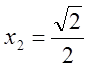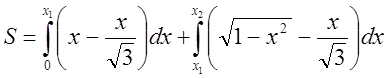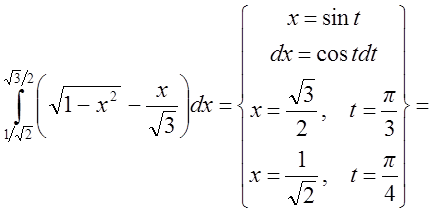
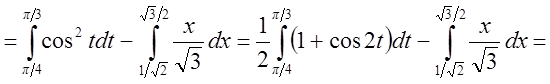
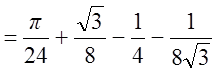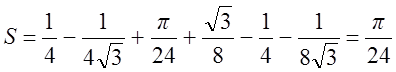 (кв. ед.)

2.15.4. Площадь криволинейного сектора

             

Пусть кривая  задана в полярной системе координат уравнением           

,  ,

 причем  непрерывна  на

  и  

.

Определение: Криволинейным сектором называют плоскую фигуру, ограниченную кривой  и лучами  и .

Теорема: Криволинейный сектор есть квадрируемая фигура, площадь которой вычисляется по формуле

.

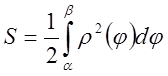Доказательство:

Пусть  произвольное разбиение отрезка .

Пусть , , . Для каждого отрезка разбиения  построим круговые секторы, радиусы которых равны  и . В результате получим две ступенчатые фигуры, первая из которых содержит круговой сектор, а вторая содержится в нем.

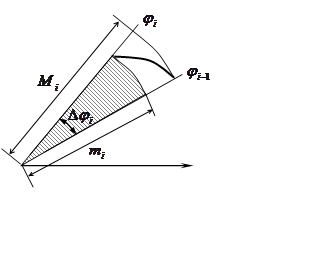
Площади этих ступенчатых фигур, очевидно, соответственно равны:

 и .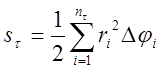

Очевидно также, что  - верхняя сумма Дарбу, а - нижняя сумма Дарбу для функции 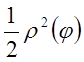  для разбиения отрезка .

Так как функция  интегрируема на , то разность  может быть сколь угодно малой. Для  (фиксированного) эта разность может быть сделана .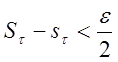

Опишем вокруг внешней ступенчатой фигуры многоугольник  и впишем во внутреннюю ступенчатую фигуру многоугольник  такие, что  и .  (Это возможно в силу квадрируемости ступенчатых фигур). Очевидно, многоугольник  описан вокруг криволинейного сектора, а  - вписан в него.

Справедливы неравенства:

                 (*)

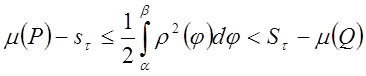(,- суммы Дарбу для интегрируемой на  функции 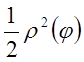 , существует  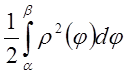и заключен между  и ).

           Следовательно, . В силу произвольности  отсюда следует, что криволинейный сектор квадрируем и из неравенства (*)  получаем, что его площадь

.

€

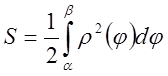Пример.

Найти площадь фигуры, ограниченной линиями ,, ,.

Решение:

              Применяя формулу площади сектора 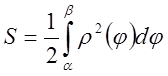 и переходя к полярным координатам, получим

  ,

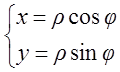
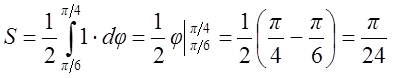(кв. ед.).

2.15.5. Вычисление объемов тел

Тело будем понимать, как часть пространства, которая ограниченна  замкнутой непересекающейся поверхностью.

Будем считать, что понятие объема многогранника известно со школы.

Введем обозначения: - многогранник,  - объем многогранника .

Свойства объемов многогранников

1⁰  (Свойство аддитивности).

Если  и  – два многогранника, не  имеющие общих точек, то объем их объединения равен сумме их объемов, то есть .

2⁰.  Если , то.

3⁰.  Если, то .

Пусть  - произвольное тело. Рассмотрим всевозможные многогранники , вписанные в это тело, и всевозможные многогранники, , описанные около .

  .

              Таким образом, объем любого из  вписанных  многогранников не превосходит объема любого из  описанных  многогранников. Это значит, что объемы вписанных многогранников имеют точную верхнюю грань, а объемы описанных – точную нижнюю грань.

 - нижний  объем тела  ;

 - верхний объем тела  .

Очевидно, .

Определение: Тело  называется кубируемым, если его верхний объем равен  его  нижнему  объему.  Их общее значение называется объемом тела . Т.е. .

Теорема 1: Тело  кубируемо тогда и только тогда, когда  существует вписанный в  многогранник  и описанный около  многогранник  такие, что .

(Доказательство аналогично доказательству о квадрируемости фигуры).

              Говорят, что объем поверхности, ограничивающей тело  равен нулю, если  существуют вписанный и описанный    многогранники, такие, что , поэтому  теорему 1 можно сформулировать:

              Тело  кубируемо, тогда и только тогда, когда ограничивающая его поверхность имеет объем, равный нулю.

Теорема 2:  Тело  кубируемо, тогда и только тогда, когда  существуют кубируемые тела

 и : .

2.15.6. Вычисление объема тела по известным площадям его поперечных сечений