Теорема: Если
основанием прямого цилиндра является квадрируемая фигура ![]() , то цилиндр есть кубируемое тело и его
объем вычисляется по формуле:
, то цилиндр есть кубируемое тело и его
объем вычисляется по формуле:
![]() ,
,
где ![]() - площадь основания
- площадь основания ![]() ,
а
,
а ![]() - высота цилиндра.
- высота цилиндра.
Доказательство:
Так как ![]() квадрируемая фигура,
то
квадрируемая фигура,
то ![]() существуют вписанная
существуют вписанная ![]() в
в ![]() и
описанная
и
описанная ![]() около
около ![]() многоугольные
фигуры, такие что:
многоугольные
фигуры, такие что: 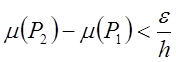 .
.
Построим призмы ![]() и
и ![]() с основаниями соответственно
с основаниями соответственно ![]() и
и ![]() и
высотой
и
высотой ![]() , тогда
, тогда
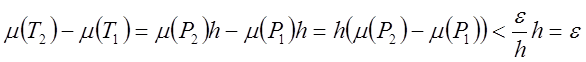
![]() .
.
Поскольку
![]() и
и ![]() являются
вписанным и описанным в цилиндр многогранниками, то цилиндр есть кубируемое
тело, и так как
являются
вписанным и описанным в цилиндр многогранниками, то цилиндр есть кубируемое
тело, и так как![]() , то
, то ![]() .
.
Рассмотрим теперь тело ![]() ,
которое содержится между плоскостями
,
которое содержится между плоскостями ![]() ,
, ![]() . Будем рассекать тело
. Будем рассекать тело ![]() плоскостями перпендикулярными оси
плоскостями перпендикулярными оси ![]() .
.
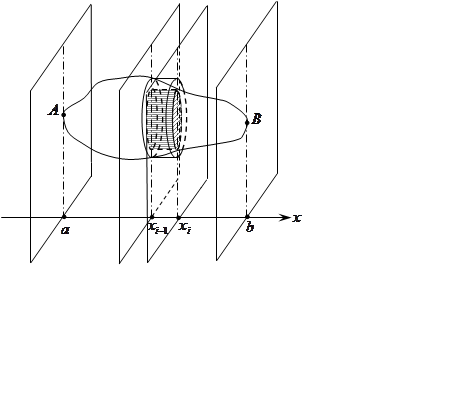
Предположим, что все эти сечения квадрируемы, и
площадь сечения, которая соответствует абсциссе ![]() (обозначим
ее через
(обозначим
ее через ![]() ), является непрерывной функцией от
), является непрерывной функцией от ![]()
![]() .
.
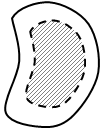 Предположим, что если два различных сечения
спроецировать на одну плоскость перпендикулярную оси
Предположим, что если два различных сечения
спроецировать на одну плоскость перпендикулярную оси ![]() ,
то их проекции содержатся одна в другой. В этом случае тело
,
то их проекции содержатся одна в другой. В этом случае тело ![]() кубируемо и его объем вычисляется по
формуле:
кубируемо и его объем вычисляется по
формуле:
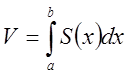 .
.
Доказательство:
Пусть ![]() произвольное
разбиение отрезка
произвольное
разбиение отрезка ![]() . Через точки разбиения проведем
плоскости, перпендикулярные оси
. Через точки разбиения проведем
плоскости, перпендикулярные оси ![]() . Эти плоскости
разобьют тело
. Эти плоскости
разобьют тело ![]() на слои. Рассмотрим
на слои. Рассмотрим ![]() - ый слой тела
- ый слой тела ![]() ,
заключенный между плоскостями
,
заключенный между плоскостями ![]() и
и ![]() .
.
Пусть
![]() ;
;
![]() .
.
Если
сечения, отвечающие различным значениям ![]() ,
спроецировать на одну из рассматриваемых плоскостей, например,
,
спроецировать на одну из рассматриваемых плоскостей, например, ![]() , то все их проекции (учитывая сделанное
выше предположение) содержатся внутри наибольшей из них, имеющей площадь
, то все их проекции (учитывая сделанное
выше предположение) содержатся внутри наибольшей из них, имеющей площадь ![]() и содержат в себе наименьшую, имеющую площадь
и содержат в себе наименьшую, имеющую площадь
![]() . Построим прямые цилиндры с образующими
параллельными оси
. Построим прямые цилиндры с образующими
параллельными оси ![]() и основаниями с наибольшей и
наименьшей проекциями. Объемы этих цилиндров будут равны:
и основаниями с наибольшей и
наименьшей проекциями. Объемы этих цилиндров будут равны: ![]() ,
, ![]() .
. ![]() - ый слой тела
- ый слой тела ![]() содержится
в большем из этих цилиндров и содержит в себе меньший. Из входящих цилиндров
составится тело
содержится
в большем из этих цилиндров и содержит в себе меньший. Из входящих цилиндров
составится тело ![]() , из выходящих – тело
, из выходящих – тело ![]() , причем
, причем
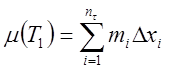 ,
,
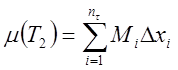 .
.
Очевидны
неравенства 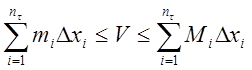 . С другой стороны, левая и
правая суммы этих неравенств являются суммами Дарбу для функции
. С другой стороны, левая и
правая суммы этих неравенств являются суммами Дарбу для функции ![]() на
на ![]() ,
следовательно, при
,
следовательно, при ![]() имеют общий предел (так как
имеют общий предел (так как ![]() - непрерывна)
- непрерывна)
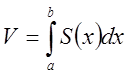 .
.
 Теорема: Пусть
функция
Теорема: Пусть
функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() .
.
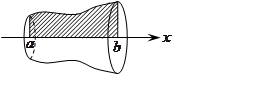
Тогда тело ![]() , образованное вращением
вокруг оси
, образованное вращением
вокруг оси ![]() криволинейной трапеции, ограниченной графиком
функции
криволинейной трапеции, ограниченной графиком
функции ![]() , прямыми
, прямыми ![]() ,
, ![]() и осью
и осью ![]() кубируемо
и его объём равен
кубируемо
и его объём равен
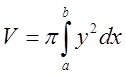 .
.
Доказательство:
Без ограничения общности можно считать, что ![]() .
.
Полученное в результате вращения криволинейной
трапеции, ограниченной кривой ![]() , тело, очевидно,
подходит под рассмотренный в предыдущем пункте случай, т.к. все его сечения
проектируются на перпендикулярную к оси
, тело, очевидно,
подходит под рассмотренный в предыдущем пункте случай, т.к. все его сечения
проектируются на перпендикулярную к оси ![]() плоскость
в виде концентрических кругов.
плоскость
в виде концентрических кругов.
Причём, очевидно,
![]() .
.
Поэтому
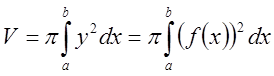 .
.
Пусто дана незамкнутая кривая ![]() .
Рассмотрим некоторую ось в пространстве и найдём площадь поверхности вращения
линии
.
Рассмотрим некоторую ось в пространстве и найдём площадь поверхности вращения
линии ![]() вокруг этой оси.
вокруг этой оси.
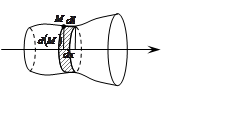 |
Возьмём на ![]() т.
т. ![]() и маленький элемент
и маленький элемент ![]() дуги кривой. Этот элемент описывает в
пространстве полоску, площадь которой приближенно равна
дуги кривой. Этот элемент описывает в
пространстве полоску, площадь которой приближенно равна
![]() ,
,
где ![]() -
расстояние точки
-
расстояние точки ![]() от оси вращения.
от оси вращения.
Вся поверхность вращения находится как интеграл
![]() .
.
Пусть
![]() и т.
и т.![]() .
.
Тогда ![]() ,
,
![]() и
и
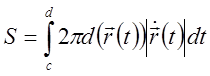 ,
, ![]() .
.
Рассмотрим случай, когда кривая ![]() есть плоская кривая, лежащая в верхней
полуплоскости плоскости
есть плоская кривая, лежащая в верхней
полуплоскости плоскости ![]() и задана уравнением
и задана уравнением ![]() . Тогда, очевидно, площадь поверхности
вращения этой кривой вокруг оси
. Тогда, очевидно, площадь поверхности
вращения этой кривой вокруг оси ![]() будет
будет
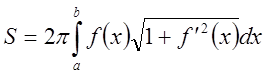 .
.
Определение: Пусть дана материальная точка массы ![]() . Ее
статическим моментом относительно прямой
. Ее
статическим моментом относительно прямой ![]() называют
произведение массы этой точки на расстояние
называют
произведение массы этой точки на расстояние ![]() до
прямой
до
прямой ![]() .
.
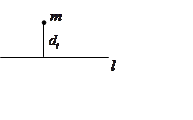
![]()
Определение: Статическим моментом точки относительно плоскости называется произведение массы точки на расстояние от данной точки до данной плоскости.
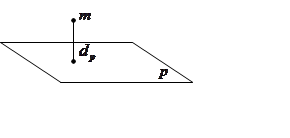
![]()
Определение: Моментом инерции точки относительно прямой ![]() называется
произведение массы точки на квадрат её расстояния до прямой
называется
произведение массы точки на квадрат её расстояния до прямой![]() .
.
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.