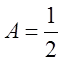 ,
, 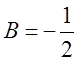 ,
, 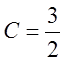 ,
, ![]() ,
,
![]() ,
, 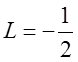 ,
, 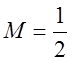 .
.
Поэтому
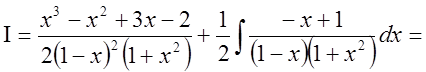
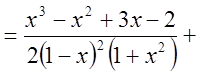
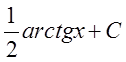 .
.
2. Применим метод Остроградского для вычисления интеграла
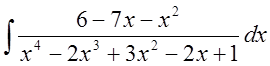 .
.
Решение:
![]()
![]()
![]()
![]()
![]()
Тогда, так как ![]() , то
, то
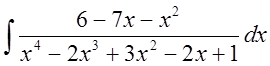
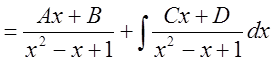 .
.
Далее решение аналогично решению примера 1.
![]() - рациональная функция
переменных (от функций)
- рациональная функция
переменных (от функций) ![]() ,
, ![]() .
.
Интегралы
вида ![]() находятся с помощью (универсальной)
подстановки
находятся с помощью (универсальной)
подстановки 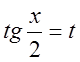
![]() .
.
Посредством
этой подстановки ![]() преобразуется к интегралу от
рациональной функции.
преобразуется к интегралу от
рациональной функции.
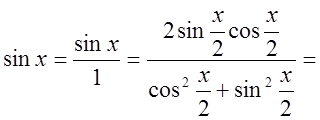
![]() {разделим числитель и знаменатель на
{разделим числитель и знаменатель на 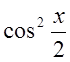 }
}![]()
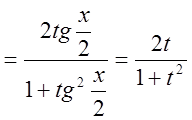 .
.
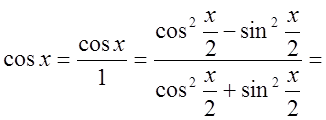
![]() {разделим числитель и знаменатель на
{разделим числитель и знаменатель на 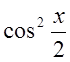 }
}![]()
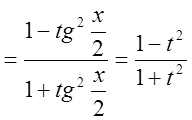 .
.
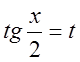 ,
, 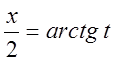 ,
, ![]()
![]()
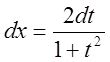 .
.
Тогда
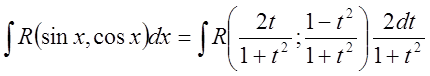 .
.
Пример.
Найти интеграл 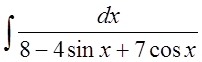 .
.
Решение:
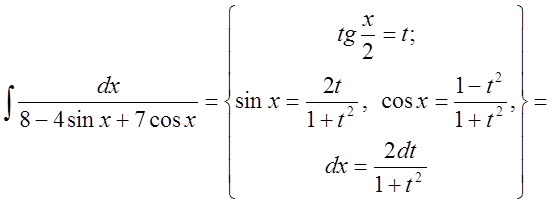
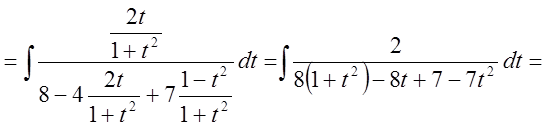
 .
.
Разложим подынтегральную функцию (рациональную дробь) на простейшие дроби.
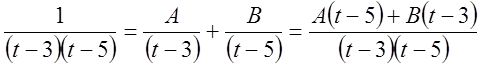 .
.
![]()
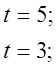
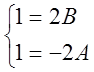
![]()
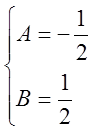 ,
,
тогда
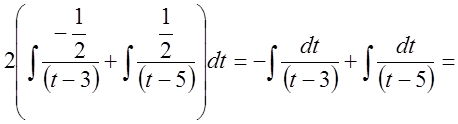
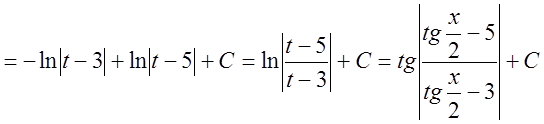 .
.
Универсальная подстановка часто приводит к громоздким выкладкам, поэтому иногда лучше применять другие подстановки.
Из
алгебра известно, что если ![]() , то функцию
, то функцию ![]() можно представить в виде
можно представить в виде
![]() ,
,
если ![]() ,
то
,
то ![]() .
.
Поэтому:
1) если ![]() , то
, то
![]()
![]() ,
,
и рационализация достигается
подстановкой ![]() .
.
2) если![]() ,
,
то
![]()
![]()
и рационализация достигается
подстановкой ![]() .
.
3) если ![]() , то
, то
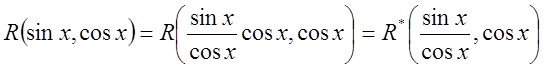 ,
,
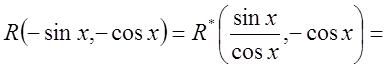
![]() {в силу свойства этой функции}
{в силу свойства этой функции}![]()
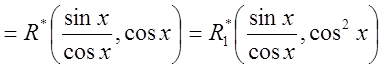 .
.
Тогда
![]()
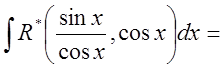
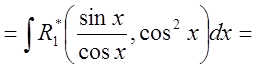
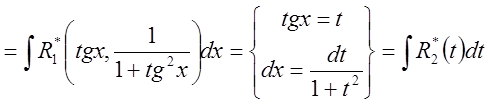 .
.
Замечание: Имеют место равенства
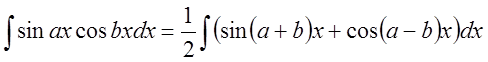 ,
,
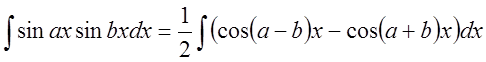 ,
,
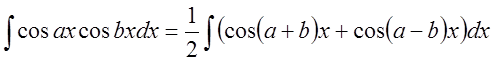 .
.
Тригонометрические подстановки
1.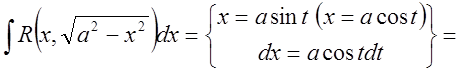
![]()
![]()
![]() .
.
2. 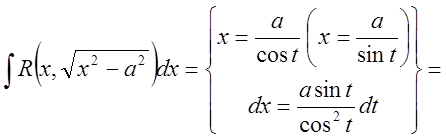
![]()
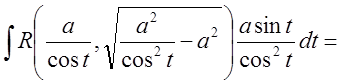
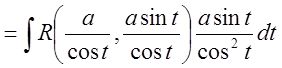 .
.
3. 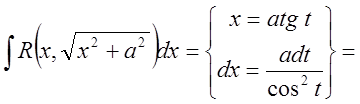
![]()
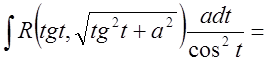
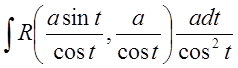 .
.
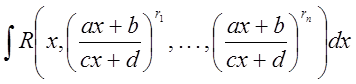
Будем считать, что ![]() -
рациональные числа,
-
рациональные числа, ![]() - действительные и
- действительные и 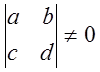 , (поскольку в противном случае выражение
, (поскольку в противном случае выражение 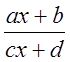 не зависит от
не зависит от ![]() и под интегралом
будет рациональная функция от
и под интегралом
будет рациональная функция от ![]() ).
).
Пусть ![]() - общий знаменатель чисел
- общий знаменатель чисел ![]() , т.е.
, т.е. 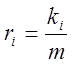 ,
,
(![]() - целое
- целое
![]() ).
).
Положим
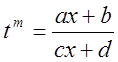
![]()
![]()
![]()
![]()
![]()
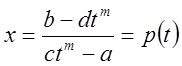 - рациональная
функция,
- рациональная
функция,
![]() , где
, где ![]() - рациональная функция.
- рациональная функция.
Тогда
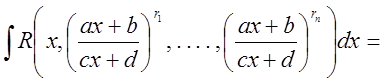
![]() ,
,
где![]() - рациональная функция.
- рациональная функция.
Примеры:
1.
Найти интеграл 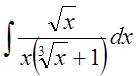 .
.
Решение:
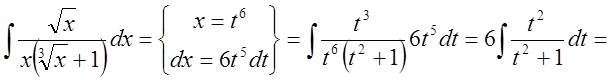
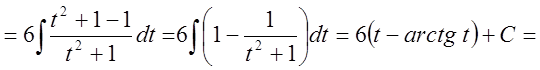
![]() .
.
2.
Найти интеграл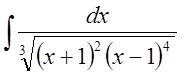 .
.
Решение:
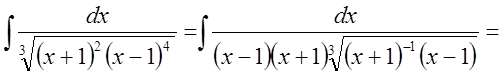
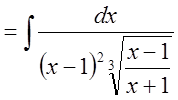
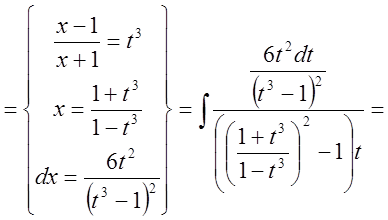
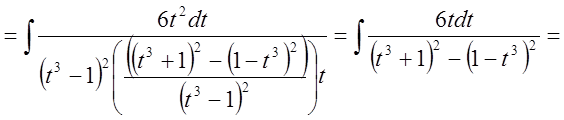
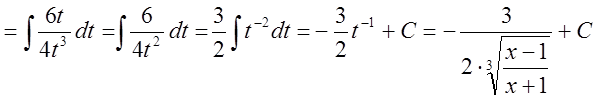 .
.
Подстановки Эйлера
1. Пусть ![]() и
и ![]() . Тогда полагают
. Тогда полагают
![]() - знаки можно выбрать произвольно.
- знаки можно выбрать произвольно.
![]()
![]()
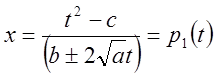 - рациональная
функция.
- рациональная
функция.
Тогда и![]() рациональная функция.
рациональная функция.
![]() ,
,
![]() - рациональная
функция.
- рациональная
функция.
Таким образом,
![]() ,
,
где ![]() -
рациональная функция.
-
рациональная функция.
2.
Пусть ![]() и
и ![]() . Тогда
полагают
. Тогда
полагают
![]() - знаки
можно выбрать произвольно.
- знаки
можно выбрать произвольно.
![]() ;
;
![]() ;
;
![]() ;
;
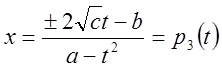 - рациональная
функция.
- рациональная
функция.
Тогда и ![]() рациональная.
рациональная.
![]() ,
,
![]() - рациональная функция.
- рациональная функция.
Таким образом,
![]() ,
,
где ![]() -
рациональная функция.
-
рациональная функция.
3. Пусть
![]() и
и ![]() ,
, ![]() - действительные корни.
- действительные корни.
1) ![]()
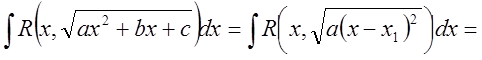
![]() - интеграл от
рациональной функции.
- интеграл от
рациональной функции.
2) ![]()
Положим, ![]() или
или
![]()
![]()
![]()
![]()
![]()
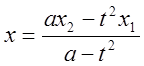
![]() -
рациональная функция.
-
рациональная функция.
Тогда и![]() рациональная.
рациональная.
![]() ,
,
![]() - рациональная функция.
- рациональная функция.
Таким образом,
![]() ,
,
где ![]() -
рациональная функция.
-
рациональная функция.
Замечание 1.
Если ![]() ,
, ![]() , то
, то
![]()
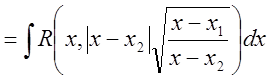 .
.
Последний из интегралов принадлежит к виду, интегрирование которых рассмотрено ранее.
Замечание 2.
Даже в случае если![]() ,
,![]() и
и
![]() , то можно применять подстановку 1 или подстановку
2.
, то можно применять подстановку 1 или подстановку
2.
Пример
Найти интеграл 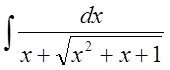
Решение:
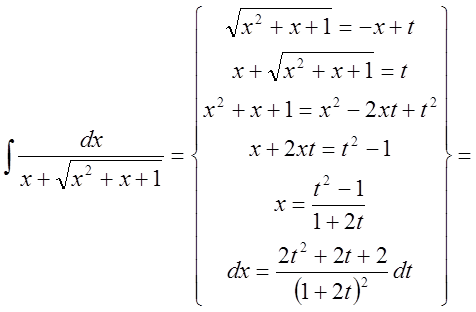
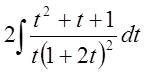
Разложим подинтегральную функцию на простейшие дроби.
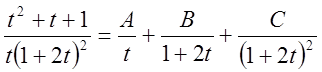
![]()
![]()
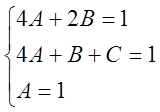
![]()
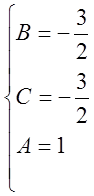
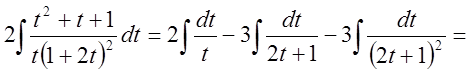
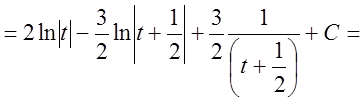
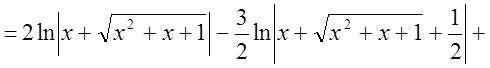
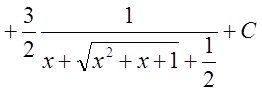 .
.
Определение:
Выражение вида ![]() называется дифференциальным биномом, где
называется дифференциальным биномом, где ![]() ,
, ![]() ,
, ![]() ,
, ![]() -
рациональные.
-
рациональные.
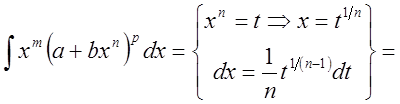
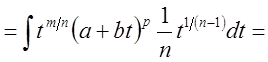
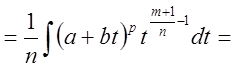 {
{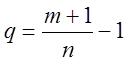 }
}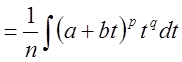 .
.
Рассмотрим случаи:
1.
![]() - целое,
- целое,
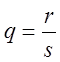 ,
, ![]() - целые.
- целые.
Замена: ![]()
![]()
![]() ,
, ![]() .
.
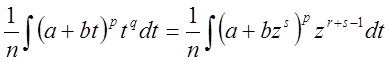 .
.
Получили интеграл от рациональной функции.
2.
![]() - целое,
- целое,
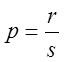 ,
, ![]() - целые.
- целые.
Замена: ![]()
![]()
![]() ,
, 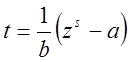 ,
, 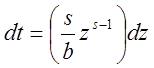 .
.
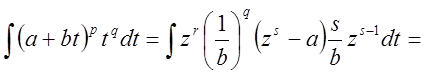
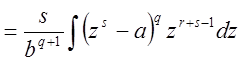 .
.
Получили интеграл от рациональной функции.
3.
![]() - целое,
- целое,
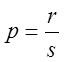 ,
, ![]() - целые.
- целые.
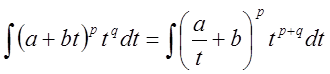 .
.
Тогда
подстановка 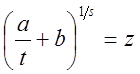 приводит этот интеграл к
интегралу от рациональной функции.
приводит этот интеграл к
интегралу от рациональной функции.
Применительно
к интегралу ![]() мы рассмотрели случаи:
мы рассмотрели случаи:
|
1) |
2) |
3) |
Им соответствуют подстановки (подстановки Чебышева):
1) 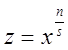 , где
, где ![]() -
знаменатель дроби
-
знаменатель дроби 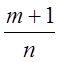 ;
;
2) 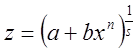 , где
, где ![]() -
знаменатель дроби
-
знаменатель дроби 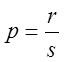 ;
;
3)
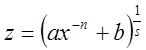 , где
, где ![]() -
знаменатель дроби
-
знаменатель дроби 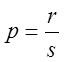 .
.
Чебышев
показал, что если и ![]() , и
, и 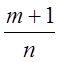 , ни
, ни 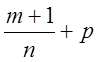 - не являются целыми числами, то интеграл
от дифференциального бинома не может быть выражен в конечном виде в элементарных
функциях.
- не являются целыми числами, то интеграл
от дифференциального бинома не может быть выражен в конечном виде в элементарных
функциях.
Пример
Найти интеграл 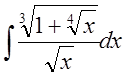 .
.
Решение:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.