Пусть задана кривая ![]() и
непересекающая ее прямая
и
непересекающая ее прямая ![]() . Будем считать, что на
кривой распределена масса с плотностью
. Будем считать, что на
кривой распределена масса с плотностью ![]() (задана
линейная плотность кривой)
(задана
линейная плотность кривой)
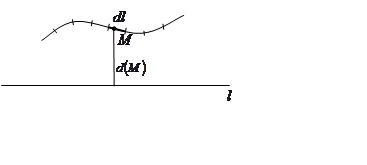
Под линейной плотностью кривой понимаем предел
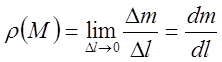 ,
,
где![]() – длина дуги, которой принадлежит т.
– длина дуги, которой принадлежит т. ![]() ;
;
![]() – масса дуги
– масса дуги ![]() . (при
. (при ![]() дуга стягивается в точку
дуга стягивается в точку ![]() ).
).
Найдём статический момент кривой относительно прямой.
Пусть ![]() – произвольная точка
кривой. Рассмотрим элементарную дугу длины
– произвольная точка
кривой. Рассмотрим элементарную дугу длины ![]() ,
содержащую точку
,
содержащую точку ![]() . Пусть масса этой дуги
. Пусть масса этой дуги ![]() и расстояние от точки
и расстояние от точки ![]() до прямой
до прямой ![]() равно
равно ![]() .
.
Тогда
![]()
и
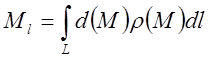 .
.
Зададим кривую ![]() радиус
- вектором
радиус
- вектором ![]() .
.
Тогда
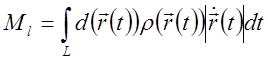 .
.
Частные случаи:
1.
Предположим, что кривая лежит на плоскости ![]() и задана в параметрической форме
и задана в параметрической форме ![]() ,
, ![]() ,
, ![]() .
.
Тогда, очевидно,
 ;
;
 .
.
2. Если кривая
задана на плоскости ![]() в явном виде
в явном виде ![]() ,
, ![]() ,
, ![]() , то
, то
 ;
;
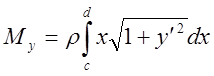 .
.
Определение: Центром масс системы материальных точек называется точка с
координатами ![]() , такая, что если в ней
сосредоточить всю массу системы, то статические моменты данной материальной
точки относительно любой координатной плоскости равны соответствующим моментам
системы.
, такая, что если в ней
сосредоточить всю массу системы, то статические моменты данной материальной
точки относительно любой координатной плоскости равны соответствующим моментам
системы.
![]()
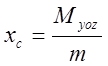
![]()
![]()
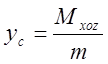
![]()
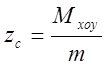
В развернутом виде
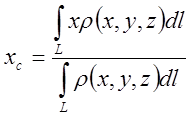 ;
; 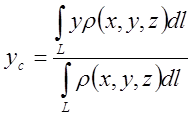 ;
; 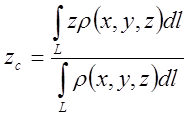 .
.
Теорема: Площадь поверхности, полученной в результате вращения кривой вокруг непересекающей ее оси, равна произведению длины кривой на длину окружности, описанной центром тяжести кривой.
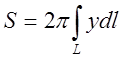
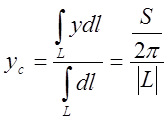
Следовательно,
![]() .
.
Пример.
Найти координаты центра тяжести полуокружности радиуса ![]() .
.
Решение:
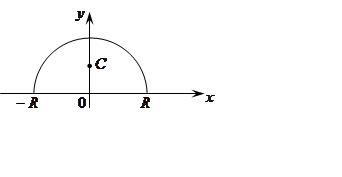
Очевидно
![]() .
.
Чтобы
найти ![]() , воспользуемся теоремой Гульдина:
, воспользуемся теоремой Гульдина:
![]() .
.
![]() ,
, ![]()
![]()
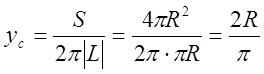 .
.
Координаты центра тяжести
полуокружности 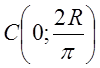 .
.
Пусть дана фигура, ограниченная линиями ![]() ,
, ![]() ,
, ![]() ,
,![]() . В этой фигуре распределена
масса с поверхностной плотностью
. В этой фигуре распределена
масса с поверхностной плотностью
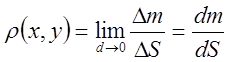 ,
, ![]() .
.
где
![]() – часть (малая) фигуры, содержащая точку
– часть (малая) фигуры, содержащая точку ![]() ;
;
![]() – максимальный диаметр площадки
– максимальный диаметр площадки ![]() ;
;
![]() – масса
– масса ![]() (при
(при ![]() площадка
площадка ![]() стягивается
в точку
стягивается
в точку ![]() ).
).
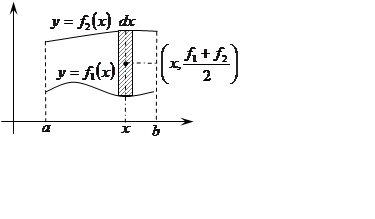
Найдём статические моменты плоской фигуры относительно
осей ![]() и
и ![]() . Пусть
. Пусть
![]() . Разобьем фигуру на элементарные полоски
и выделим элементарную полоску шириной
. Разобьем фигуру на элементарные полоски
и выделим элементарную полоску шириной ![]() на расстоянии
на расстоянии
![]() (см. рис.). Очевидно, центр масс этой
полоски находится в точке
(см. рис.). Очевидно, центр масс этой
полоски находится в точке 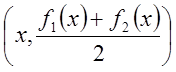 – пересечения диагоналей.
– пересечения диагоналей.
Тогда
![]()
и
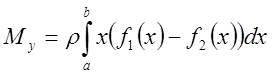 .
.
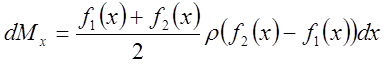
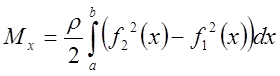 .
.
Масса рассматриваемой фигуры, очевидно, равна
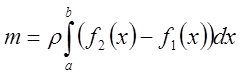 .
.
Если
![]() - центр масс фигуры, то
- центр масс фигуры, то ![]() ,
, ![]()
![]()
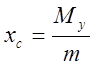 ,
, 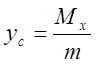 .
.
Замечание: Объём
тела, полученного в результате вращения фигуры вокруг оси ![]() , равен
, равен
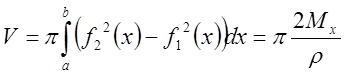 .
.
Тогда
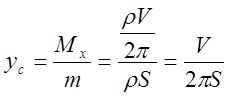
![]()
![]() .
.
Теорема: Объём тела вращения фигуры вокруг непересекающей ее оси равен площади этой фигуры, умноженной на длину окружности, описываемой центром масс фигуры.
Пример
Найти координаты центра тяжести полукруга радиуса ![]() .
.
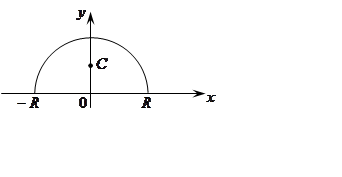
Очевидно,
![]() .
.
По второй теореме Гульдина
![]() .
.
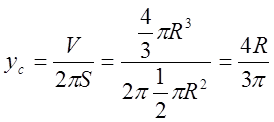 .
.
Координаты
центра тяжести круга 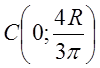 .
.
Работа
Пример.
Какую работу необходимо затратить, чтобы выкачать жидкость из резервуара,
имеющего форму параллелепипеда со сторонами ![]() .
.
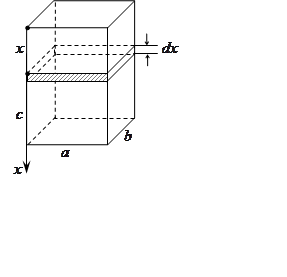 Пусть
Пусть ![]() . На глубине
. На глубине ![]() рассмотрим
элементарный слой жидкости толщиной
рассмотрим
элементарный слой жидкости толщиной ![]() .
.
Масса
этого слоя ![]() ,
,
а вес
![]() .
.
Элементарная работа по выкачиванию этого слоя будет равна
![]() .
.
Вся
работа 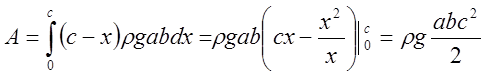 .
.
Определение:Пусть функция ![]() определена
на
определена
на ![]() ,
, ![]() и
интегрируема по Риману на отрезке
и
интегрируема по Риману на отрезке ![]()
![]() . Если существует предел
. Если существует предел 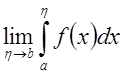 , то говорят, что функция
, то говорят, что функция ![]() интегрируема в несобственном смысле на
интегрируема в несобственном смысле на ![]() , а указанный предел называется ее
несобственным интегралом и обозначается
, а указанный предел называется ее
несобственным интегралом и обозначается 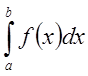 .
.
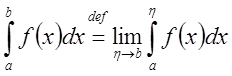 .
.
Если предел существует и конечен, то интеграл 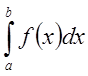 - называется сходящимся, в
противном случае - расходящимся.
- называется сходящимся, в
противном случае - расходящимся.
При ![]() говорят о
несобственном интеграле 1 рода, при
говорят о
несобственном интеграле 1 рода, при ![]() конечном – о
несобственном интеграле 2 рода.
конечном – о
несобственном интеграле 2 рода.
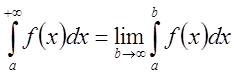 - 1 рода,
- 1 рода,
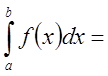 {
{![]() - неограниченна}
- неограниченна}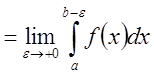 - 2 рода.
- 2 рода.
Аналогично определяются и записываются интегралы с бесконечным нижним пределом и с конечным нижним пределом, но неограниченной в нем функции:
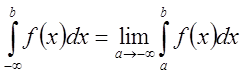 ,
,
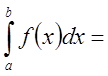 {
{![]() в точке
в точке ![]() - неограниченна}
- неограниченна}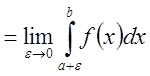 ,
,
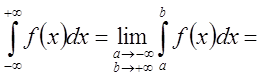
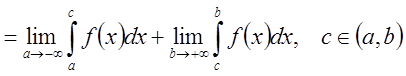 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.