Математический анализ: Курс лекций (часть вторая "Интегральное исчисление функции одной переменной"), страница 10

.

              Доказательство:

              Для доказательства применим формулы перехода от полярных координат к декартовым:

и воспользуемся общей формулой для длины дуги

 

.

€

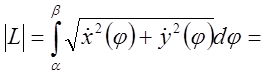
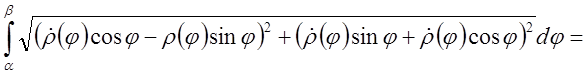
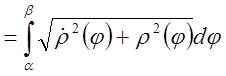Длина графика непрерывно  дифференцируемой функции

Пусть  непрерывно дифференцируемая на  функция, тогда кривая (график ) спрямляема и ее длина вычисляется по формуле:

.

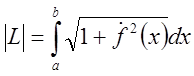              Заметим, что  есть кривая, определяемая параметрическими уравнениями, .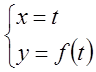

Доказательство становится очевидным.

2.15.2. Вычисление площадей плоских фигур

Определение: Многоугольной фигурой (областью) будем называть фигуру, состоящую из конечного числа многоугольников, которые не имеют общих внутренних точек.

Будем считать, что понятие площади многоугольника известно со школы.

Площадь отрезка считаем равной нулю.

Введем обозначения: - многоугольная фигура,  - площадь фигуры.

Основные свойства площадей многоугольных фигур

1⁰.  (Свойство аддитивности).

Если  и  – две многоугольные фигуры, не имеющие общих внутренних точек, то площадь их объединения равна сумме их площадей, то есть .

2⁰.  Если , то.

3⁰.  Если, то .

              Пусть  - произвольная плоская фигура. Рассмотрим всевозможные многоугольные фигуры , вписанные в , и всевозможные  многоугольные фигуры описанные вокруг нее. Вписанные содержатся внутри , описанные содержат.

 

.

              Таким образом, площадь любой вписанной многоугольной фигуры не превосходит площади любой описанной  многоугольной фигуры. Следовательно, все вписанные многоугольные фигуры имеют точную верхнюю грань, а описанные - точную нижнюю грань.

 - нижняя площадь фигуры ;

 - верхняя площадь фигуры .

Очевидно, .

Определение: Фигура  называется квадрируемой, если ее верхняя  площадь равна ее нижней площади.  Их  общее значение называется площадью фигуры . Т.е. .

Теорема 1: Фигура  квадрируема  тогда и только тогда, когда  существует вписанная в  многоугольная фигура  и описанная около многоугольная фигура  такие, что .

Доказательство:

Необходимость

Пусть  – квадрируемая фигура, т.е. . Из определения нижней и верхней площади фигуры имеем:

 ;

 .

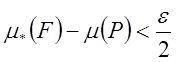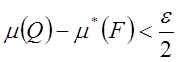Складывая неравенства, получим . Поскольку , то .

Достаточность

Пусть ,  и : , покажем, что  – квадрируемая фигура.

Из очевидного неравенства  имеем . Так как  - произвольное, то это возможно, когда , т.е.  – квадрируемая фигура.

€

              Говорят что, граница плоской фигуры  имеет площадь равную нулю, если  существует вписанная в  многоугольная фигура  и описанная около  многоугольная фигура , такие, что .  Поэтому доказанную теорему  1 можно сформулировать следующим образом:

              Фигура - квадрируема, тогда и только тогда, когда ее граница имеет площадь равную нулю.

Теорема 2:Для того чтобы  была квадрируемой, необходимо и достаточно, чтобы  существовали квадрируемые  и  :

.

2.15.3. Площадь криволинейной трапеции

Пусть  непрерывна и неотрицательна  на .

Определение: Криволинейной трапецией называется фигура, ограниченная графиком функции  и прямыми , , .

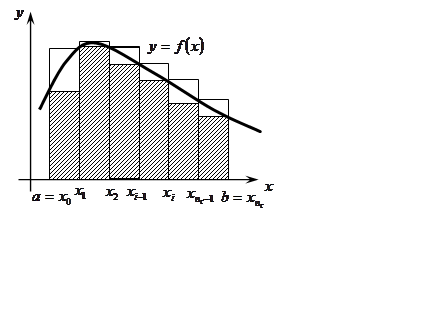Теорема:  Криволинейная трапеция есть квадрируемая фигура,  и ее площадь вычисляется по формуле:

.

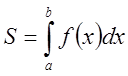Доказательство:

Так как  - непрерывна на , то .

Это означает, что  отрезка .

Очевидно, суммы  и численно равны площадям ступенчатых фигур, соответственно описанных и вписанных в криволинейную трапецию. При этом  численно равна сумме площадей прямоугольников с основаниями   и высотами , а  численно равна сумме площадей прямоугольников с теми же основаниями  и высотами .

Так как , то по теореме 1 криволинейная трапеция квадрируемая фигура, следовательно

.

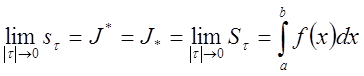Поскольку площадь криволинейной трапеции удовлетворяет неравенствам: , по теореме о двух милиционерах получаем:

.

€

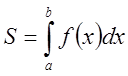Замечание 1:  Если  непрерывна на   и  , то  .