Доказательство:
Достаточно
доказать для разбиения ![]() , которое отличается от
разбиения
, которое отличается от
разбиения ![]() на одну точку
на одну точку ![]() . Пусть
. Пусть ![]() попадает внутрь отрезка
попадает внутрь отрезка ![]() . Составим верхние суммы Дарбу для
разбиений
. Составим верхние суммы Дарбу для
разбиений ![]() и
и ![]() .
.
 ,
,
где
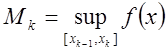 ;
;
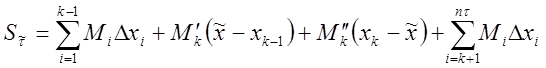 ,
,
где 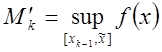 ,
,
 .
.
Очевидно, ![]() и
и ![]() ,
поэтому
,
поэтому
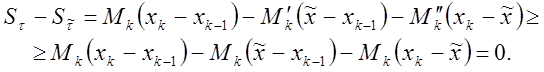
Откуда следует, что ![]() .
.
Аналогично
доказывается, что ![]() .
.
20.
Любая нижняя сумма не превосходит любой верхней суммы, даже и отвечающей
другому разбиению отрезка ![]() .
.
Доказательство:
Рассмотрим
два различных разбиения ![]() и
и ![]() отрезка
отрезка ![]() и
докажем, что
и
докажем, что ![]() .
.
Объединив точки разбиений ![]() и
и ![]() ,
получим
,
получим ![]() . По свойству 1 следует, что
. По свойству 1 следует, что ![]() и
и ![]() , из
свойства 1
, из
свойства 1![]() . Тогда
. Тогда ![]()
![]()
![]() .
.
Из
доказанного следует, что множество ![]() нижних сумм ограничено
сверху, например, любой верхней суммой
нижних сумм ограничено
сверху, например, любой верхней суммой ![]() и,
следовательно, имеет точную верхнюю грань
и,
следовательно, имеет точную верхнюю грань ![]() .
.
Множество
верхних сумм ![]() ограничено снизу, например числом
ограничено снизу, например числом ![]() , поэтому существует его точная нижняя
грань
, поэтому существует его точная нижняя
грань ![]() , причем, очевидно
, причем, очевидно ![]() .
.
Таким образом, ![]() для любых нижней и верхней суммы Дарбу.
для любых нижней и верхней суммы Дарбу.
Числа ![]() и
и ![]() называются
соответственно верхним и нижним интегралами Дарбу от функции
называются
соответственно верхним и нижним интегралами Дарбу от функции ![]() .
.
30.
Если функция ![]() ограничена на
ограничена на ![]() , то имеют место следующие равенства:
, то имеют место следующие равенства:
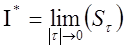 и
и ![]() .
.
Доказательство:
Заметим, что 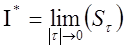 означает, что
означает, что
![]()
![]() отрезка
отрезка
![]()
Рассмотрим два разбиения ![]() и
и ![]() отрезка
отрезка ![]() ,
, ![]() , причем
, причем
![]() отличается от
отличается от ![]() на одну точку
на одну точку ![]() , т.е.
, т.е. ![]() ,
, ![]() . Из доказательства свойства 2 имеем
. Из доказательства свойства 2 имеем
![]() .
.
Очевидно,
![]() ,
, ![]() , где
, где ![]()
и ![]() , где
, где ![]() .
.
Тогда
![]()
![]() .
.
Итак, ![]() .
.
Пусть теперь![]() отличается от
отличается от ![]() на
на ![]() точек
точек ![]() :
:
![]() ,
, ![]() , . . . ,
, . . . , ![]() .
.
Очевидно,
![]()
![]()
…………………………..
![]() .
.
Сложив левые и правые части неравенств, получим
![]() .
.
Из
того, что ![]()
![]()
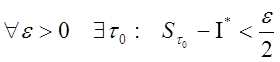 .
Выберем
.
Выберем  , где
, где ![]() - число
точек разбиения.
- число
точек разбиения.
Пусть ![]() произвольное разбиение
произвольное разбиение![]() , такое, что
, такое, что ![]() .
Рассмотрим разбиение
.
Рассмотрим разбиение ![]() . Тогда
. Тогда
 .
.
Итак, имеем 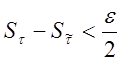 .
.
С другой стороны, разбиение ![]() можно
рассматривать как разбиение, полученное
из
можно
рассматривать как разбиение, полученное
из![]() добавлением к нему точек разбиения
добавлением к нему точек разбиения ![]() , поэтому по свойству 1
, поэтому по свойству 1
![]()
![]()
![]() .
.
Тогда
в соответствии с неравенством 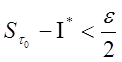 получаем
получаем 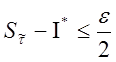 .
.
Складывая
неравенства 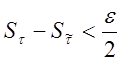 и
и 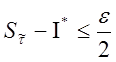 ,
получим
,
получим
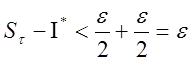
![]()
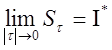 .
.
Аналогично доказывается и
равенство ![]() .
.
Теорема: Следующие утверждения эквивалентны:
1. Функция ![]() интегрируема по Риману
на
интегрируема по Риману
на ![]() ;
;
2. ![]() ;
;
3. ![]() (критерий Дарбу);
(критерий Дарбу);
4. ![]() (критерий Римана).
(критерий Римана).
Доказательство:
1. Докажем, что из первого утверждения следует второе:
Пусть
![]() интегрируема на
интегрируема на ![]() ,
т.е. существует
,
т.е. существует 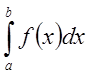 .
.
Это
означает, ![]()
![]() разбиения
разбиения ![]() отрезка
отрезка  .
.
Из последнего неравенства
имеем  .
.
Ранее мы установили, что числа ![]() и
и
![]() являются соответственно точной верхней и
точной нижней гранями интегральных сумм, на множестве всех промежуточных точек
разбиения
являются соответственно точной верхней и
точной нижней гранями интегральных сумм, на множестве всех промежуточных точек
разбиения ![]() , следовательно,
, следовательно,
 .
.
Тогда ![]() ,
следовательно,
,
следовательно, ![]() .
.
2. Докажем, что из второго утверждения следует четвертое:
Пусть ![]() ,
что означает:
,
что означает: ![]()
![]() разбиения
разбиения ![]() отрезка
отрезка
![]() .
.
Пусть ![]() такое,
что
такое,
что ![]() . Тогда
. Тогда ![]() .
.
3. Докажем, что из четвертого утверждения следует третье:
Пусть
![]() .
.
Очевидно, ![]()
![]()
![]()
![]()
![]() в силу произвольности
в силу произвольности ![]() .
.
4. Докажем, что из третьего утверждения следует первое:
Пусть
![]() . Обозначим
. Обозначим ![]() .
Известно, что
.
Известно, что ![]() . Переходя к пределу при
. Переходя к пределу при ![]() , получим,
, получим, ![]() (
(![]() ,
,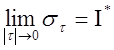 ).
).
Это означает, что ![]() -
интегрируема на
-
интегрируема на ![]() .
.
Пример 1: Пусть
![]()
![]() на
на ![]() . Показать, что
. Показать, что![]() интегрируема
на
интегрируема
на ![]() , и найти интеграл от нее.
, и найти интеграл от нее.
Решение:
Возьмем
произвольное разбиение ![]() .
.
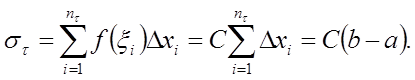
Следовательно, ![]() , т.е.
, т.е. 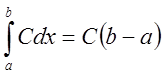 .
.
Пример 2: Интегрируема ли функция Дирихле.
 на
на ![]() .
.
Решение:
Найдем
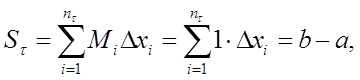
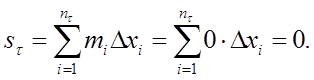
Тогда
![]() , следовательно, данная функция не
интегрируемая по Риману на любом отрезке.
, следовательно, данная функция не
интегрируемая по Риману на любом отрезке.
Пусть функция ![]() определена на отрезке
определена на отрезке ![]() и пусть
и пусть
![]()
![]() .
.
Определение: Число ![]() называется
колебанием функции
называется
колебанием функции ![]() на
отрезке
на
отрезке ![]() .
.
Очевидно,
![]() ,
,
![]() .
.
Рассмотрим ![]() - некоторое разбиение
отрезка
- некоторое разбиение
отрезка ![]() . Пусть
. Пусть
![]() ,
,
![]() ,
,
тогда ![]() -
колебание функции
-
колебание функции ![]() на
на ![]() .
.
Запишем разность:
 .
.
Итак, для любого разбиения ![]() отрезка
отрезка
![]() справедливо равенство:
справедливо равенство:
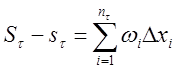 .
.
Поэтому можно сформулировать следующий критерий интегрируемости функции на отрезке.
Теорема: Ограниченная на отрезке ![]() функция
функция
![]() интегрируема (по Риману) на нем тогда и только тогда,
когда
интегрируема (по Риману) на нем тогда и только тогда,
когда 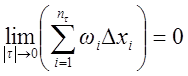 или
или
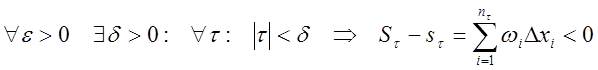 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.