Перепишем
интеграл в виде 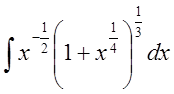 .
.
В данном примере  ,
,  ,
,  .
.
Составим
выражение 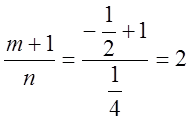 - целое число. Следовательно, здесь мы
имеем второй случай интегрируемости.
- целое число. Следовательно, здесь мы
имеем второй случай интегрируемости.
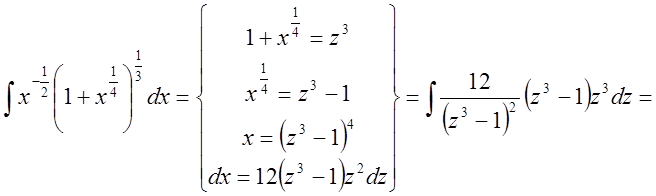
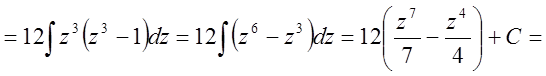
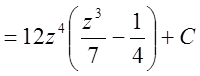
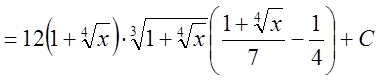 .
.
Замечание. Как видим, не все интегралы от элементарных функций выражаются в конечном виде в элементарных функциях. К числу таких интегралов (кроме уже рассмотренных) в частности относятся
![]() ,
, ![]() ,
, ![]() ,
,  ,
,  ,
, 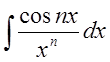 ,
, 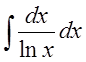 .
.
Пусть
дан отрезок ![]() .
.
Определение: Разбиением ![]() отрезка
отрезка ![]() называется
любое множество его точек
называется
любое множество его точек ![]() ,
, ![]() , включающие концы отрезка и такое, что
, включающие концы отрезка и такое, что
![]()
при этом пишут ![]() .
.
Каждый из отрезков ![]() ,
, ![]() называется отрезком разбиения,
а
называется отрезком разбиения,
а ![]()
![]() его длиной
его длиной ![]() . Величину
. Величину ![]() называют
диаметром разбиения.
называют
диаметром разбиения.
Определение: Назовём ![]() измельчением (продолжением) разбиения
измельчением (продолжением) разбиения ![]() , если всякая точка разбиения
, если всякая точка разбиения ![]() является точкой разбиения
является точкой разбиения ![]() . Очевидно,
. Очевидно, ![]() .
.
Пусть
![]() .
.
Тогда из того, что
![]()
![]()
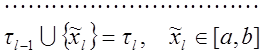 ,
,
получим
![]() .
.
Пусть на отрезке ![]() определена
ограниченная функция
определена
ограниченная функция ![]() и
и ![]() -
некоторое разбиение
-
некоторое разбиение ![]() . Выберем в каждом отрезке
. Выберем в каждом отрезке ![]() произвольную точку
произвольную точку ![]() и
составим сумму
и
составим сумму![]()
 .
.
Эта
сумма называется интегральной суммой Римана для функции ![]() ,
соответствующая разбиению
,
соответствующая разбиению ![]() и данному набору
(выбору) точек
и данному набору
(выбору) точек ![]() , т.е. набору
, т.е. набору ![]() .
.
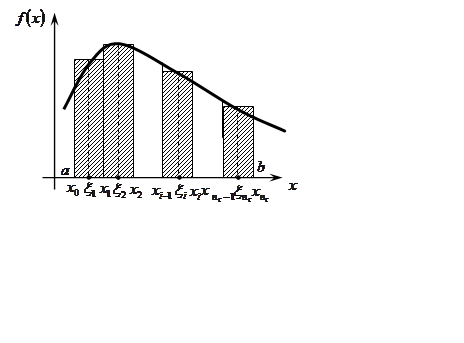
Геометрически
(если ![]() ) интегральная сумма – сумма площадей
прямоугольников, основаниями которых являются отрезки
) интегральная сумма – сумма площадей
прямоугольников, основаниями которых являются отрезки ![]() ,
а высоты равны
,
а высоты равны ![]() .
.
Пусть![]() ,
,
![]() .
.
Тогда ![]()
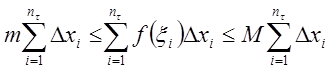 ,
,
![]() .
.
Рассмотрим
последовательность разбиений ![]() отрезка
отрезка ![]() -
- ![]() , таких
что
, таких
что ![]() , и соответствующие последовательности
интегральных сумм
, и соответствующие последовательности
интегральных сумм ![]() .
.
Определение: Число ![]() называется пределом интегральных сумм
называется пределом интегральных сумм ![]() при
при ![]() если:
если:
![]() ,
,
при любом выборе точек ![]() на каждом из отрезков
на каждом из отрезков ![]() разбиения.
разбиения.
Определение: Функция ![]() называется интегрируемой по Риману на
называется интегрируемой по Риману на ![]() , если существует конечный предел
, если существует конечный предел![]() интегральных сумм этой функции при
интегральных сумм этой функции при ![]() , этот предел называется интегралом Римана
или определенным интегралом от
, этот предел называется интегралом Римана
или определенным интегралом от ![]() на
на ![]() и обозначается
и обозначается
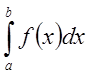 .
.
По определению полагают:
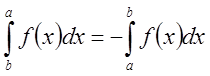 ,
, 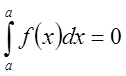 .
.
Теорема: Если ![]() интегрируема по Риману на
интегрируема по Риману на ![]() , то она на нем ограничена.
, то она на нем ограничена.
Доказательство:
Заметим, что если ![]() интегрируема на
интегрируема на ![]() ,
то все ее интегральные суммы с достаточно малым диаметром разбиения ограничены.
,
то все ее интегральные суммы с достаточно малым диаметром разбиения ограничены.
В самом деле,
![]() такого что
такого что ![]() .
.
Тогда,
![]() т. е.
т. е. ![]() ограничены,
если
ограничены,
если ![]() .
.
Предположим,
что ![]() не ограничена на
не ограничена на ![]() и
и
![]() - его некоторое произвольное
разбиение. Тогда
- его некоторое произвольное
разбиение. Тогда ![]() не ограничена на одном из
отрезков разбиения, пусть, например, на
не ограничена на одном из
отрезков разбиения, пусть, например, на ![]() .
.
Запишем интегральную сумму
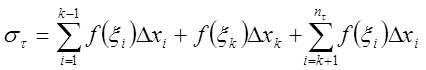 .
.
Зафиксируем точки ![]() на всех
отрезках разбиения за исключением отрезка
на всех
отрезках разбиения за исключением отрезка ![]() . На
этом отрезке рассмотрим последовательность
. На
этом отрезке рассмотрим последовательность ![]() :
: ![]() . Это можно сделать, поскольку
. Это можно сделать, поскольку ![]() не ограничена. Тогда последовательность
не ограничена. Тогда последовательность 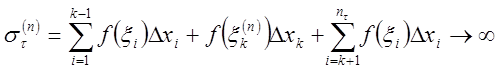 , а это противоречит тому, что интегральные
суммы
, а это противоречит тому, что интегральные
суммы ![]() для всех разбиений
для всех разбиений ![]() с достаточно малым диаметром – ограничены.
с достаточно малым диаметром – ограничены.
Следовательно, ![]() ограничена.
ограничена.
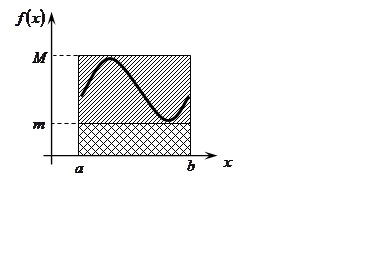
Пусть
функция ![]() ограничена на
ограничена на ![]() и
и ![]() - разбиение этого отрезка.
- разбиение этого отрезка.
Пусть
![]() и
и ![]() соответственно
точная верхняя и точная нижняя грани
соответственно
точная верхняя и точная нижняя грани ![]() на отрезке
на отрезке ![]()
Суммы:
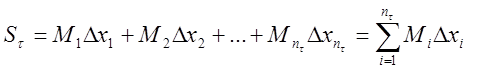 ;
;
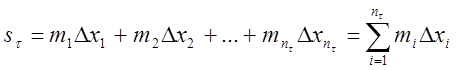
![]()
называются соответственно верхней
и нижней интегральными суммами (суммами Дарбу) функции ![]() данного разбиения
данного разбиения ![]() отрезка
отрезка
![]() . В частности, когда
. В частности, когда ![]() непрерывна на
непрерывна на ![]() , то
суммы Дарбу являются наибольшей и наименьшей из интегральных сумм, отвечающих
данному разбиению (это следует из второй теоремы Вейерштрасса), т.е.
, то
суммы Дарбу являются наибольшей и наименьшей из интегральных сумм, отвечающих
данному разбиению (это следует из второй теоремы Вейерштрасса), т.е. ![]() .
.
Заметим,
что при фиксированном разбиении суммы ![]() и
и ![]() - const, а
- const, а ![]() -
переменная в силу произвольности точек
-
переменная в силу произвольности точек ![]() на
отрезках разбиения.
на
отрезках разбиения.
Лемма: Для
любого разбиения ![]() справедливы равенства:
справедливы равенства:
![]() ;
;
![]() .
.
Доказательство:
Докажем первое из равенств.
Поскольку
![]() , то
, то ![]()
![]() :
:

Умножая эти неравенства на ![]() и суммируя по
и суммируя по ![]() ,
получим
,
получим
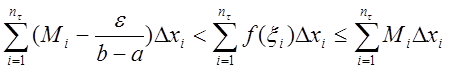 ,
,
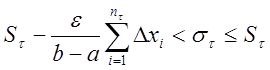 ,
,
![]() ,
,
откуда
следует, что ![]() .
.
Аналогично доказывается и второе равенство.
10. При измельчении разбиения верхние суммы не увеличиваются, а нижние не уменьшаются.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.