Математический анализ: Курс лекций (часть вторая "Интегральное исчисление функции одной переменной"), страница 2

1.5.1. Разложение рациональной дроби на простейшие

Из алгебры известно, что всякий многочлен с действительными коэффициентами можно разложить на множители с действительными коэффициентами первой и второй степени соответствующей кратности, то есть

,

причем

Линейные множители соответствуют действительным корням, а квадратные трехчлены – комплексным.

 Всякую рациональную функцию можно представить в виде рациональной дроби

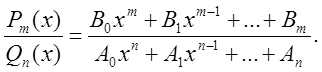
Если , то дробь неправильная, если же  правильная. Если дробь неправильная , то ее всегда можно представить в виде многочлена ( целой части ) и правильной дроби

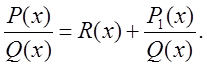
Определение: Правильные рациональные дроби вида:

I.

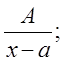
II.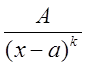  (целое положительное число);

III.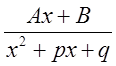 (корни знаменателя комплексные, то есть );

IV.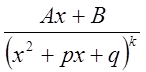 (  - целое положительное число; корни знаменателя комплексные);

называются простейшими дробями.

Теорема: Если

то правильная несократимая рациональную дробь 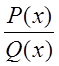 можно быть единственным образом разложена в сумму простейших дробей:

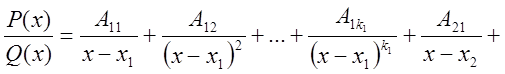
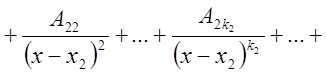
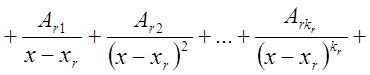
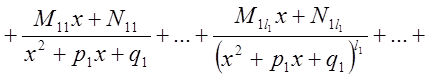
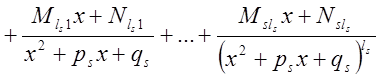
где  действительные числа.

Одним из наиболее простых методов определения коэффициентов в разложении правильной дроби на простейшие является метод неопределенных коэффициентов. Рассмотрим его на примерах.

Примеры:

1. Разложить на простейшие дроби .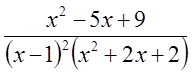

Решение:

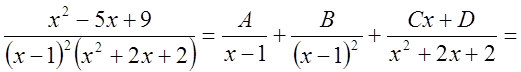
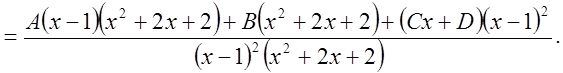
Дроби равны, знаменатели равны, следовательно, равны числители

,

.

 Пользуясь основной теоремой алгебры, можно показать, что два многочлена равны тогда и только тогда, когда равны их коэффициенты при одинаковых степенях, то есть            

                       ,

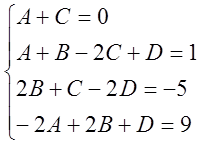
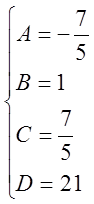поэтому

.

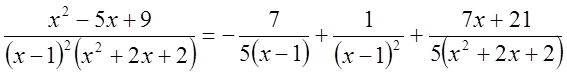2. Разложить на простейшие дроби  .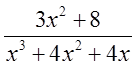

Решение:

,

.

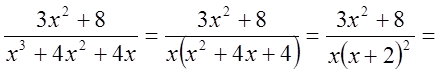
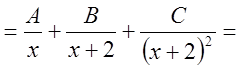
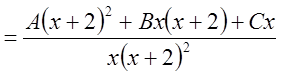              Это равенство справедливо при  любых значениях .

                                ,

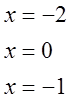
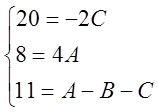
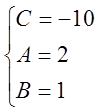поэтому

.

1.5.2. Интегрирование простейших дробей

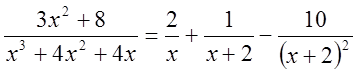I. ;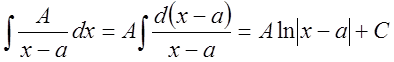

II.

, ;

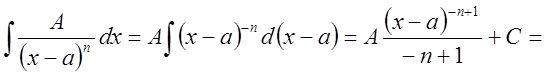
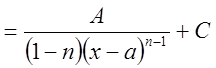III.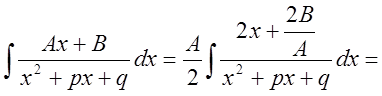

.

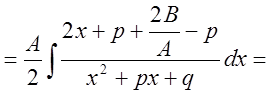
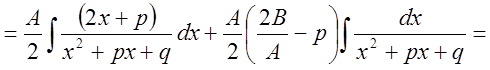
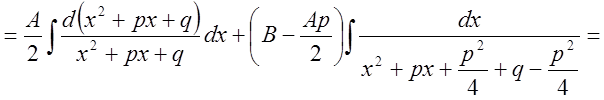
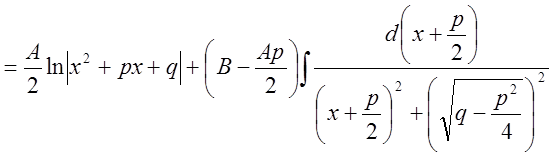Последний интеграл есть табличный и представляет собой арктангенс.

IV.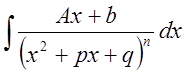

Рассмотрим сначала  .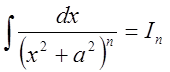

,

.

.

.

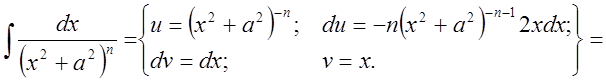
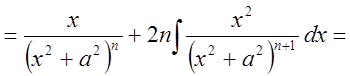
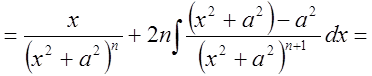
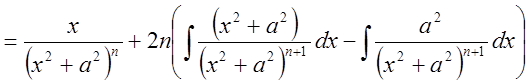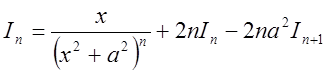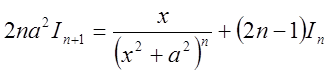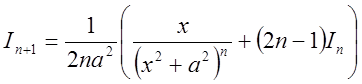Заметим, что при .

.

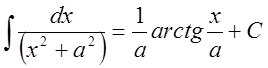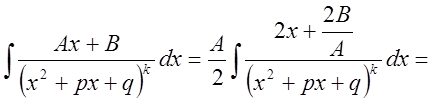
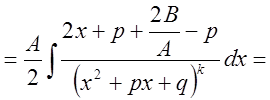
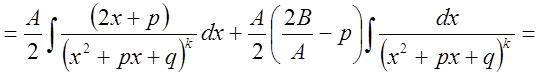
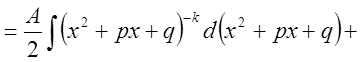
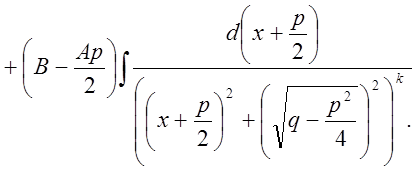
Теорема:  Всякая рациональная дробь интегрируется в элементарных функциях посредством рациональных дробей, арктангенсов и натуральных логарифмов.

1.5.3. Метод Остроградского

Интегралы от простейших дробей вида  I и II являются трансцендентными функциями.

Интеграл от дроби II, знаменатель которой есть двучлен в степени , является правильной рациональной дробью со знаменателем, равным тому же двучлену в степени .

Интеграл от дроби вида IV, знаменатель которой есть трехчлен в степени , равен сумме правильной рациональной дроби со знаменателем, равным тому же трехчлену в степени , и приводящегося к арктангенсу (трансцендентная функция).

Отсюда следует, что рациональная часть интеграла от правильной несократимой рациональной дроби 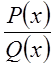 равна сумме правильных рациональных дробей , то есть представляет собой правильную рациональную дробь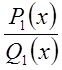, знаменатель которой имеет вид

(Можно показать, что  есть наибольший общий делитель многочленов  и ).

Сумма же простейших дробей, интегралы от которых дают трансцендентные функции, очевидно,  равна правильной рациональной дроби 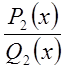, знаменатель которой равен

.

(Многочлен  может быть вычислен делением  на ).

Таким образом ,

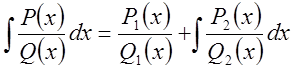 - формула Остроградского.

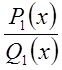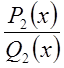              Так как дроби  и  правильные, то  можно рассматривать как многочлен с неопределенными коэффициентами степени на единицу ниже, чем , а  -  как многочлен с неопределенными коэффициентами степени на единицу ниже, чем  . Для вычисления неопределенных коэффициентов следует продифференцировать формулу Остроградского, привести результат дифференцирования к общему знаменателю и сопоставить коэффициенты при одинаковых степенях  в числителях.

Примеры:

1. Применим метод Остроградского для вычисления интеграла

.

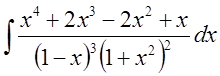Решение:

.

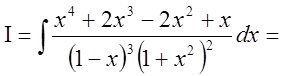
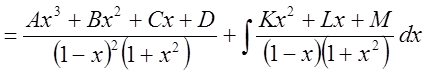Дифференцируя, получим: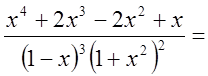

.

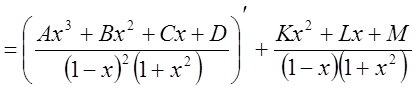Далее найдем в правой части производную, приведем правую часть к общему знаменателю.  Получим равенство двух дробей с одинаковыми знаменателями.  Следовательно, равны числители.  Приравнивая коэффициенты при одинаковых степенях  в числителях, получим систему линейных уравнений, решая которые, найдем.