(Доказательство непосредственно следует из п.п. 2 и 4 предыдущей теоремы).
Теорема: Всякая непрерывная на отрезке функция интегрируема на этом отрезке.
Доказательство:
Пусть функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() . Тогда
она ограничена и равномерно непрерывна на нем. Это означает, что
. Тогда
она ограничена и равномерно непрерывна на нем. Это означает, что![]()
![]() :
: ![]() ,
, ![]() Þ
Þ 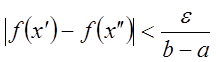 .
.
Пусть ![]() - произвольное
разбиение отрезка
- произвольное
разбиение отрезка ![]() такое, что
такое, что ![]() . Рассмотрим отрезок
. Рассмотрим отрезок ![]() . Пусть
. Пусть ![]() и
и ![]() причем
причем ![]() ,
, ![]() ,
, ![]() (по
второй теореме Вейерштрасса).
(по
второй теореме Вейерштрасса).
Тогда,
т.к. ![]() , то
, то 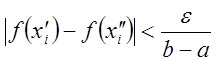
и
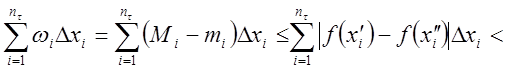
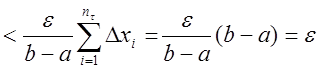 .
.
Отсюда следует, что 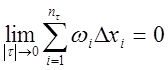 , и
функция
, и
функция ![]() интегрируема
по Риману на
интегрируема
по Риману на ![]() .
.
Теорема: Всякая монотонная на отрезке функция интегрируема на этом отрезке.
Доказательство:
Пусть функция ![]() монотонна
на отрезке
монотонна
на отрезке ![]() и для определенности будем считать, что
и для определенности будем считать, что ![]() неубывающая, и
неубывающая, и ![]() .
Очевидно,
.
Очевидно, ![]()
![]() .
.
Рассмотрим произвольное разбиение
![]() отрезка
отрезка ![]() с
диаметром
с
диаметром  , где
, где ![]() – произвольное
число.
– произвольное
число.
Очевидно, что для любого частичного отрезка ![]() разбиения
разбиения
![]()
![]() .
.
Тогда
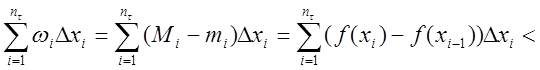
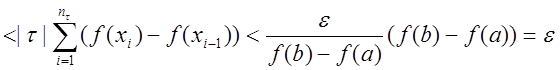 .
.
Имеем 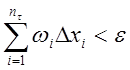 ,
, ![]()
![]() - интегрируема на
- интегрируема на ![]() .
.
Замечание: Очевидно,
что теорема верна и в случае, когда ![]() , т.к. в этом случае
, т.к. в этом случае ![]() и
и 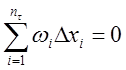 .
.
Определение: Говорят,
что множество точек числовой прямой имеет Жорданову меру ноль, если ![]() существует конечная система отрезков или
интервалов, сумма длин которых меньше
существует конечная система отрезков или
интервалов, сумма длин которых меньше![]() , покрывающая это
множество.
, покрывающая это
множество.
Определение: Говорят, что множество точек числовой прямой имеет Лебегову меру
ноль, если ![]() существует не более чем счетная система
отрезков или интервалов, сумма длин которых меньше
существует не более чем счетная система
отрезков или интервалов, сумма длин которых меньше ![]() ,
покрывающей это множество.
,
покрывающей это множество.
Теорема: (критерий
интегрируемости Лебега). Функция ![]() , ограниченная на отрезке
, ограниченная на отрезке ![]() ,
интегрируема на нем по Риману тогда и только тогда, когда множество ее точек
разрыва имеет Лебегову меру ноль.
,
интегрируема на нем по Риману тогда и только тогда, когда множество ее точек
разрыва имеет Лебегову меру ноль.
Следствие: Если
функция ![]() ограничена
на
ограничена
на ![]() и множество ее точек разрыва имеет Жорданову
меру ноль, то она интегрируема на
и множество ее точек разрыва имеет Жорданову
меру ноль, то она интегрируема на ![]() по Риману. В частности,
ограниченная на
по Риману. В частности,
ограниченная на ![]() функция, имеющая конечное число
точек разрыва, интегрируема по Риману на этом отрезке.
функция, имеющая конечное число
точек разрыва, интегрируема по Риману на этом отрезке.
Доказательство:
Докажем, что функция ![]() , имеющая конечное число точек разрыва
, имеющая конечное число точек разрыва ![]() на
на ![]() интегрируема
по Риману.
интегрируема
по Риману.
Зададим произвольное ![]() . Так
как точек разрыва конечное число, то покроем их конечным числом,
непересекающихся интервалов
. Так
как точек разрыва конечное число, то покроем их конечным числом,
непересекающихся интервалов ![]() , сумма длин которых меньше чем
, сумма длин которых меньше чем 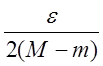 ,
,
где
![]()
![]() .
.
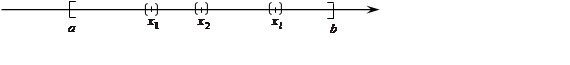
Точки
отрезка, не входящие в ![]() , образуют множество:
, образуют множество: 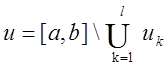 - объединение конечного числа
непересекающихся отрезков. На каждом таком отрезке
- объединение конечного числа
непересекающихся отрезков. На каждом таком отрезке ![]() непрерывна, а следовательно (по теореме Кантора) и
равномерно непрерывна. Выберем на каждом из этих отрезков разбиения такие, что
колебание функции
непрерывна, а следовательно (по теореме Кантора) и
равномерно непрерывна. Выберем на каждом из этих отрезков разбиения такие, что
колебание функции ![]() на
каждом частичном отрезке разбиения меньше, чем
на
каждом частичном отрезке разбиения меньше, чем 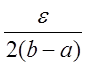 .
Тогда, объединяя все эти разбиения и точки
.
Тогда, объединяя все эти разбиения и точки ![]() ,
получим разбиение
,
получим разбиение ![]() всего отрезка
всего отрезка ![]() .
.
Для этого разбиения

где
сумма 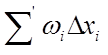 - распространяется на интервалы
- распространяется на интервалы ![]() , а
, а ![]() - на
остальные слагаемые.
- на
остальные слагаемые.
Тогда имеем:

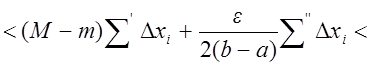
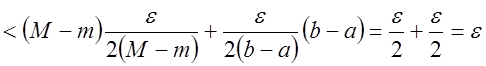 .
.
Таким образом, ![]()
![]() :
: 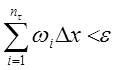
![]()
![]() интегрируема
на
интегрируема
на ![]() по Риману.
по Риману.
Обозначим
через ![]() множество всех функций, интегрируемых по Риману на
множество всех функций, интегрируемых по Риману на ![]() .
.
10.Если ![]() ,
то
,
то ![]() где
где ![]() ,
причем
,
причем
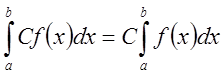 ,
,
т. е. постоянный множитель можно выносить за знак интеграла.
Доказательство:
Для
любого разбиения ![]() отрезка
отрезка ![]() и
произвольного выбора точек
и
произвольного выбора точек ![]() имеет место равенство:
имеет место равенство:
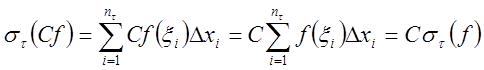 ,
,
где![]() ,
,
![]() - интегральные суммы функций
- интегральные суммы функций ![]() и
и ![]() при
одном и том же выборе промежуточных точек
при
одном и том же выборе промежуточных точек ![]() .
.
Переходя
к пределу при ![]() , получим
, получим
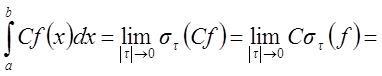
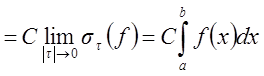 .
.
Интеграл в правой части равенства существует, значит, существует и интеграл в левой части.
20.
Пусть ![]() и
и ![]() ,
тогда
,
тогда ![]() , причем
, причем
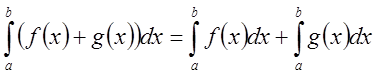 ,
,
то есть интеграл от суммы равен сумме интегралов.
Доказательство:
Для
любого разбиения ![]() отрезка
отрезка ![]() и
произвольного выбора точек
и
произвольного выбора точек ![]() имеет место равенство:
имеет место равенство:

![]() .
.
Переходя
к пределу при ![]() , получим
, получим
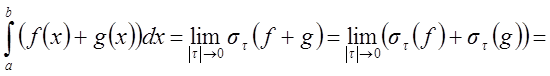

Интеграл в правой части равенства существует, значит, существует и интеграл в левой части.
Следствие: (свойство линейности)
Если
![]() , то любая их линейная комбинация
, то любая их линейная комбинация
![]() ,
,
причем:
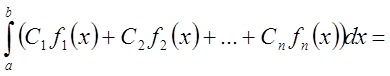
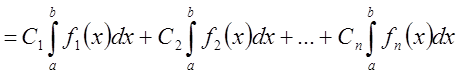 .
.
30. Пусть
![]() и
и ![]() ,
тогда
,
тогда ![]() .
.
Доказательство:
Из
![]()
![]()
![]() отрезка
отрезка ![]()
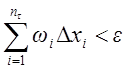 .
.
Рассмотрим
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.