Приклади розв'язання задач до контрольної роботи 4
Задача
1.Знайти невизначений інтеграл ![]()
Розв'язання.
Застосуємо
правило інтегрування частинами: ![]()
![]()
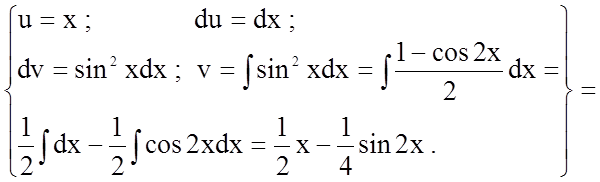
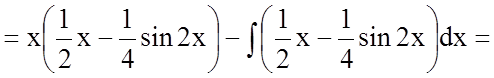
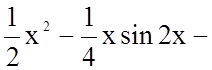
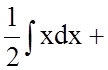
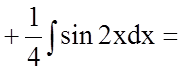
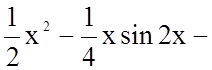
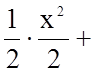
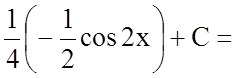
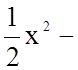
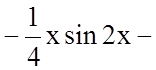
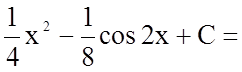
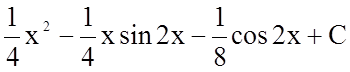 .
.
Задача
2. Обчислити
визначений інтеграл 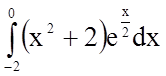
Розв'язання.
Застосуємо правило інтегрування частинами у визначеному інтегралі:
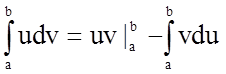 .
.
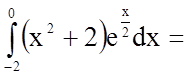
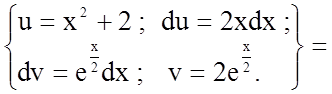
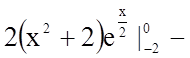
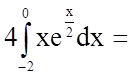
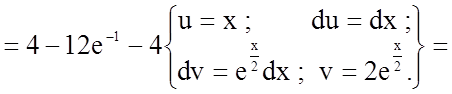
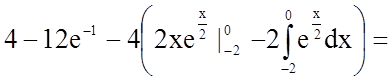
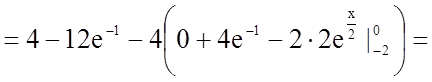
![]()
![]()
![]() .
.
Задача 3. Знайти невизначений інтеграл 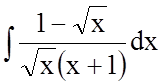
Розв'язання.
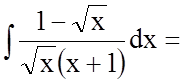
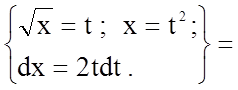
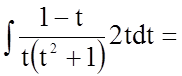
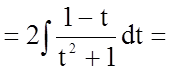
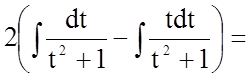
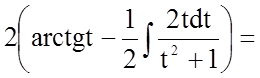
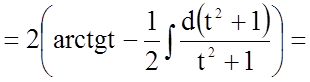
![]()
![]() .
.
Задача
4. Обчислити
визначений інтеграл 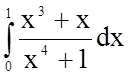 .
.
Розв'язання.
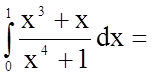
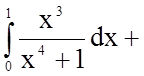
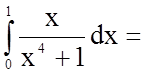
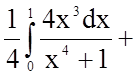
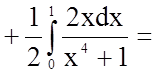

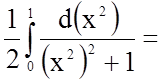
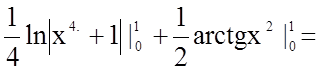
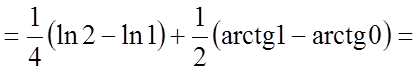
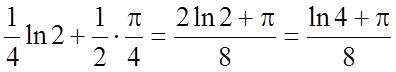 .
.
Задача 5. Знайти невизначений інтеграл 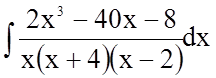
Розв'язання.
Підінтегральна функція є неправильний раціональний дріб (степінь чисельника дробу не менша за степінь його знаменника). Виділимо цілу частину цього дробу.
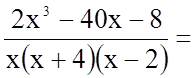
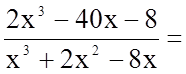
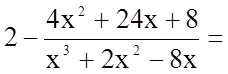
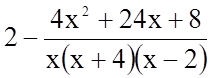 .
.
Маємо 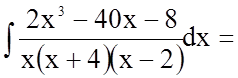
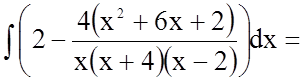
![]()
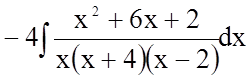 .
.
В останньому інтегралі підінтегральна функція є правильний дріб. Розкладемо його на елементарні дроби методом невизначених коефіцієнтів.
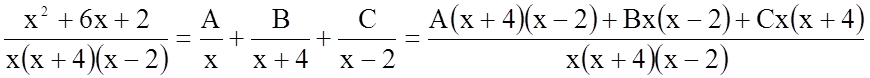 .
.
Оскільки в цій рівності початковий і кінцевий дроби дорівнюють один одному і мають однакові знаменники, то і їхні чисельники дорівнюють один одному.
![]() .
.
Ця рівність виконується для будь-яких значень ![]() .
.
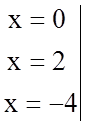
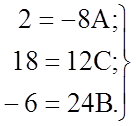
![]()
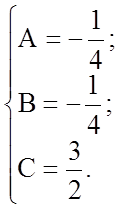
Таким чином, маємо
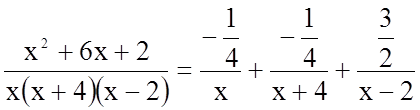 .
.
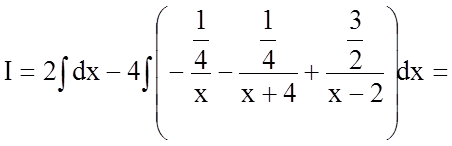
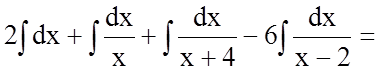
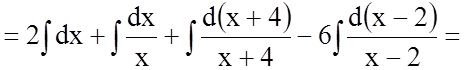
![]() .
.
Задача 6. Знайти невизначений інтеграл 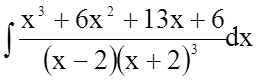
Розв'язання.
Підінтегральна функція являє собою правильний раціональний дріб (степінь чисельника менший за степінь знаменника). Розкладемо цей дріб на елементарні дроби методом невизначених коефіцієнтів.
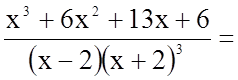
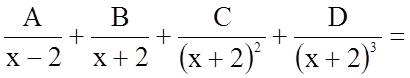
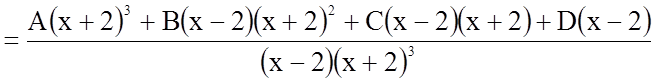 .
.
Звідси маємо
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() .
.
Маємо рівність двох многочленів. Два многочлени дорівнюють один одному тоді і тільки тоді, коли дорівнюють один одному їхні коефіцієнти при однакових степенях. Тобто
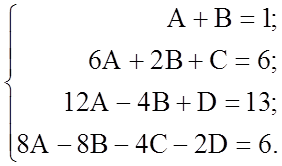
Розв'язавши цю систему рівнянь, одержимо
![]()
Таким чином
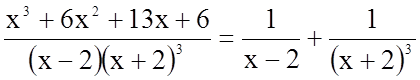 .
.
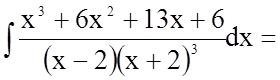
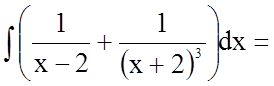
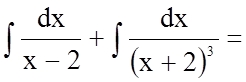
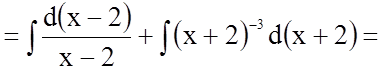
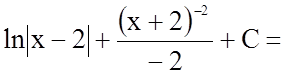
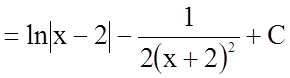 .
.
Задача 7. Знайти невизначений інтеграл 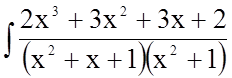 .
.
Розв'язання.
Підінтегральна функція є правильний раціональний дріб. Розкладемо його на елементарні дроби, як і в попередніх задачах, за допомогою методу невизначених коефіцієнтів.
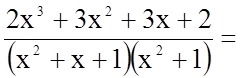
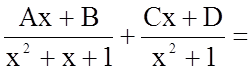
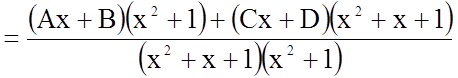 .
.
Звідси маємо
![]() ;
;
![]() ;
;
![]() .
.
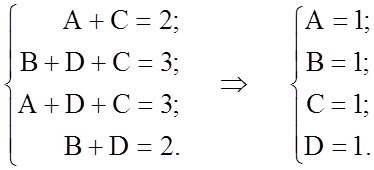
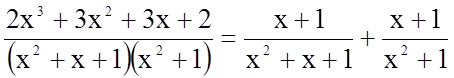 .
.
Тому
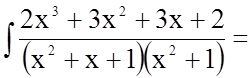
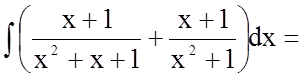
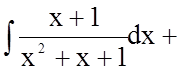
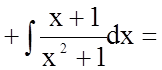
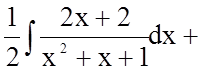
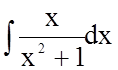
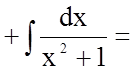
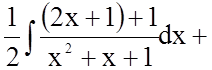
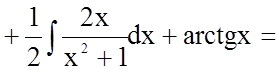
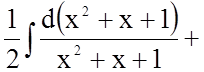
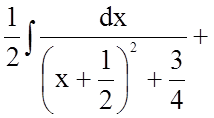
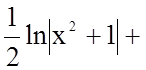
![]()
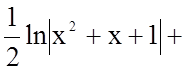
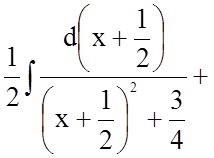
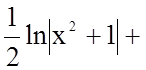
![]()
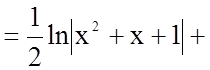
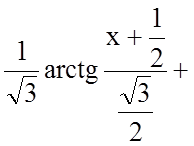
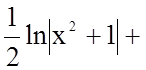
![]()
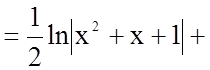
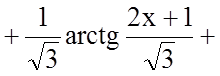
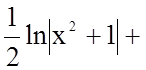
![]() .
.
Задача 8. Обчислити визначений інтеграл 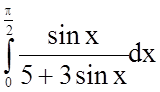 .
.
Розв'язання.
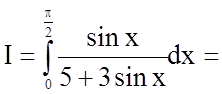
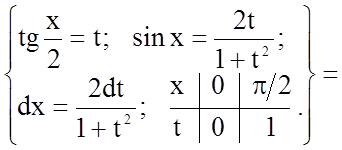
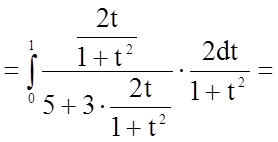
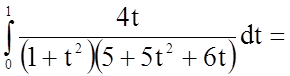
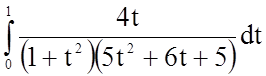 .
.
Розкладемо підінтегральну функцію (правильний раціональний дріб) на елементарні дроби.
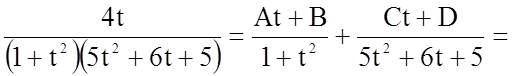
=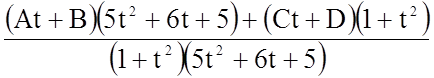 .
.
Звідси маємо
![]() ;
;
![]() ;
;
![]() .
.
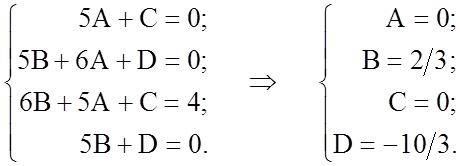
Таким чином,
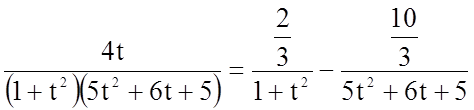 .
.
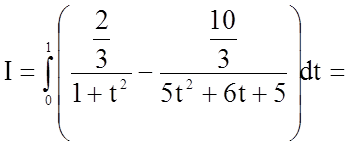
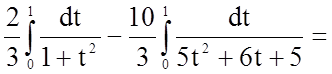

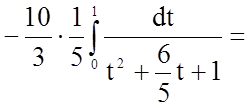
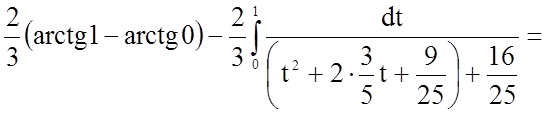
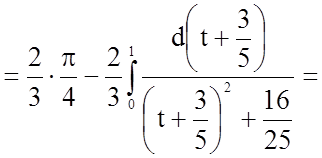
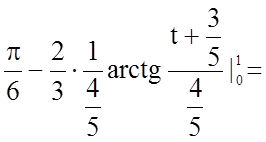
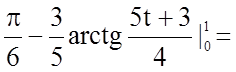
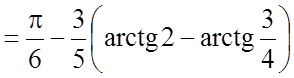 .
.
Задача 9. Обчислити визначений інтеграл 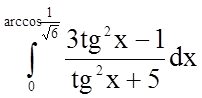
Розв'язання.
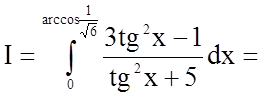
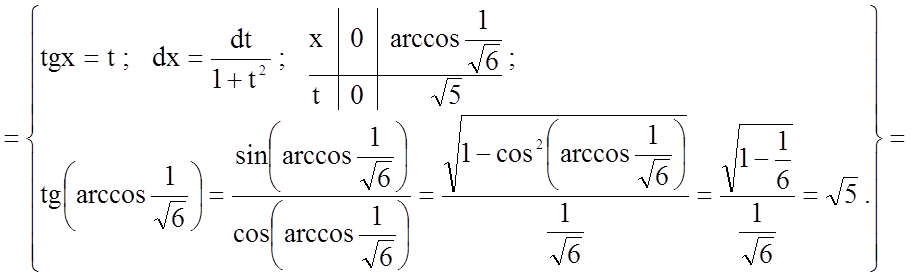
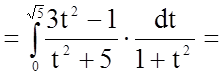
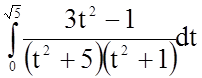 .
.
Розкладемо підінтегральну функцію на елементарні дроби.
 .
.
Звідси маємо
![]() ;
;
![]() ;
;
![]() ;
;
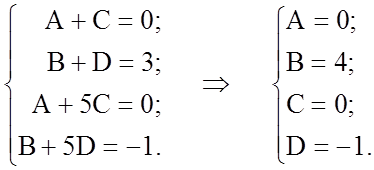
Тому 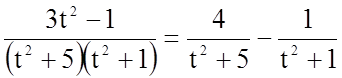 .
.
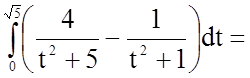
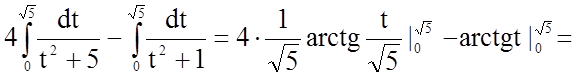
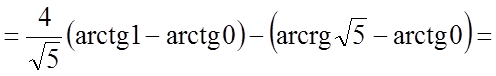
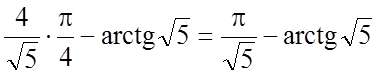 .
.
Задача 10. Обчислити визначений інтеграл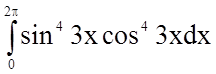
Розв'язання.

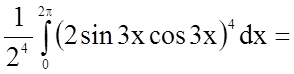
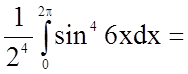
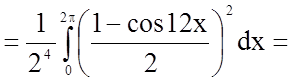
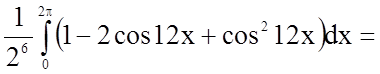
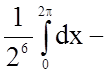
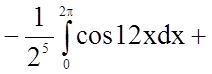
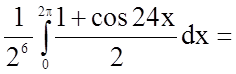
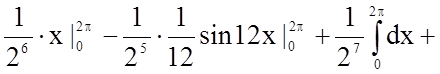
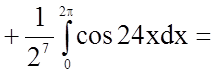
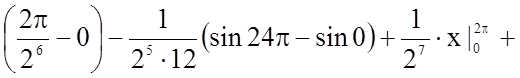
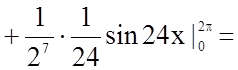
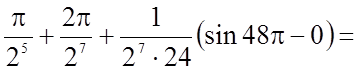
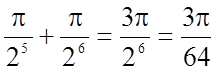 .
.
Задача 11. Обчислити визначений інтеграл 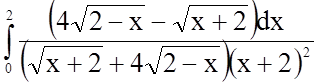
Розв'язання.
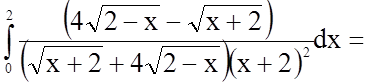
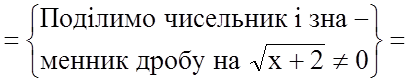
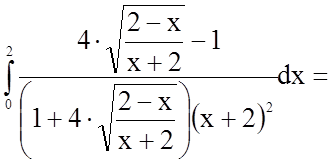

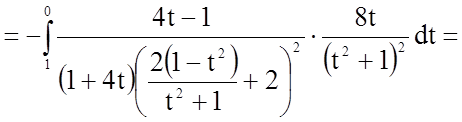
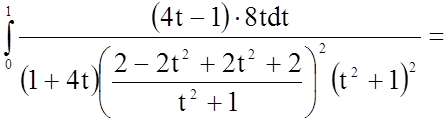
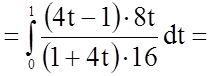
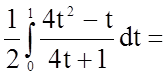
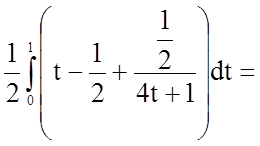
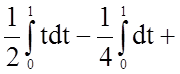
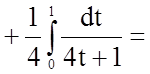
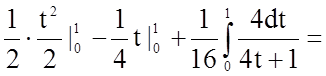
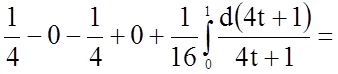
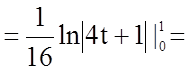
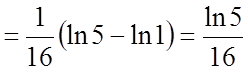 .
.
Задача 12. Обчислити визначений інтеграл 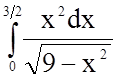
Розв'язання.
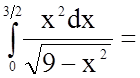
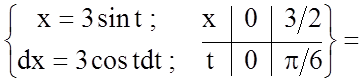
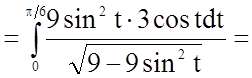
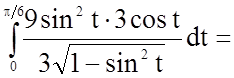
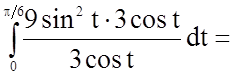
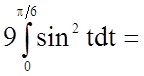
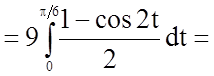
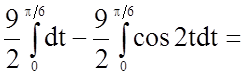
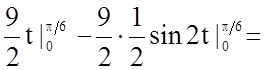
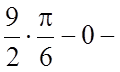
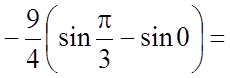
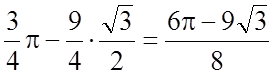 .
.
Задача 13. Знайти невизначений інтеграл 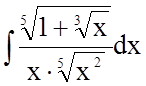
Розв'язання.
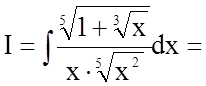
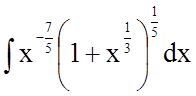 .
.
Маємо інтеграл виду ![]() ,
тобто інтеграл від диференціального біному. У нас
,
тобто інтеграл від диференціального біному. У нас 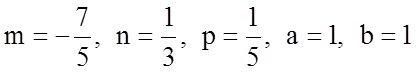 .
Бачимо, що
.
Бачимо, що ![]() ;
;
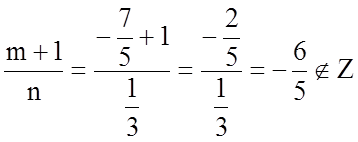 ;
; 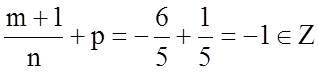 .
.
У цьому випадку треба зробити заміну 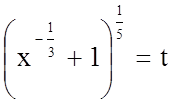 .
.
Тоді маємо: 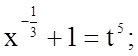
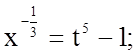
![]()
![]() .
.
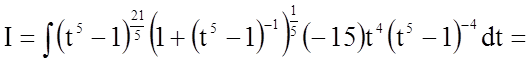

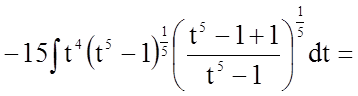
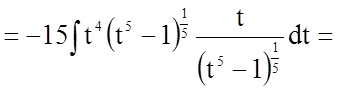
![]()
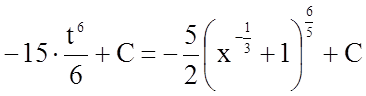 .
.
Задача 14. Обчислити площу фігури, обмеженої графіками
функцій ![]() та
та ![]()
Розв'язання.
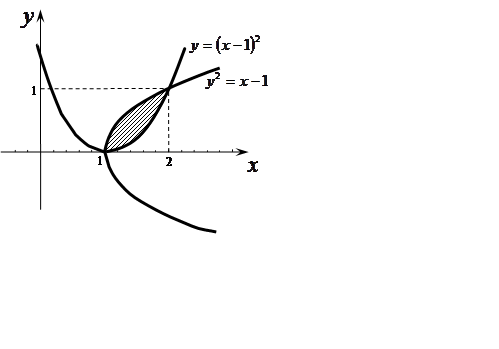
Щоб знайти шукану площу, скористаємося формулою
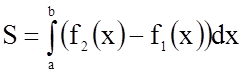 .
.
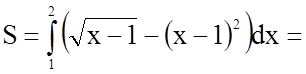
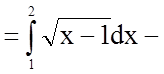
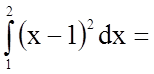
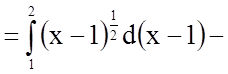
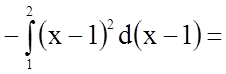
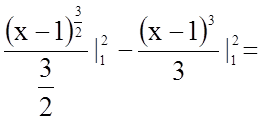
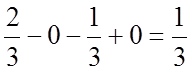 .
.
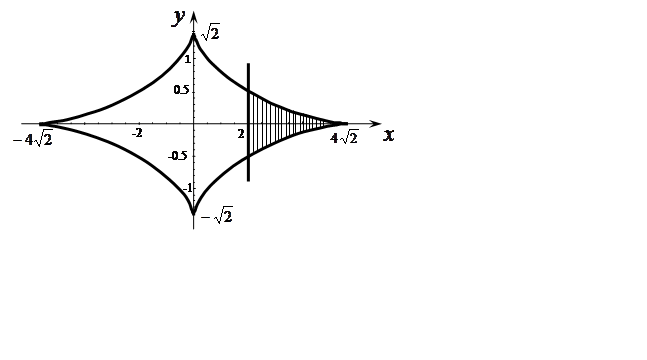
Задача 15. Обчислити площу фігури, обмеженої лініями, що задані рівняннями
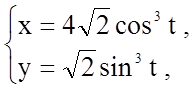
![]()
Розв'язання.
Знайдемо
координати точки ![]() . Очевидно,
. Очевидно, ![]() .
.
Тоді ![]()
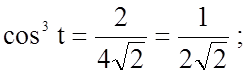
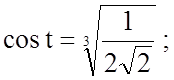
 |
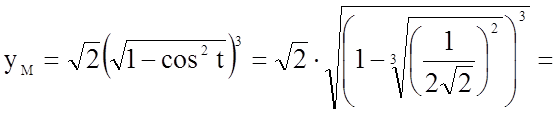
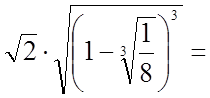
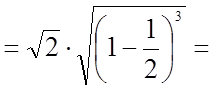
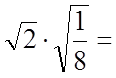
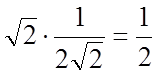 .
.
Таким чином, 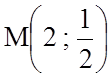 .
.
Точці ![]() відповідає
значення параметру
відповідає
значення параметру 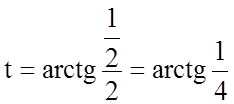 .
.
Фігура, площу якої ми знаходимо, симетрична
відносно осі ![]() . Тому знайдемо площу половини фігури, а
потім подвоїмо її. Для знаходження площі скористаємося формулою
. Тому знайдемо площу половини фігури, а
потім подвоїмо її. Для знаходження площі скористаємося формулою 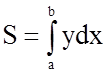 , враховуючи, що
, враховуючи, що ![]() і
і
![]() виражаються через параметр
виражаються через параметр ![]() .
.
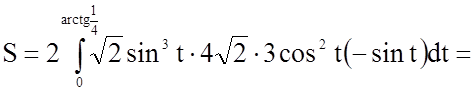
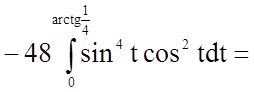
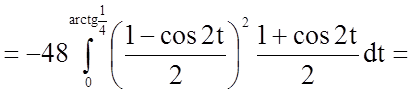
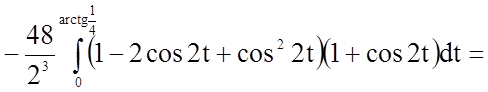
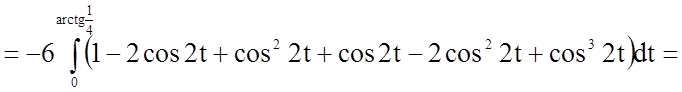
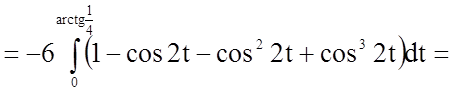
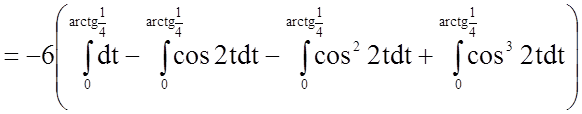 .
.
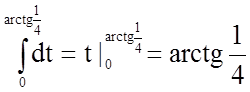 ;
;
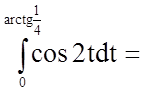
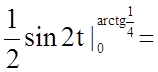
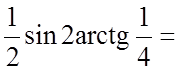
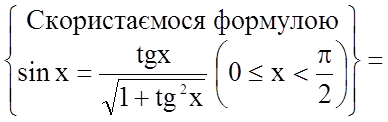
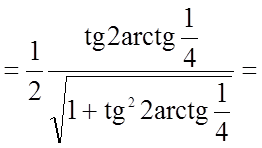
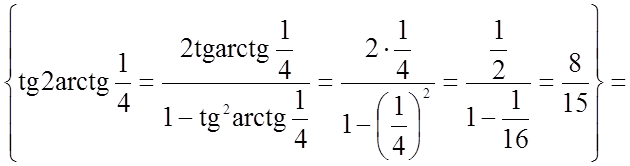
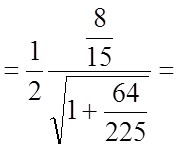
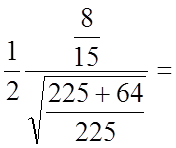
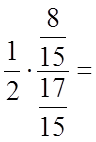
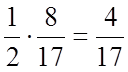 ;
;
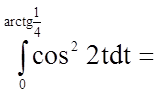
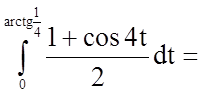
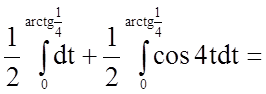
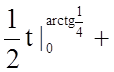
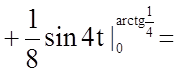
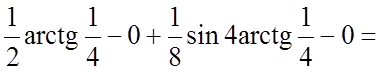
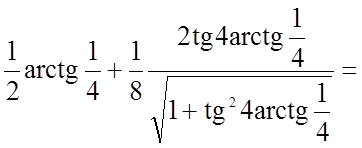
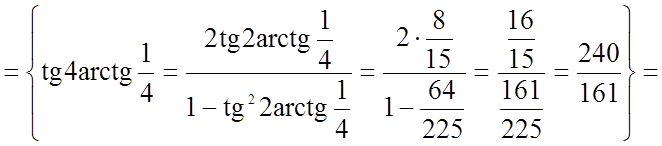
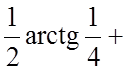
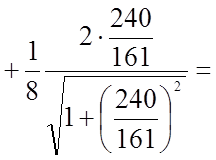
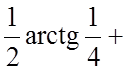
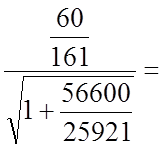
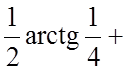
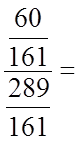
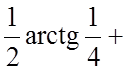
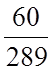 .
.
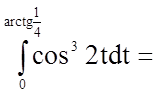
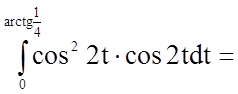
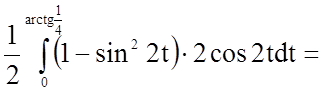
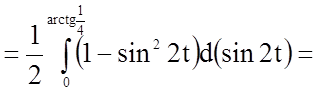
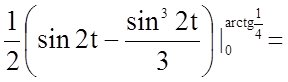
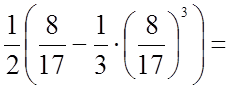
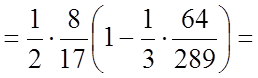
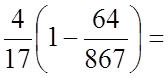
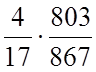 .
.
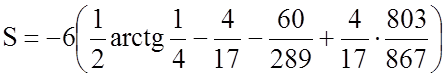 .
.
Задача 16. Обчислити площу фігури, обмежену лініями,
заданими рівняннями в полярних координатах: ![]()
Розв'язання.
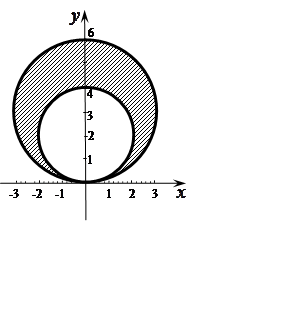 Скористаємося формулою
Скористаємося формулою 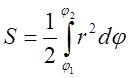 .
.
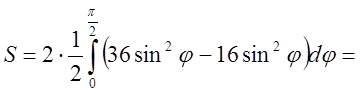
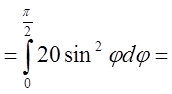
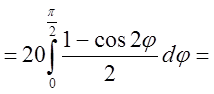
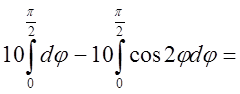
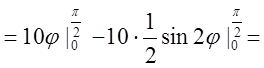
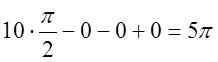 .
.
Задача 17. Знайти довжину дуги кривої, заданої рівнянням
в прямокутній системі координат: ![]()
Розв'язання.
Довжина дуги кривої, заданої в явному вигляді ![]() , в прямокутній системі координат
обчислюється за формулою
, в прямокутній системі координат
обчислюється за формулою 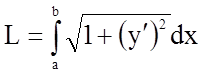 .
.
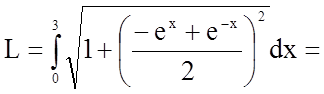
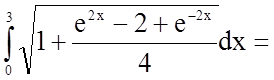
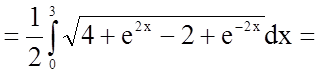
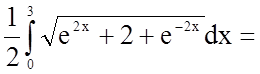
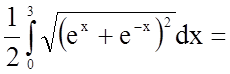
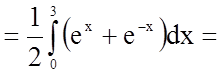
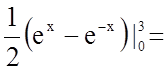
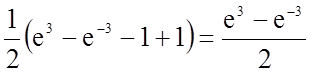 .
.
Задача 18. Обчислити довжину дуги кривої, заданої
параметричними рівняннями 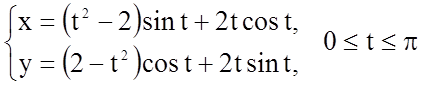
Розв'язання.
Довжина дуги кривої, заданої параметричними
рівняннями 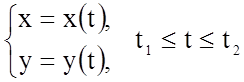 обчислюється за формулою
обчислюється за формулою 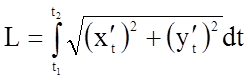 .
.
![]()
![]()
![]() ;
;
![]()
![]()
![]() ;
;
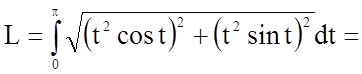
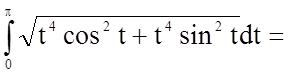
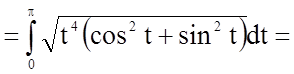
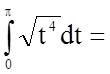
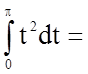
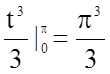 .
.
Задача 19. Обчислити довжину дуги кривої, заданої рівнянням в полярних
координатах: 
Розв'язання.
Довжина дуги кривої, заданої рівнянням в
полярних координатах, обчислюється за формулою 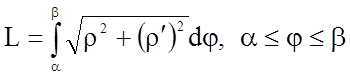 .
.
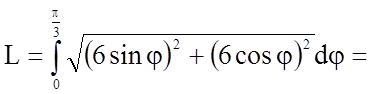
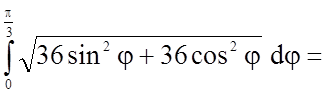
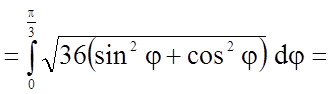
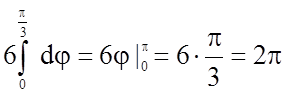 .
.
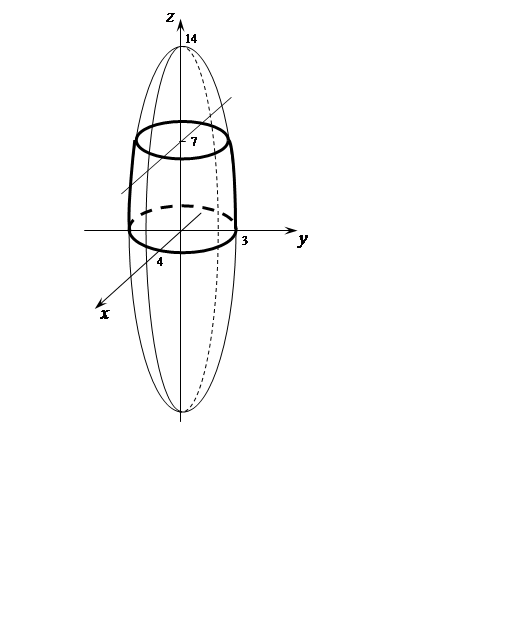
Задача 20. Обчислити об'єм тіла, обмеженого поверхнями 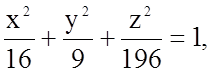
![]()
Розв'язання.
Якщо ![]() – площа
поперечного перерізу тіла площиною, перпендикулярною осі
– площа
поперечного перерізу тіла площиною, перпендикулярною осі ![]() (при довільному
(при довільному ![]() ),
),
![]() – площини, між якими міститься тіло, то
об'єм тіла обчислюється за формулою
– площини, між якими міститься тіло, то
об'єм тіла обчислюється за формулою 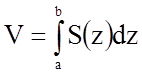 .
.
В поперечному перерізі маємо частину площини, обмежену еліпсом
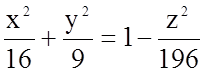 , або
, або
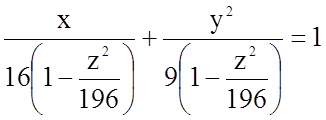 .
.
Як відомо, площа, обмежена еліпсом 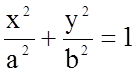 , дорівнює
, дорівнює ![]() . У
нашому випадку
. У
нашому випадку
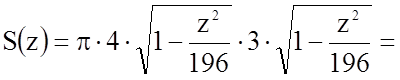
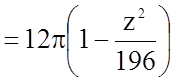 .
.
Тому маємо:
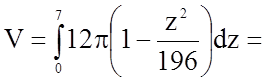
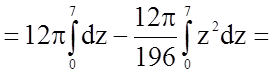
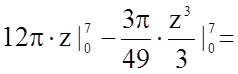
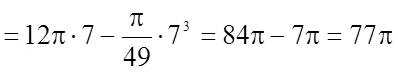 .
.
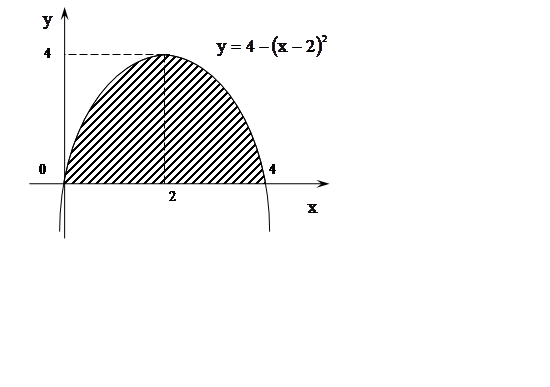
Задача 21. Обчислити об'єми тіл, утворених обертанням фігури,
обмеженої графіками функцій ![]() навколо осі
навколо осі ![]() і навколо осі
і навколо осі ![]() .
.
Розв'язання.
 Об'єми тіл, утворених обертанням криволінійної
трапеції, обмеженої кривою
Об'єми тіл, утворених обертанням криволінійної
трапеції, обмеженої кривою ![]() , віссю
, віссю ![]() та двома вертикалями
та двома вертикалями ![]() навколо осей
навколо осей ![]() і
і ![]() , виражаються відповідно формулами:
, виражаються відповідно формулами:
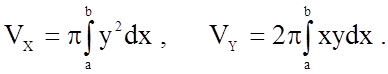
У нашому випадку
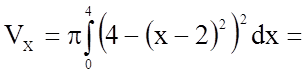
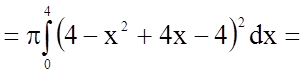
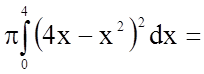
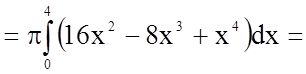
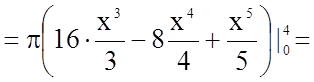
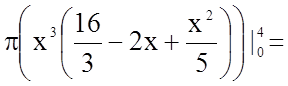
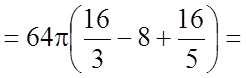
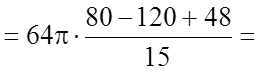
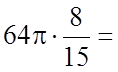
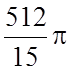 .
.
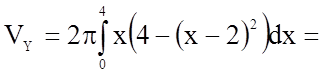
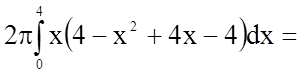
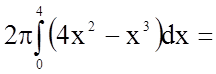
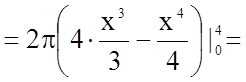
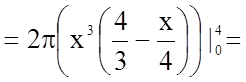
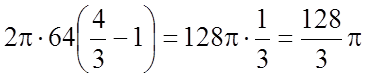 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.