Приклади розв'язання задач до контрольної роботи № 7 "Функції декількох змінних"

Приклади розв'язання задач до контрольної роботи № 7

Задача 1. Знайти й побудувати (зобразити) область визначення функції .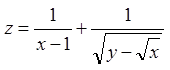

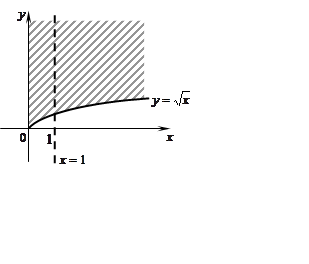Розв'язання.

            .

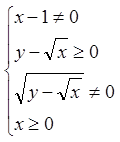
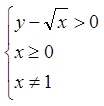
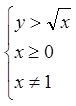Задача 2. Обчислити границю функції .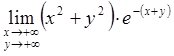

Розв'язання.При ,  має місце нерівність

.

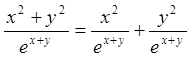
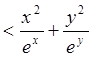Тоді

.

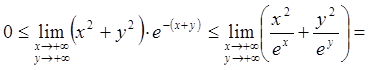
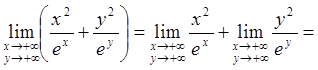
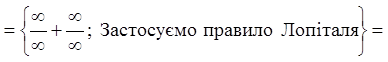
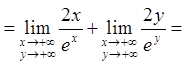
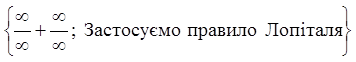
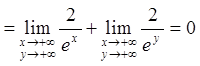Маємо .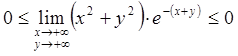

Звідси .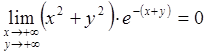

Задача 3. Показати, що функція 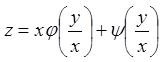 задовольняє рівнянню

.

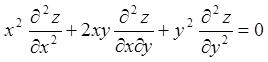Розв'язання.Позначимо 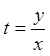, тоді .

                              

;

            

                                    ;

                            

                                ;

                               ;

.

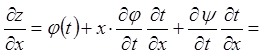
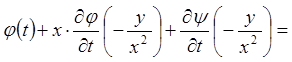
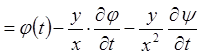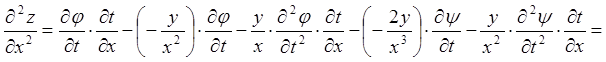
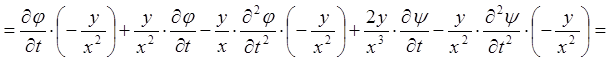
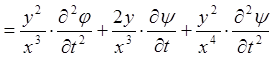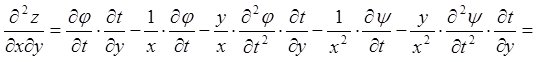
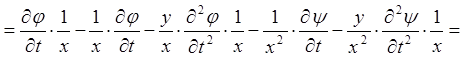
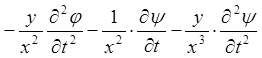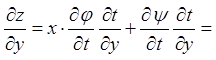
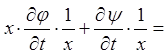
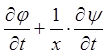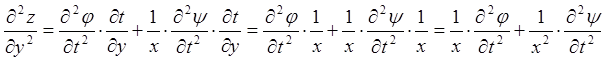            Підставимо одержані вирази для частинних похідних в ліву частину рівняння

.

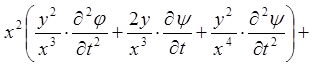
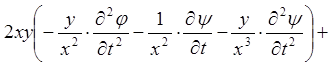
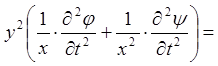
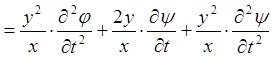
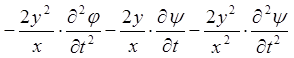
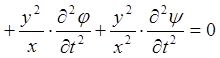            Таким чином, функція 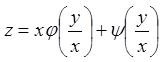 задовольняє даному в умові рівнянню.

Задача 4. Знайти частинну похідну 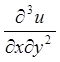, якщо .

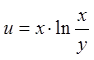Розв'язання.

;

                                                        ;

                                                      .

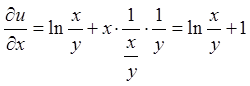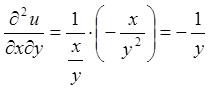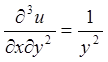Задача 5. Замінюючи приріст функцій її диференціалом, обчислити наближено .

Розв'язання. Нам треба знайти значення функції  в точці .

Скористаємося тим, що , або

;

.

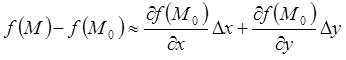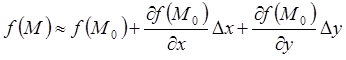            В якості  візьмемо точку 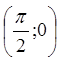 близьку до даної точки . Тоді

,       ;

,                  ;

.

;       ;

;       ;

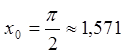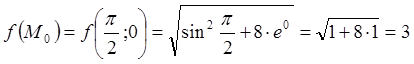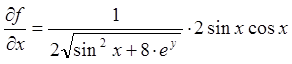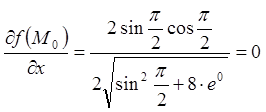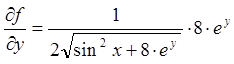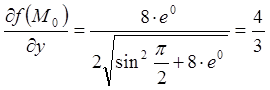Маємо

.

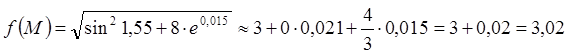Задача 6. Знайти повні диференціали першого і другого порядку від функції .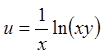

Розв'язання.

;

;

;

                               ;

                             

;

                             ;

                              ;

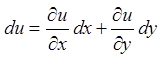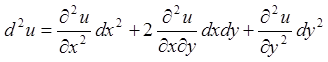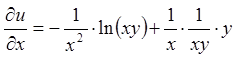
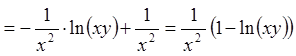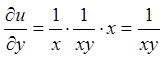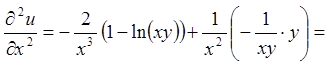
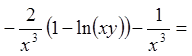
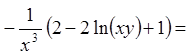
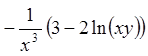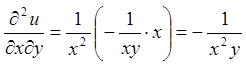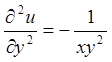Маємо

;

.

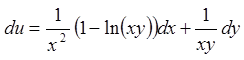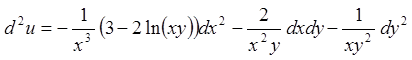Задача 7. Знайти повні диференціали першого і другого порядку від складної функції  ( - незалежні змінні).

Розв'язання. Позначимо , , маємо , де , .

;

.

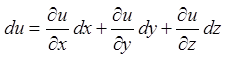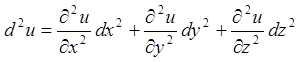
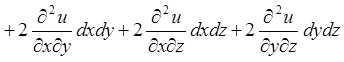Знайдемо частинні похідні першого і другого порядків.

                     ;

                     ;

                     ;

                     ;

                    

;

                     ;

                     ;

                     ;

                    

.

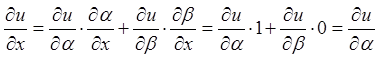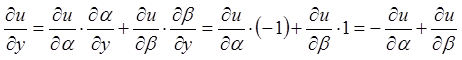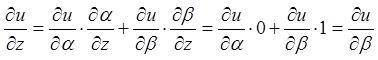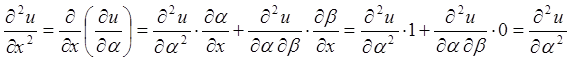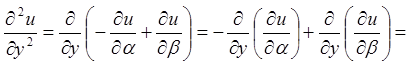
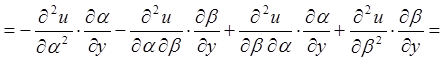
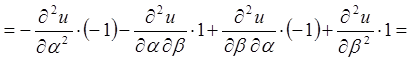
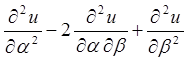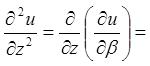
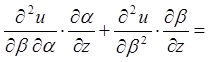
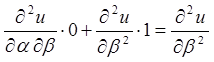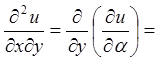
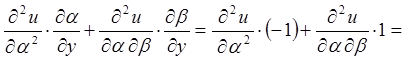
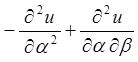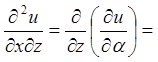
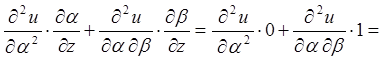
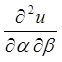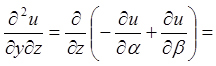
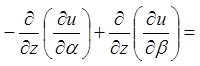
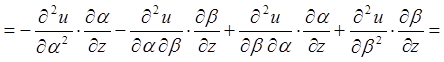
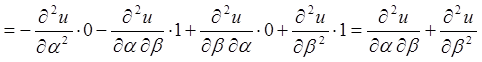Тоді

                                            ;

                                          

.

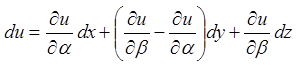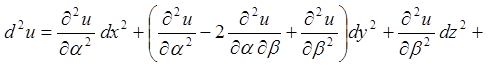
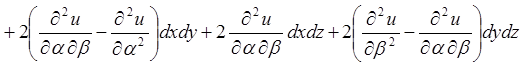Задача 8. Для функції 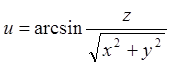 знайти градієнт в точці  і похідну в точці  за напрямком вектора ; , .

Розв'язання.

1) Знайдемо градієнт функції в точці .

.

;          ;

;          ;

                          

;          ;

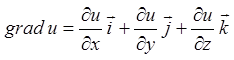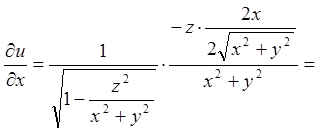
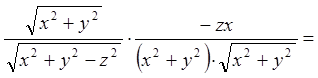
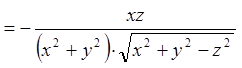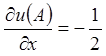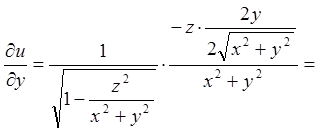
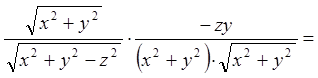
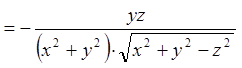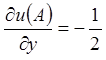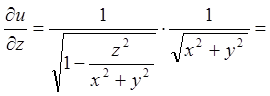
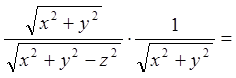
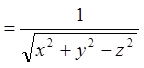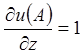Тоді градієнт функції в точці  .

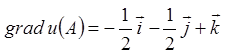2) Знайдемо похідну функції  в точці  за напрямком вектора .

;

.

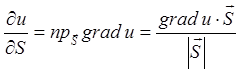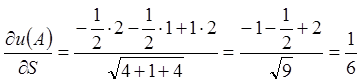Задача 9. Знайти похідну  функції заданої неявно .

Розв'язання. Похідна неявної функції , заданої за допомогою рівняння , де  - диференційована функція змінних  і , може бути обчислена за формулою

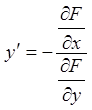 при умові .

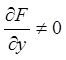            У нас , тому

;       ;

.

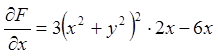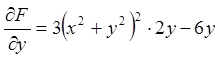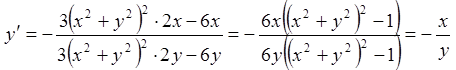Задача 10. Знайти частинні похідні ,  функції  заданої неявно .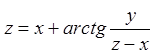

Розв'язання. Частинні похідні неявної функції , заданої за допомогою рівняння , де  - диференційована функція змінних , , , можуть бути обчислені за формулами

,       .

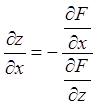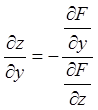            У нас 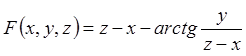, тому

;

;

;

;

.

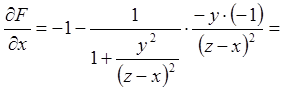
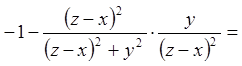
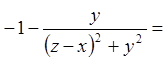
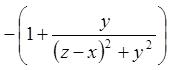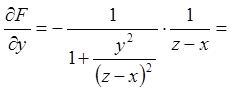
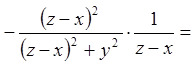
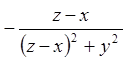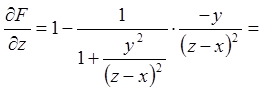
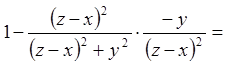
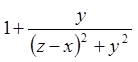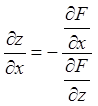
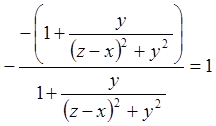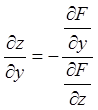
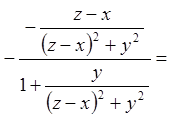
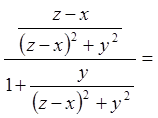
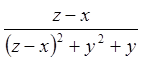Задача 11. Написати рівняння дотичної площини і рівняння нормалі до поверхні  в точці .

Розв'язання.Якщо поверхня задана рівнянням  і в точці  частинні похідні , ,  скінченні і одночасно не дорівнюють нулю, то рівняння дотичної площини до поверхні в точці  має вигляд

,

а рівняння нормалі до поверхні в тій же точці – .

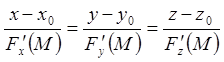            У нас , тому

,  ;      ,  ;     ,  , і

;

;

;

 - рівняння дотичної площини;

;

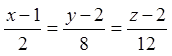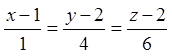 - рівняння нормалі.

Задача 12. Дослідити на екстремум функцію .

Розв'язання. Знайдемо стаціонарні точки функції.

;       ;

              

            .

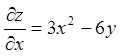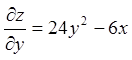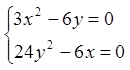
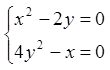
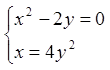
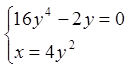
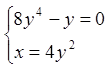
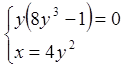
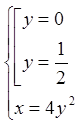
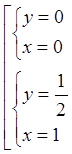            Маємо дві стаціонарні точки  і .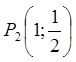

,   ,   ;

.

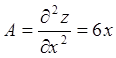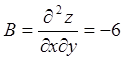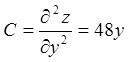            1) Для точки : . В точці  немає екстремуму.

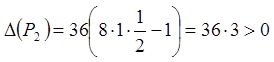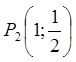            2) Для точки : , . В точці  функція має екстремум.

.

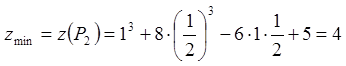Задача 13. Знайти умовні екстремуми функції , якщо  і  зв’язані рівнянням .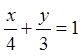

Розв'язання. Складемо функцію Лагранжа

.

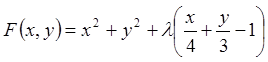            Маємо 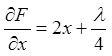,  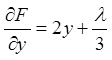. Необхідні умови екстремуму функції Лагранжа дають систему

      .

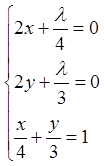
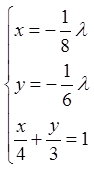            Підставивши  і  з перших двох рівнянь системи в третє рівняння, одержимо

;   ;   ;   .

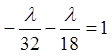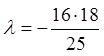            Тоді 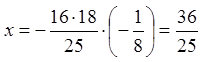,  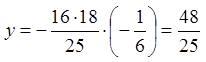. Маємо точку .

,   ,   ,   ; , .

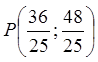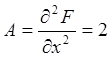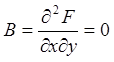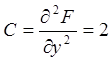            В точці  функція  має умовний мінімум.

.

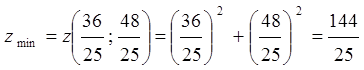Задача 14. Знайти найбільше і найменше значення функції  в області : .

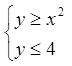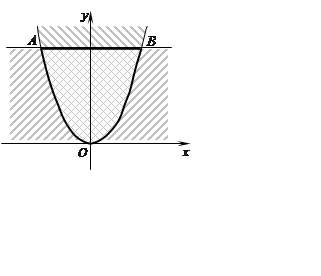Розв'язання. Зобразимо область .

Неперервна в області  функція  досягає свої найбільше і найменше значення або в точках екстремуму всередині цієї області, або на межі області.

            Знайдемо стаціонарні точки даної функції.

,   ;

               

                  .

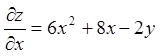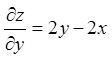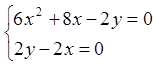
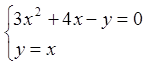
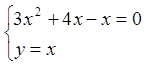
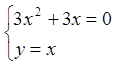
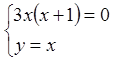
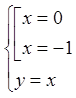
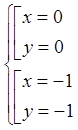            Маємо дві точки  і . Точка  не належить області , а точка  лежить на межі області. Дослідимо функцію на межі області .

            1) На відрізку  маємо , тому , де .

            Знаходимо найбільше і найменше значення цієї функції на відрізку .

,          ,

                                                                                       ,

                                                                                         , .

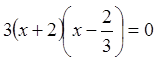
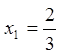            В середині відрізка маємо одну критичну точку 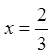, їй відповідає точка 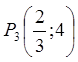. На відрізку  функція приймає свої найбільше і найменше значення або в точці , або на кінцях відрізку в точках  і .

;

;

.

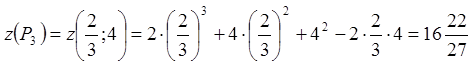            2) На дузі  маємо , тому , де .

,        ,

                                                                                     ,

                                                                                       .

            На відрізку  маємо одну критичну точку ; на дузі  їй відповідає точка .

.

            Співставляючи одержані результати, заключаємо, що найбільше значення функція  в області  приймає в точках  і : , а найменше – в точці : .

Задача 15. Знайти точку трикутника з вершинами , , , сума квадратів відстаней якої до його вершин має найбільше значення.

Розв'язання.

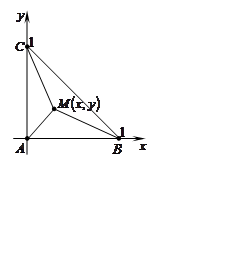
Нехай  - довільна точка трикутника , а  - сума квадратів відстаней від точки  до вершин трикутника.

Тоді

.

            Знайдемо найбільше значення функції  в області, обмеженій трикутником , тобто в області

:     .

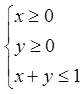            Прийшли до задачі, аналогічній задачі 14.

Маємо

;       ;

            .

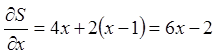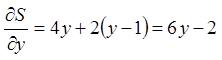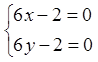
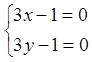
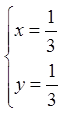            Маємо точку 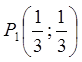, що лежить всередині трикутника .

.

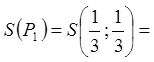
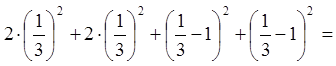
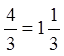            Дослідимо функцію на межі області .

1) На відрізку  маємо , тому , де .

;         .

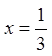            Маємо точку 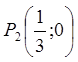, що лежить всередині відрізку .

.

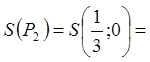
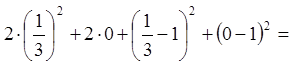
            Значенням  і  відповідають точки  і .

;

.

2) На відрізку  маємо , тому , де .

;         .

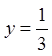            Маємо точку 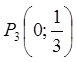, що лежить всередині відрізку .

.

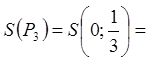
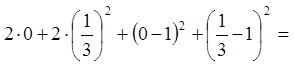
            Значенням  і  відповідають точки  і .

;

3) На відрізку  маємо , тому

, де .

;         .

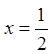            Значенню 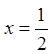 відповідає точка 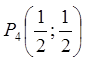, що лежить на стороні трикутника

.

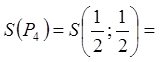
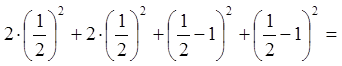
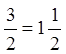            Значенням  і  відповідають точки  і , значення функції  в яких вже знайдені.

            Співставляючи одержані результати, заключаємо, що найбільше значення функції  в трикутнику  приймає в точках  і

.