Числовые ряды. Знакопеременные ряды. Функциональные ряды. Приложение рядов

Лекция №12. Числовые ряды

В приложениях математики в экономике приходится рассматривать суммы, составленные из бесконечного множества слагаемых. Из теории действительных чисел известно лишь, что означает сумма любого конечного числа чисел. Задача суммирования бесконечного множества слагаемых, а также задача представления функций в виде рядов решается в теории рядов.

12.1 Основные понятия. Сходимость числовых рядов. Свойства сходящихся рядов.

Определение: Числовым рядом называется бесконечная последовательность чисел , соединенных знаком сложения:

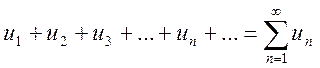,                                    (12.1)

При этом слагаемые ,называют членами этого ряда, а  — общим членом ряда. Ряд (12.1) считается заданным, если известен его общий член , выраженный как функция номера , т.е. . Например, ряд с общим членом 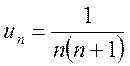. имеет вид

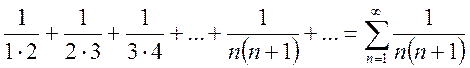.                         (12.2)

Более сложной является обратная задача: по нескольким первым членам ряда написать общий член ряда. Эта задача имеет бесконечно много решений, но иногда удается найти самое естественное решение. Например, простейшей формой общего члена ряда

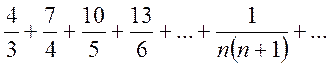 есть .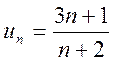

Считая, что ряд (12.1) задан, мы можем построить частичные суммы этого ряда, т.е.

;

;

;

……………………………….

.

Определение. Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, т.е.

                                               (12.3)

Число  называют суммой этого ряда и понимают, что

.

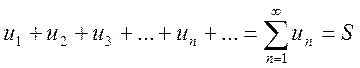Если конечного предела последовательности частичных сумм не существует, то ряд называется расходящимся.

Рассмотрим понятия сходимости и расходимости на примерах.

Пример 1. Исследовать сходимость геометрического ряда

,                     (12.4)

где .

Решение. Известно, что  — сумма  первых членов геометрической прогрессии выражается формулой

.

Здесь приходится рассматривать отдельно четыре случая.

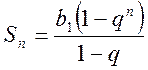1)  Пусть . Тогда  и, следовательно,

.

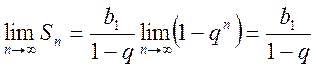В этом случае ряд (12.4) сходится и его сумма равна .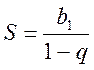

2)  Пусть . Тогда 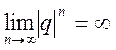 и, следовательно,  неограничено возрастает. Поэтому ряд (12.4) в этом случае расходится.

3)  Пусть . Тогда ряд (12.4) принимает такой вид

Легко видеть, что  и . Следовательно, ряд (12.4) в этом случае расходится .

4)  Пусть . В этом случае ряд (12.4) принимает вид

 .

Величина  будет равна нулю или  в зависимости от того, будет ли  четно или нечетно. Ясно, что  при  не стремится ни к какому пределу при неограниченном возрастании . Ряд (12.4) в этом случае расходится.

Вывод: геометрический ряд (12.4) сходится к сумме 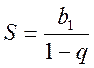 при  и расходится при .

Пример 2. Исследуем по определению сходимость ряда (12.2)

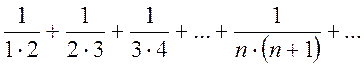                               (12.2)

Решение. Очевидно, что имеет место равенство 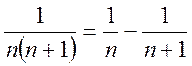. Используя его, преобразуем частичную сумму ряда

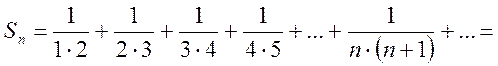
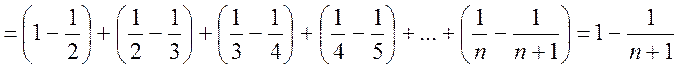
Тогда .

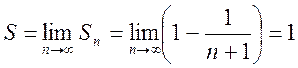Таким образом, ряд (12.1) сходится, и сумма его равна 1.

Если ряд (12.2) сходится, то разность между суммой  и частичной суммой  его

называется n-м остатком ряда. Остаток  ряда представляет собой ту погрешность, которая получится, если в качестве приближенного значения суммы ряда  взять сумму  первых n членов этого ряда.

Так как  есть предел последовательности , то

.                                     (12.6)

Поэтому, взяв достаточно большое число членов сходящегося ряда, можно сумму этого ряда вычислить с любой степенью точности.

Отсюда ясно, что первой основной задачей теории рядов является исследование сходимости ряда. Задача о нахождении суммы сходящегося ряда имеет второстепенное значение, так как, после того  как установлена сходимость ряда, сумма его в большинстве практически важных случаев приближенно легко может быть найдена.

Рассмотрим некоторые свойства сходящихся рядов.

1. Если ря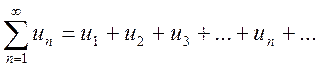д  сходится и имеет сумму S, то и ряд  (полученный умножением данного ряда на число ) тоже сходится и имеет сумму , причем

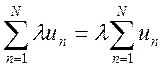                                      (12.7)

Доказательство этого свойства вытекает из перехода к пределу при  в равенстве .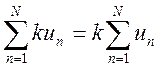

Под суммой (разностью) двух рядов 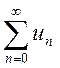 и 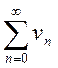 понимается соответственно ряд вида .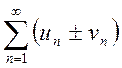

2. Если ряды 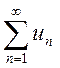 и 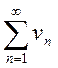 сходятся и их суммы соответственно равны  и , то и ряд 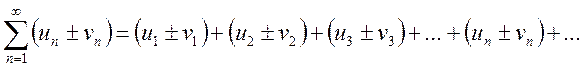 тоже сходится и его сумма равна .

Действительно, так как 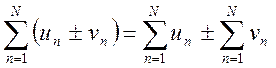 для любого конечного N, то при  в пределе получаем требуемое утверждение.

3. Если ряд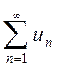 сходится, то ряд, полученный из данного путем отбрасывания (или приписывания) конечного числа членов тоже сходится.

Пусть в сходящемся ряде 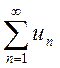 отброшены n членов (в принципе можно отбрасывать члены с любыми номерами, лишь бы их было конечное число). Покажем, что полученный ряд

,

имеющий частичную сумму , тоже сходится.

Очевидно, что . Отсюда следует, что при фиксированном n конечный предел  существует тогда и только тогда, когда существует конечный предел . А это означает, что ряд сходится.

4. Для того чтобы ряд 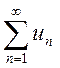 сходился, необходимо и достаточно, чтобы при  остаток ряда стремился к нулю, т.е. чтобы

.                                              (12.9)

Необходимость следует из равенства (12.6).

12.2 Необходимый признак сходимости. Гармонический ряд.

Теорема. Если ряд сходится, то предел его общего члена  при  равен нулю, т.е.

.                                              (12.9)

Доказательство. Имеем

.

.

Вычитая из верхнего равенства нижнее, получаем

.

Так как данный ряд сходится, то  и . Отсюда

,

что и требовалось доказать.