Числовые ряды. Знакопеременные ряды. Функциональные ряды. Приложение рядов, страница 6

Если  функциональный ряд (13.10) сходится в каждой точке  некоторого множества, то ряд называется сходящимся на этом множестве, а функция , определяется формулой

,

называется суммой этого ряда на данном множестве.

Степенным рядом называется функциональный ряд вида

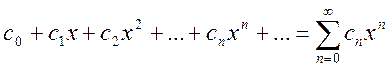                                                            (13.11),

где  – постоянные коэффициенты степенного ряда.

Иногда рассматривают степенной ряд более общего вида

,

где . Этот ряд легко приводится к виду (13.11), если положить . Поэтому дальше будем рассматривать степенные ряды вида (13,11).

Структура области сходимости степенного ряда устанавливается теоремой Абеля.

1)  Если ряд (13.11) сходится при некотором значении , то он абсолютно сходится при всех значениях , для которого .

2)  Если степенной ряд (13.11) расходится при , то он расходится для всех , для которых .

Доказательство.

1. По условию ряд (13.11) сходится при , следовательно, выполняется необходимый признак сходимости . Отсюда следует, что последовательность  ограниченна, т.е. существует такое число , что для всех  справедливо неравенство

.                                                         (13.12)

Представим ряд (13.11) в виде

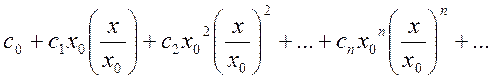
и рассмотрим ряд составленный из абсолютных членов этого ряда

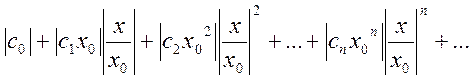                           (13.13)

Члены ряда (13.13) согласно неравенству (13.12) меньше соответствующих членов ряда

,

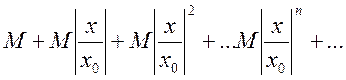представляющего геометрический ряд, сходящийся при 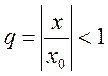, т.е . Следовательно, на основании первого признака сравнения ряд (13.11) сходится абсолютно.

2. По условию ряд (13.11) расходится при . Покажем, что он расходится для всех , удовлетворяющих условию  предположим противное , т.е. при  ряд (13.11) сходится. Тогда по доказанному выше он должен сходится и в точке  (ибо ), что противоречит условию, что в точке  ряд расходится. Следовательно, для  всех х таких, что  степенной ряд (13.11) расходится. Теорема доказана.

Из теоремы Абеля следует, что для любого степенного ряда (13.11) существует такое неотрицательное число , что при  ряд сходится, а при  расходится. Число  называется радиусом сходимости, а интервал  - интервалом сходимости степенного ряда. На концах интервала сходимости, т.е при  и , ряд может как

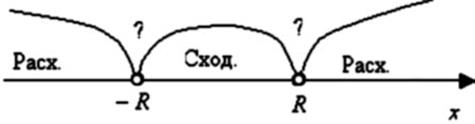
Рис. 13.1

сходиться так и расходиться.

В простейших случаях радиус сходимости степенного ряда (13.11) может быть определен, например, с помощью признака Даламбера. Для этого рассмотрим ряд, составленный из абсолютных величин его членов

                            (13.14)

в котором все коэффициенты , по крайней мере начиная с некоторого номера , отличны от нуля. По признаку Даламбера ряд (13.14) сходится, если

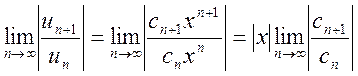
будет меньше 1, т.е.

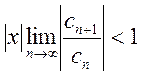 или .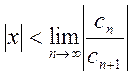

Если этот предел существует, то он и является радиусом сходимости ряда (13.11), т.е.

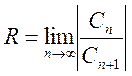                                             (13.15)

Замечание 1. Если , то интервал сходимости представляет собой всю числовую прямую. В случае, если , то степенной ряд (13.11) сходится лишь в точке , т.е интервал вырождается в точку.

Пример 3. Найти область сходимости степенного ряда .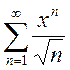

Решение. Здесь 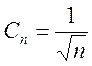, 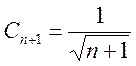. Используя формулу (13.15), находим

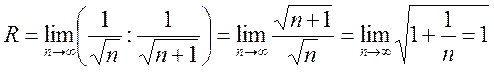
Следовательно, исследуемый ряд сходится в интервале .

Чтобы решить вопрос о сходимости ряда на концах интервала, положим сначала . Тогда исследуемый ряд имеет вид

 .

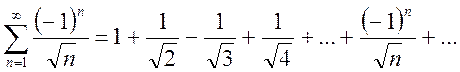Этот знакочередующийся ряд сходится в силу теоремы Лейбница. На правом конце интервала сходимости при  получаем ряд

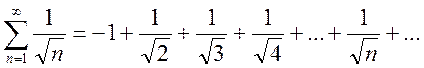
который расходится, как обобщенный гармонический ряд при 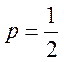. Тогда область сходимости исследуемого ряда – промежуток .

Замечание 2. Для степенного ряда

радиус сходимости вычисляется по той же формуле (13.15), но областью сходимости будет промежуток радиуса  с центром в точке  

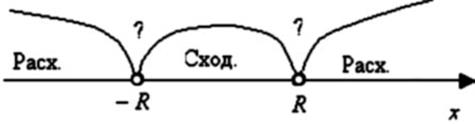
                       Рис. 13.2

Замечание 3. Другую формулу для нахождения радиуса сходимости степенного ряда можно получить из радикального признака Коши