Доказательство. Рассмотрим криволинейную
трапецию образованную графиком положительной непрерывной, монотонно убывающей
функции ![]() при
при ![]() .
.
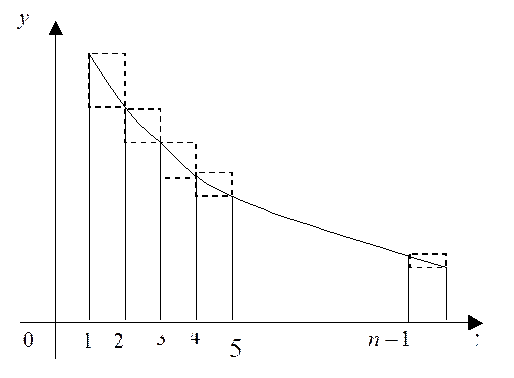 Впишем в
криволинейную трапецию и опишем около неё две ступенчатые фигуры состоящие из
прямоугольников с основаниями
Впишем в
криволинейную трапецию и опишем около неё две ступенчатые фигуры состоящие из
прямоугольников с основаниями ![]() . Высотами прямоугольников вписанной
фигуры служат
. Высотами прямоугольников вписанной
фигуры служат ![]() , а описанной
, а описанной ![]() . Известно, что
. Известно, что
площадь криволинейной трапеции выражается интегралом
Рис.12.1
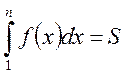 .
.
Площадь вписанной фигуры равна
![]() .
.
Площадь описанной фигуры
![]() .
.
Тогда имеет место равенство ![]() или
или ![]() .
.
Из последнего неравенства получаем оценки
![]() и
и ![]() , т.е.
, т.е.
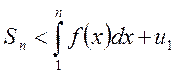 и
и 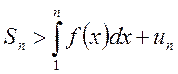 .
.
Если несобственный интеграл 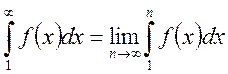 сходится и
равен
сходится и
равен ![]() , то имеет место оценка
, то имеет место оценка ![]() , т. е.
последовательность частичных сумм ограниченна сверху, поэтому существует
конечный предел
, т. е.
последовательность частичных сумм ограниченна сверху, поэтому существует
конечный предел ![]() , значит исследуемый ряд сходится.
, значит исследуемый ряд сходится.
Если несобственный интеграл 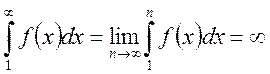 расходится, то
из оценки
расходится, то
из оценки 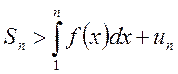 следует, что последовательность частичных сумм
неограничена, следовательно исследуемый ряд расходится. Теорема доказана.
следует, что последовательность частичных сумм
неограничена, следовательно исследуемый ряд расходится. Теорема доказана.
Пример 10.Исследовать
сходимость обобщенного гармонического ряда 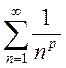 .
.
Решение. Функция 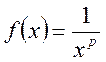 при
при ![]() знакоположительная
и монотонно убывающая
знакоположительная
и монотонно убывающая ![]() . Поэтому исследуемый ряд и несобственный интеграл
. Поэтому исследуемый ряд и несобственный интеграл 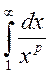 ведут себя
одинаково. Вычислим несобственный интеграл
ведут себя
одинаково. Вычислим несобственный интеграл
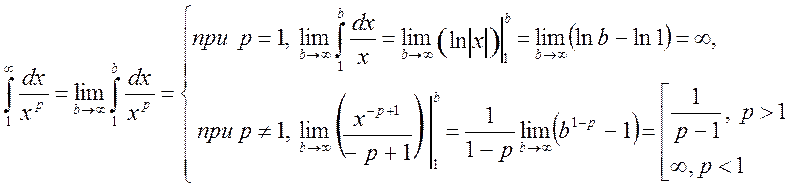 .
.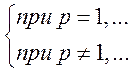
Таким образом, обобщенный гармонический
ряд сходится при ![]() и расходится при
и расходится при ![]() .
.
Пример 11.Исследовать
сходимость ряда 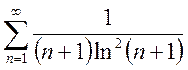 .
.
Решение. Для функции 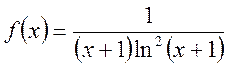 очевидно
выполняется условие интегрального признака. Поэтому вычислим несобственный
интеграл
очевидно
выполняется условие интегрального признака. Поэтому вычислим несобственный
интеграл 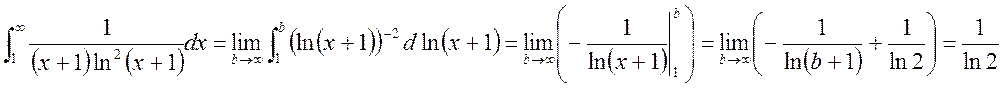 , т.е. несобственный интеграл сходится. Тогда по
интегральному признаку Коши исследуемый ряд тоже сходится.
, т.е. несобственный интеграл сходится. Тогда по
интегральному признаку Коши исследуемый ряд тоже сходится.
У П Р А Ж Н ЕН И Я .
1. Написать в простейшей форме общий член ряда:
a)
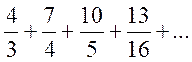 ; b)
; b) 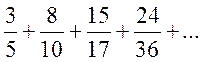 .
.
2. Найти сумму ряда, пользуясь непосредственно Определением сходимости:
a)
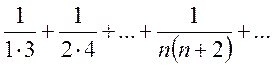 ; b)
; b) 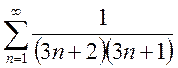 .
.
3. Исследовать сходимость ряда, применив необходимый признак сходимости:
a)
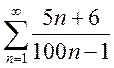 ; b)
; b) 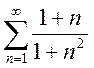 ; c)
; c) 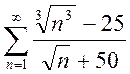 .
.
4. Исследовать сходимость с помощью теорем сравнения:
a)
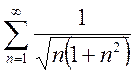 ; b)
; b) 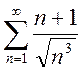 ; c)
; c) 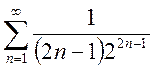 ;
;
d)
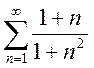 ; e)
; e) 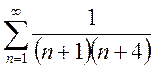 ; f)
; f)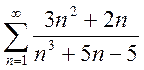 ;
;
5. Исследовать сходимость ряда с помощью признака Даламбера:
a)
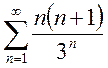 b)
b)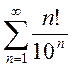 ; c)
; c)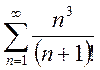 ;
;
d)
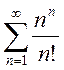 ; e)
; e)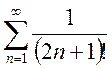 ; f)
; f)
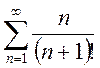 .
.
6.Исследовать сходимость с помощью признаков Коши:
a) 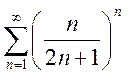 ; b)
; b) 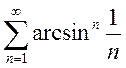 ; c)
; c)
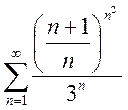 ;
;
d) 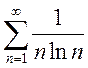 ; e)
; e) 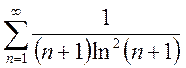 ; f)
; f) 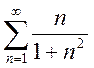 .
.
7. Исследовать сходимость ряда:
a) 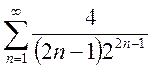 ; b)
; b) 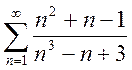 ; c)
; c) 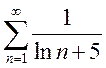 ;
;
d)
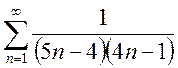 ; e)
; e) 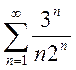 ; f)
; f) 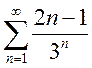 .
.
Лекция 13. Знакопеременные ряды. Функциональные ряды
13.1. Знакопеременные ряды. Абсолютная сходимость. Знакочередующиеся ряды. Признак Лейбница
Рассмотрим ряды, часть членов которых положительна, а часть отрицательна. Такие ряды называются знакопеременными.
Теорема. Если для знакоопределенного ряда
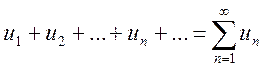 (13.1)
(13.1)
ряд, составленный из абсолютных величин его членов
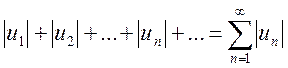 (13.2)
(13.2)
сходится, то данный ряд (13.1) также сходится.
Доказательство.Рассмотрим вспомогательный ряд
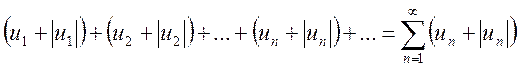 (13.3)
(13.3)
Так как ![]() и ряд
и ряд 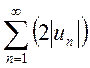 в силу
сходимости ряда (13.2) сходится, то на основании первого признака сравнения ряд
(13.3) также сходится. Тогда исследуемый ряд (13.1) можно представить в виде разности
двух сходящихся рядов
в силу
сходимости ряда (13.2) сходится, то на основании первого признака сравнения ряд
(13.3) также сходится. Тогда исследуемый ряд (13.1) можно представить в виде разности
двух сходящихся рядов
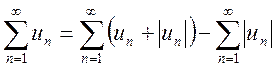
и, следовательно, он есть сходящийся (см. свойство 2 сходящихся рядов).
Замечание. Обратное утверждение неверно, т.е. если данный ряд сходится, то ряд, составленный из модулей его членов, может как сходится так и расходится.
Определение. Ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов.
Ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин, расходится.
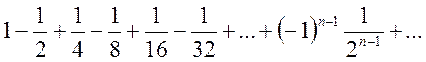 (13.4)
(13.4)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.