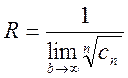 (13.6)
(13.6)
Пример 4. Найти область сходимости степенного ряда
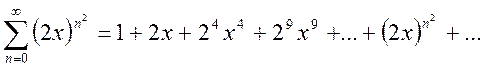
Решение.
Вычислить радиус сходимости по формулам (13.15) или (13.16) не представляется
возможным, так как в этом ряде коэффициенты ![]() равны
нулю. Поэтому непосредственно применим признак Даламбера, полагая
равны
нулю. Поэтому непосредственно применим признак Даламбера, полагая 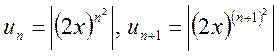 .
.

Следовательно, ряд сходится при 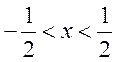 или на интервале
или на интервале 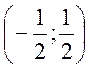 .
.
Исследуем сходимость
на концах интервала сходимости: при 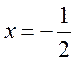 ряд
принимает вид
ряд
принимает вид 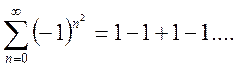 , а при
, а при 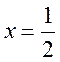 вид
вид  т.е оба ряда расходятся, так как
не выполняется необходимый признак сходимости. Итак, область сходимости ряда
т.е оба ряда расходятся, так как
не выполняется необходимый признак сходимости. Итак, область сходимости ряда 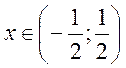 .
.
Свойства степенных рядов. В курсах математического анализа доказывается, что степенной ряд в своем интервале сходимости по отношению к операциям дифференцирования и интегрирования ведет себя также, как многочлен с конечным числом членов.
Теорема 1. Если степенной ряд
![]() (13.17)
(13.17)
имеет
интервал сходимости ![]() , то ряд полученный дифференцированием ряда (13.17)
, то ряд полученный дифференцированием ряда (13.17)
![]() (13.18)
(13.18)
будет
иметь тот же интервал сходимости ![]() , причем его сумма
, причем его сумма ![]() .
.
Теорема 2. Степенной ряд (13.17) можно
почленно интегрировать на любом отрезке ![]() , целиком принадлежащем интервалу
сходимости
, целиком принадлежащем интервалу
сходимости ![]() , т.е.
, т.е.
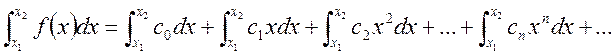 . (13.19)
. (13.19)
У п р а ж н е н и я.
1. Исследовать сходимость ряда с помощью признака Лейбница:
a.
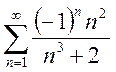 ; b.
; b. 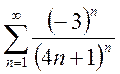 ; c.
; c. 
2.
Вычислить
с точностью до ![]() сумму ряда:
сумму ряда:
a.
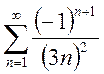 ; b.
; b. 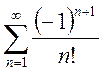 ; c.
; c. 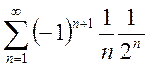
3. Установить какие из данных рядов сходятся абсолютно, какие условно, какие расходятся:
a.
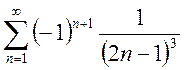 ; b.
; b.  ; c.
; c. 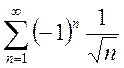 ;
;
d.  ; e.
; e. 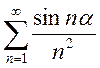 ; f.
; f.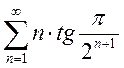 .
.
4. Найти область сходимости степенных рядов:
a.
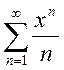 ; b.
; b.  ; c.
; c. 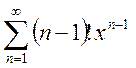 ;
;
d.  ; e.
; e. 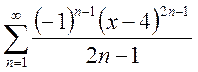 ; f.
; f.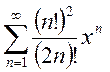 .
.
Лекция 14. Функциональные ряды. Приложение рядов.
14.1. Ряды Тейлора и Макларена. Разложение основных элементарных функций в ряд
Предположим, что функция f(x), определенная и n раз дифференцируемая
в окрестности точки ![]() , может быть представлена в виде суммы степенного ряда
, может быть представлена в виде суммы степенного ряда
![]() ,
(14.1)
,
(14.1)
сходящегося в интервале (![]() ). В этом случае
говорят, что функция f(x)
раскладывается в степенной ряд в окрестности
точки
). В этом случае
говорят, что функция f(x)
раскладывается в степенной ряд в окрестности
точки ![]() по степеням
по степеням ![]() . Найдем
коэффициенты разложения
. Найдем
коэффициенты разложения ![]() этого ряда. Для этого найдем производные функции f(x), дифференцируя
степенной ряд (14.1) n раз
этого ряда. Для этого найдем производные функции f(x), дифференцируя
степенной ряд (14.1) n раз

![]() .
.
Из этих равенств получаем
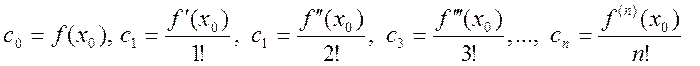 .
.
Подставляя значения коэффициентов ![]() в (14.1) получим
ряд
в (14.1) получим
ряд
 (14.2)
(14.2)
который называют рядом Тейлора для функции f(x).
При ![]() получаем ряд Макларена
получаем ряд Макларена
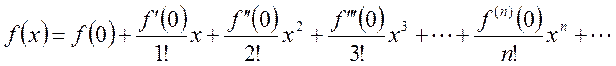 . (14.3)
. (14.3)
Обратная
задача: пусть дана бесконечно
дифференцируемая функция f(x). Составим для нее формально ряд Тейлора в окрестности
точки ![]() :
:
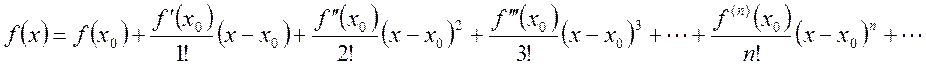 .
.
Поставим вопрос: будет ли сумма данного ряда Тейлора S(x) совпадать с функцией f(x), для которой он построен. Оказывается не всегда. На этот вопрос дает ответ теорема:
Теорема.
Для того чтобы бесконечно дифференцируемая в точке ![]() функция f(x)
являлась суммой составленного ля нее ряда Тейлора, необходимо и достаточно,
чтобы остаточный член ряда
функция f(x)
являлась суммой составленного ля нее ряда Тейлора, необходимо и достаточно,
чтобы остаточный член ряда
![]() (14.4)
(14.4)
стремился
к нулю при ![]() .
.
Доказательство (необходимость): если
функция f(x)
есть сумма ряда Тейлора, то ![]() .
.
Пусть f(x) есть сумма ряда Тейлора, т.е. ![]() . Тогда из (14.4)
следует
. Тогда из (14.4)
следует ![]()
![]() ч.т.п. .
ч.т.п. .
(Достаточность): если ![]() , то функция f(x)
является суммой ряда Тейлора.
, то функция f(x)
является суммой ряда Тейлора.
Пусть ![]() . Тогда из (14.4) следует, что
. Тогда из (14.4) следует, что
![]() .
.
А это и значит, что f(x) есть сумма ряда, ч.т.д.
Вывод:
эта теорема показывает, что для исследования вопроса о
разложимости функции в ряд Тейлора нужно исследовать поведение его остаточного
члена при ![]() .
.
Можно доказать, что если функция f(x) разложима в ряд
Тейлора в окрестности т.![]() , то это разложение единственное.
, то это разложение единственное.
Если остаточный член ![]() представить в
форме Лагранжа
представить в
форме Лагранжа
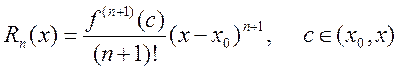 , (14.5)
, (14.5)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.