2) гармонический
ряд 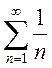 — расходится;
— расходится;
3) обобщенный гармонический ряд
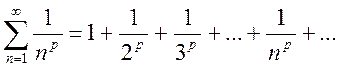 (12.12)
(12.12)
сходится при ![]() , расходится при
, расходится при ![]() 1 (доказательство см. в пр. 10).
1 (доказательство см. в пр. 10).
2. Второй признак сравнения.
Теорема. Пусть даны два знакопостоянных
ряда 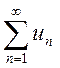 и
и 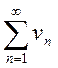 и существует конечный предел отношения
их общих членов
и существует конечный предел отношения
их общих членов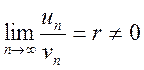 , тогда рассматриваемые ряды одновременно сходятся
или расходятся.
, тогда рассматриваемые ряды одновременно сходятся
или расходятся.
Доказательство. Так как 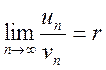 ,
то по определению предела числовой последовательности для любого
,
то по определению предела числовой последовательности для любого ![]() существует такой номер
существует такой номер ![]() , начиная с которого для всех
, начиная с которого для всех ![]() выполняется неравенство
выполняется неравенство 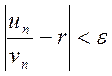 , или
, или 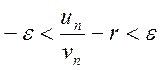 , или
, или ![]() , или
, или ![]() .
.
Если ряд 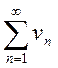 сходится, то сходится ряд
сходится, то сходится ряд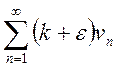 и в силу первого признака
сравнения будет сходится ряд
и в силу первого признака
сравнения будет сходится ряд 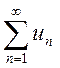 . Аналогично,
если сходится ряд
. Аналогично,
если сходится ряд 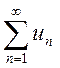 , то сходится ряд
, то сходится ряд 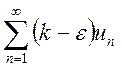 и сходится ряд
и сходится ряд 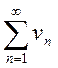 . Таким образом, из сходимости
одного ряда следует сходимость другого. Утверждение о расходимости рядов
доказывается аналогично.
. Таким образом, из сходимости
одного ряда следует сходимость другого. Утверждение о расходимости рядов
доказывается аналогично.
Пример
7. Исследовать сходимость ряда 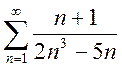 .
.
Решение.
В качестве ряда для сравнения выбираем сходящийся ряд 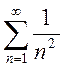 (выбор такого ряда для сравнения определяется
тем, что при больших
(выбор такого ряда для сравнения определяется
тем, что при больших ![]() многочлен эквивалентен старшему
члену и
многочлен эквивалентен старшему
члену и 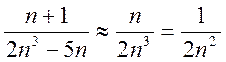 ). Так как
). Так как 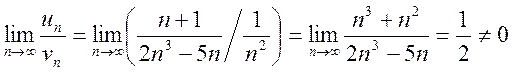 , то исследуемый ряд, как и
сравниваемый ряд, сходится.
, то исследуемый ряд, как и
сравниваемый ряд, сходится.
3. Признак Даламбера.
Теорема. Пусть для знакоположительного
ряда 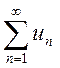 существует
существует 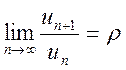 . Тогда, если
. Тогда, если![]() , то ряд
сходится; если
, то ряд
сходится; если ![]() , то ряд расходится;
, то ряд расходится;
Доказательство. Из определения предела последовательности
следует, что для любого ![]() существует такой номер
существует такой номер ![]() , что для всех
, что для всех ![]() выполняется неравенство
выполняется неравенство 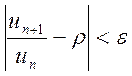 или
или 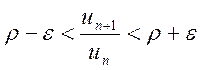 .
.
1)
Пусть
![]() . Выбираем
. Выбираем![]() настолько малым, чтобы число
настолько малым, чтобы число ![]() , т.е.
, т.е.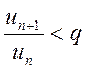 или
или ![]() .Последнее
неравенство будет выполнятся для всех
.Последнее
неравенство будет выполнятся для всех ![]() , т.е. для
, т.е. для ![]() ,
, ![]() , …, т.е.
, …, т.е.
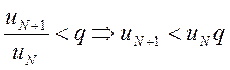 ,
,
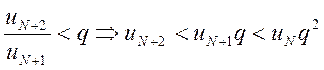 ,
,
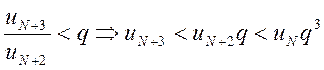 ,
,
………………………………………..
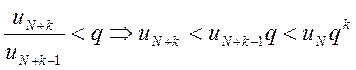 .
.
Из этих оценок следует, что члены ряда ![]() меньше соответствующих членов
геометрического ряда
меньше соответствующих членов
геометрического ряда ![]() , сходящегося при
, сходящегося при ![]() . Тогда на основании первого
признака сравнения ряд
. Тогда на основании первого
признака сравнения ряд ![]() тоже сходится, а значит сходится
и рассматриваемый ряд
тоже сходится, а значит сходится
и рассматриваемый ряд 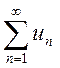 , отличающийся от предыдущего на
первые
, отличающийся от предыдущего на
первые ![]() членов.
членов.
2) Пусть ![]() . Выберем
. Выберем ![]() настолько малым, чтобы
настолько малым, чтобы ![]() . Тогда из условия
. Тогда из условия 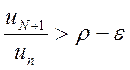 следует, что
следует, что 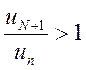 , а это значит, что члены ряда
возрастают, начиная с номера
, а это значит, что члены ряда
возрастают, начиная с номера ![]() , поэтому
, поэтому ![]() , т.е. не выполнено необходимое
условие сходимости, и ряд расходится.
, т.е. не выполнено необходимое
условие сходимости, и ряд расходится.
а)
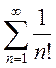 , б)
, б) 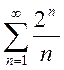 .
.
Решение.
а) Так как ![]() и
и 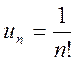 ,
,
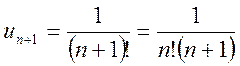 , то по признаку Даламбера
, то по признаку Даламбера 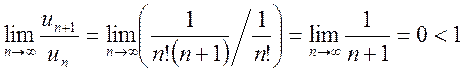 ряд сходится (
ряд сходится (![]() ) .
) .
б) Так как 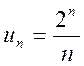 и
и ![]()
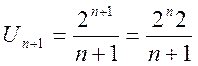 , то по признаку Даламбера
, то по признаку Даламбера 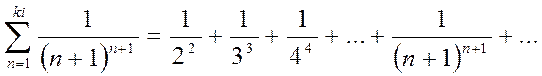 ряд расходится.
ряд расходится.
Замечание 1.
Если 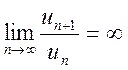 , то ряд расходится.
, то ряд расходится.
Замечание 2. Если 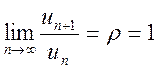 , то признак Даламбера не дает
ответа на вопрос сходимости ряда и рекомендуется воспользоваться другим
признаком сходимости.
, то признак Даламбера не дает
ответа на вопрос сходимости ряда и рекомендуется воспользоваться другим
признаком сходимости.
Радикальный признак Коши.
Теорема. Если для знакоположительного
ряда 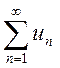
![]() , то при
, то при ![]() ряд сходится, при
ряд сходится, при ![]() расходится.
расходится.
Доказательство. Из определения предела последовательности
следует, что для любого ![]() существует такой номер
существует такой номер ![]() , что для всех
, что для всех ![]() выполняется неравенство
выполняется неравенство ![]() , или
, или ![]() .
.
1)
Пусть
![]() . Выберем
. Выберем ![]() достаточно малым, чтобы
достаточно малым, чтобы ![]() . Тогда для всех
. Тогда для всех
![]() , т.е. для
, т.е. для![]() будет справедливо неравенство
будет справедливо неравенство
![]()
По первой теореме
сравнения, из сходимости геометрического ряда 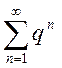 при
при
![]() , следует сходимость исследуемого
ряда
, следует сходимость исследуемого
ряда 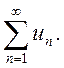
2)
Пусть
![]() . Выберем
. Выберем ![]() достаточно малым, чтобы
достаточно малым, чтобы ![]() . Используем
неравенство
. Используем
неравенство ![]() или
или ![]() , которое справедливо при всех
, которое справедливо при всех ![]() . Тогда имеем
оценку
. Тогда имеем
оценку ![]() общих членов двух рядов
общих членов двух рядов 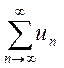 и
и 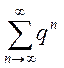 . Так как
геометрический ряд
. Так как
геометрический ряд 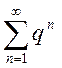 при
при ![]() расходящийся, то по первой
теореме сравнения исследуемый ряд тоже расходится.
расходящийся, то по первой
теореме сравнения исследуемый ряд тоже расходится.
Пример 9. Исследовать
сходимость ряда 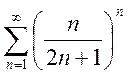 .
.
Решение. Так как 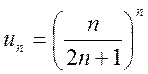 , то
, то 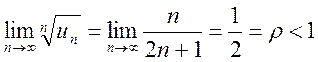 , то по
радикальному признаку Коши ряд сходится.
, то по
радикальному признаку Коши ряд сходится.
Замечание: При ![]() признак Коши не
дает ответа на вопрос сходимости расходимости ряда и необходимо применять
другой признак сходимости.
признак Коши не
дает ответа на вопрос сходимости расходимости ряда и необходимо применять
другой признак сходимости.
Интегральный признак Коши.
Теорема. Пусть
члены знакоположительного ряда 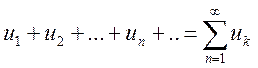 являются
значениями при
являются
значениями при ![]() некоторой положительной непрерывной,
монотонно убывающей на
некоторой положительной непрерывной,
монотонно убывающей на ![]() функции
функции ![]() , причем
, причем
![]() .
.
Тогда несобственный интеграл 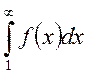 и исследуемый
ряд
и исследуемый
ряд 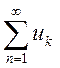 одновременно сходятся или расходятся
(ведут себя одинаково).
одновременно сходятся или расходятся
(ведут себя одинаково).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.