Элементы теории определителей. Матрицы и действия над ними. Элементарные операции над матрицами. Векторное произведение и его свойства

Лекция № 1.

Элементы теории определителей.

Определение 1. Система элементов, записанных в определенном порядке, называется матрицей этих элементов.

 ;

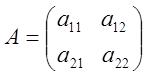Определение 2. Определителем второго порядка, соответствующим матрице А, называется число  .

Обозначение: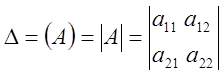   

Свойства. 1) Определитель не измениться, если его строки поменять местами с соответствующими столбцами.

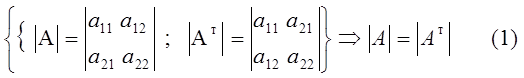
Примечание. Операция замены строк столбцами и наоборот, называется операцией транспонирования.

Следствие  1) Все Свойства, сформулированные для строк определителя, справедливы

 в той же формулировке и для столбцов.

2) При перестановке двух строк определитель изменит знак на противоположный, сохраняя абсолютную величину. 

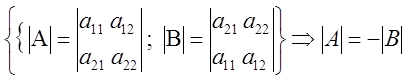                            (2)

3) Определитель с двумя одинаковыми строками равен нулю.

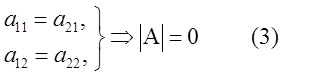
Доказательство: 

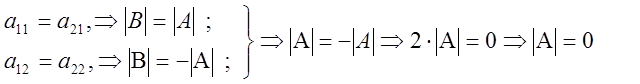
4) Общий множитель всех элементов строки можно выносить за знак определителя.

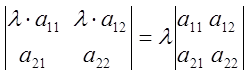                                                 (4)

5) Определитель с нулевой строкой равен нулю.

   

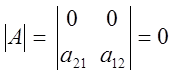
6)        

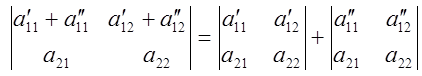
Доказательство :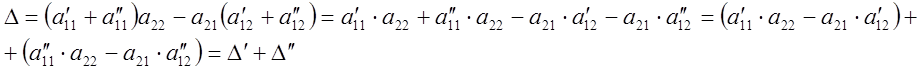

7) Если к элементам какой либо строки определителя прибавить соответствующие элементы другой строки, умноженное на одно и то же число, то определитель не изменит своей величины.

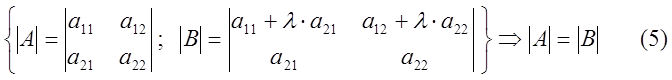
Доказательство.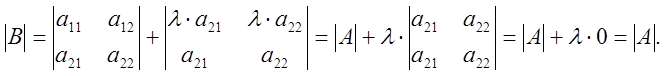 

Определители 3-го порядка.

Определение Минором М_ij элемента а_ij определителя называется определитель, который получается из исходного путем вычеркивания тех строки и столбца, на пересечении которых расположен элемент а_ij .

Определение Алгебраическим дополнением А_ij элемента а_ij определителя называют минор

М_ij этого элемента, взятый со знаком “+”, если сумма номеров строки и столбца элемента а_ij –четная, и со знаком “-“ - в противном случае, т.е.

А_ij = М_ij  (7)

Определение Определителем 3-го порядка называют число, равное сумме парных произведений элементов первой строки на их алгебраические дополнения.

 

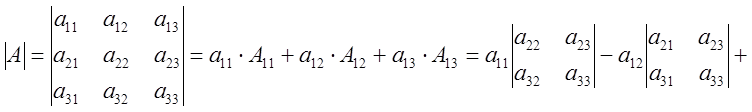
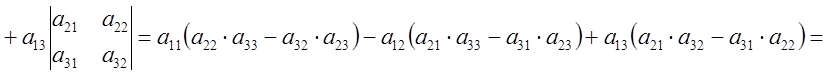
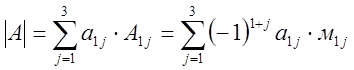                                     (8)

разложение определителя по элементам 1-й  строки

Лекция № 2.

Свойства.  Все Свойства определителей 2-го порядка остаются справедливыми и для определителей 3-го порядка.

Методы вычислений:  а) Метод треугольников; б) метод параллельных прямых.

Теорема. Значение определителя не зависит от того, по какой строке (или столбцу) он разложен.

Доказательство.

 

Следствие   

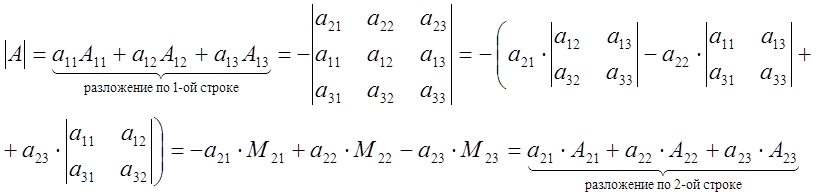
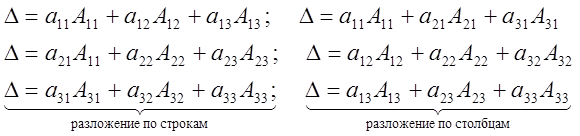
Теорема.  Сумма произведений элементов какой либо строки определителя на алгебраические дополнения соответствующего элементов другой строки равен нулю.

Например:  

Доказательство.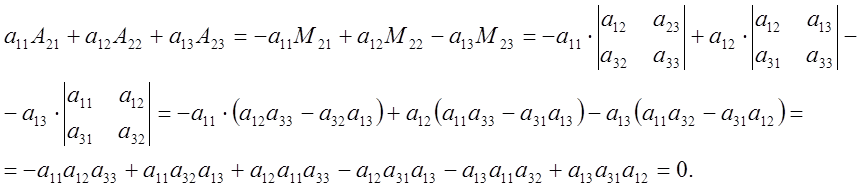

Рациональный метод. Разложение определителя по какой-либо строке (столбцу) с предварительным ее обнулением.

Пример

       

 

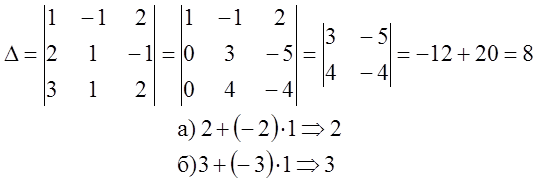
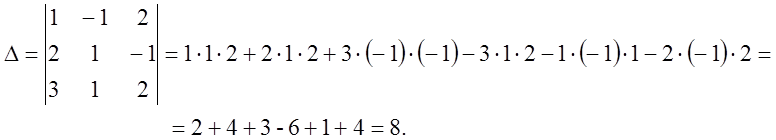
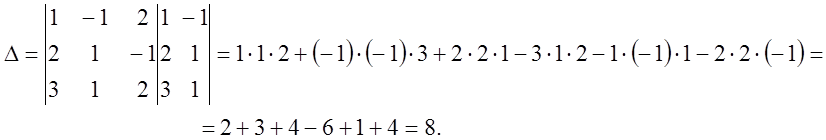
Примечание. 1.Определители n-го порядка определяется аналогично как сумма парных

элементов первой строки на их алгебраическое дополнение.

2.Все Свойства остаются в силе.

3.Основной метод: разложение с предварительным обнулением.

Пример 1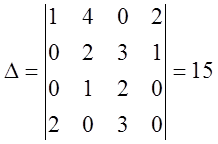 

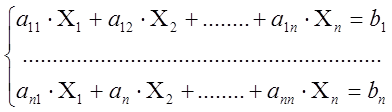Системы n линейных уравнений с n неизвестными.

    (1)   

 Определение Система вида (1) называется системой n линейных уравнений относительно n неизвестных.

неизвестные;     коэффициенты.

Определение Матрица А, составленная из коэффициентов системы (1), называется матрицей  системы, а соответствующий ей определитель главным определителем системы.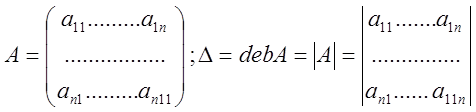

Определение Вспомогательным определителем, соответствующим переменной , называется определитель , который получается из главного определителя путем замены его i-го столбца столбцом свободных членов   

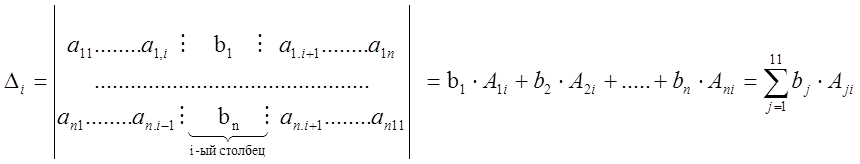
Определение Решением системы (1) называют систему чисел при подстановке которых в систему (1) вместо переменных последняя обращается в  систему верных тождеств.

Определение Система(1), имеющая по крайней мере одно решение, называется совместной.  Система не имеющая решений, называется несовместной.

Определение Система(1) называется определенной, если она имеет только одно решение, и неопределенной, если существует более одного решения.

Теорема. Для того, чтобы система(1) была определенной (т.е.имела только одно решение), необходимо и достаточно, чтобы ее главный определитель был отличен от нуля.

 

Доказательство. Для упрощения выкладок, Доказательство. проведем на примере системы 3-го порядка.

(3)

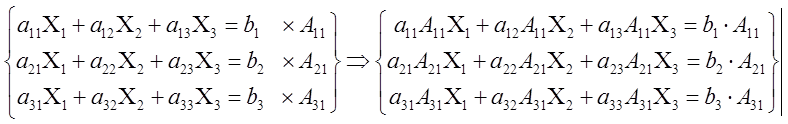
После сложения и группировки имеем

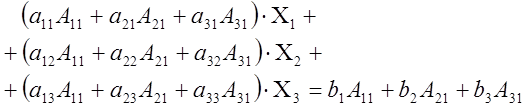
По доказанному выше: 

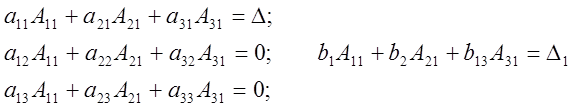
Т.Е.    Аналогично получают соотношения

Если , то деля на , получим

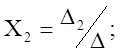
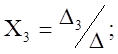                                (4)       Правило Крамера.

Т.е. система имеет единственное решение, определенное ф-ми. (4).

Следствие. Если главный определитель системы равен нулю, а хотя бы один из вспомогательных определителей не равен нулю, то система будет несовместной. Если же и главный определитель и все вспомогательные определители равны нулю, то система (1) будет либо несовместной, либо неопределенной.

Пример  (1)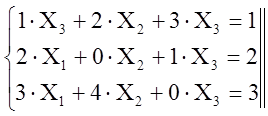      

       

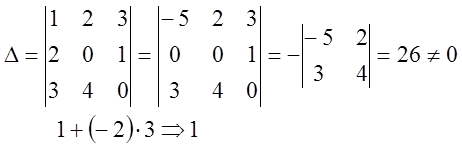
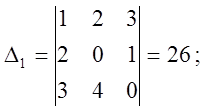
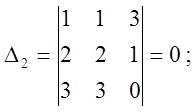
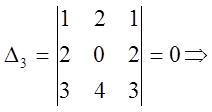
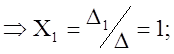
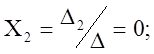
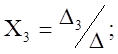                        отв.(1; 0; 0;) 

(2)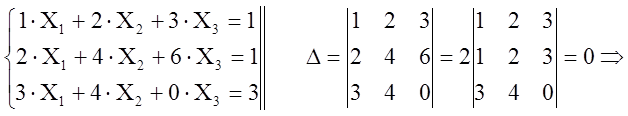система не может иметь                    одно решение.

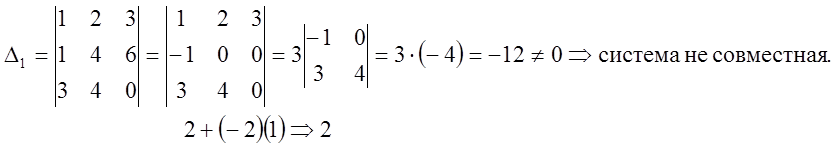
(3)      

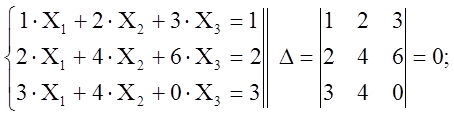
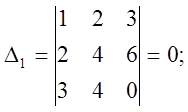
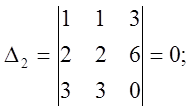
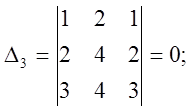
Вывод: система либо несовместная, либо неопределенная.

Примечание. Если в системе (1) все определители n-го порядка (основные и вспомогательные) равны нулю, то в этой системе хотя бы одно из уравнений есть следствие остальных.(т.е. лишние, которые можно убрать).