То есть задача о приведении квадратной формы F(![]() ) к каноническому виду
) к каноническому виду ![]() сводится к задаче о приведении к
диагональному виду матрицы линейного преобразования.
сводится к задаче о приведении к
диагональному виду матрицы линейного преобразования.
План действий по приведению формы F(![]() ) к каноническому виду:
) к каноническому виду:
1)
Составим характеристическое
уравнение матрицы А: 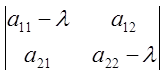 =0 и найдем и его корни
=0 и найдем и его корни ![]() и
и ![]() .
.
2)
Находим два собственных единичных
взаимно перпендикулярных ![]() и
и ![]() .
.
3)
Перейдем к новому базису ![]() . В этом базисе А=
. В этом базисе А=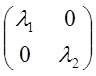 и форма имеет вид:
и форма имеет вид: ![]() =
=![]()
4) При переходе к новому базису координаты всех векторов преобразуются по формулам:
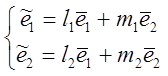 =>
=> 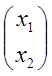 =L
=L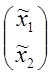 или
или ![]() =L
=L![]() где L=
где L=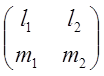 , Lт=
, Lт=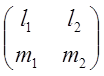 .
.
Привести к каноническому виду квадратичную формулу F![]() =
=![]() F
F![]() =
=![]() А=
А=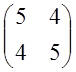 .
.
1) Составим каноническое уравнение и найдем собственные
векторы матрицы А. (уже нормированные) 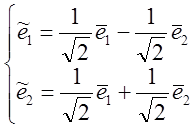 =>
=> 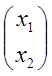 =L
=L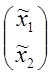 , L=
, L=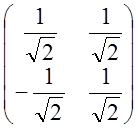 При переходе к новому базису координаты всех векторов
преобразуются по формулам:
При переходе к новому базису координаты всех векторов
преобразуются по формулам: 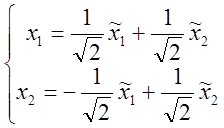 ;
;
2)
![]() =L-1AL= L-тAL;
=L-1AL= L-тAL; ![]() =
=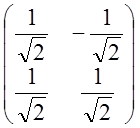

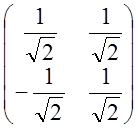 =
=![]()
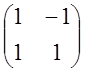

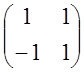 = =
= =![]()
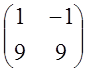
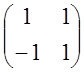 =
=![]()
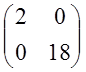 =
=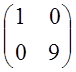 .
.
![]()
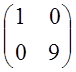
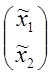 =
=
=
=![]()
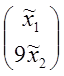 =
=![]()
Конец линейных преобразований.
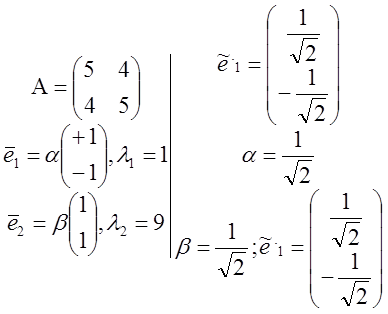
![]() ;
; ![]() =
=![]() ;
; ![]() =
=![]() .
.
Выбор нового базиса ![]() =
=![]() .
. 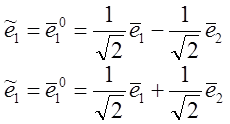 => L-1
=> L-1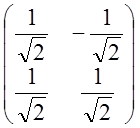 => => L=
=> => L=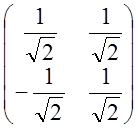
![]() =L-1AL deb L=
=L-1AL deb L=![]() +
+![]() =1
=1 ![]() =L
=L![]() L-1
L-1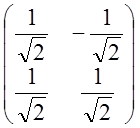 =L-т L-1=L-т
=L-т L-1=L-т
![]() =
=![]()
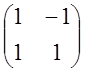

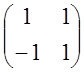
![]() =
=![]()
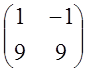
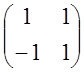 =
=![]()
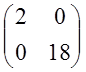 =
=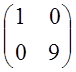 .
.
Привести к каноническому виду общее уравнение 2-го порядка
5Х2+8ХУ+5У2-18Х-18У+9=0
Решение 1) Квадратная форма имеет вид: F(х1у)=5х2+8ху+5у2
=> аn=5; а12=а21=L;а22=5; А= . Составим характеристическое уравнение:
. Составим характеристическое уравнение:
![]() =0
=0 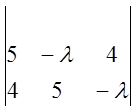 =0; (5-
=0; (5-![]() )2-42=0;
(5-
)2-42=0;
(5-![]() -4)(5-
-4)(5-![]() +4)=0
+4)=0
(9-![]() )(1-
)(1-![]() )=0 =>
)=0 => ![]() 1=9;
1=9; ![]() 2=1.
2=1.
Следовательно, в новой системе координат квадратичная форма запишется в виде
F![]() =
=![]() 1
1![]() +
+![]() 2
2![]() =9
=9![]() +1
+1![]()
2). Найдем матрицу L перехода от старой системы координат к новой. Для этого
находим собственные векторы ![]() и
и ![]() ,
соответствующие собственным числам
,
соответствующие собственным числам
![]() 1 и
1 и ![]() 2.
2.
а) ![]() 1=9,
1=9, ![]() =
=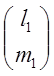 ;
; 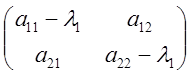
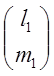 =
=![]() ;
;
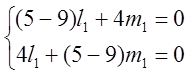
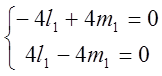
![]()
Пусть ![]() =>
=> ![]() =
=![]() =
=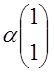 ; Выбираем
; Выбираем ![]() из
условия
из
условия 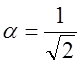
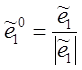
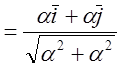
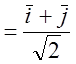
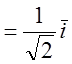
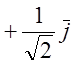
б) ![]() 2=1,
2=1, ![]() =
=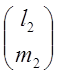 ;
; 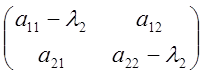
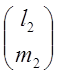 =
=![]() ;
;
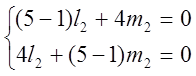
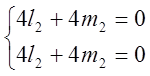
![]()
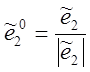
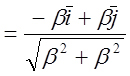
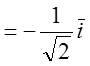
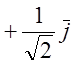
Окончательно имеем : 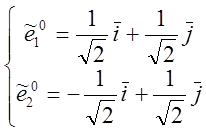 => Lт
=> Lт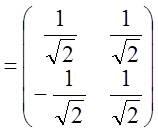 L
L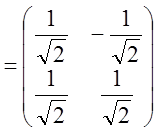 ;
; ![]() L
L![]() ;
; ![]()
![]() L
L![]() ;
; ![]()
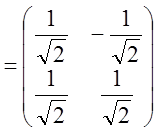
![]()
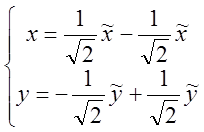
3). Найдем теперь, какой вид в новой системе координат примут младшие члены
общего уравнения в ![]() .
.
-18![]() -18
-18![]() +9=-18
+9=-18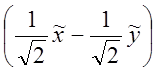 -18
-18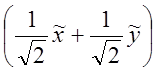 +9=
+9=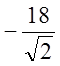
![]() +9= =
+9= =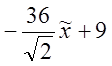
Таким образом в новой системе координат уравнение в виде:
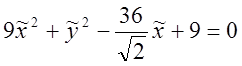 ;
; 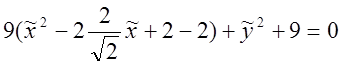
![]() ;
; 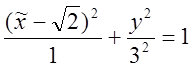
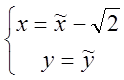
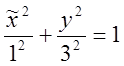
Определение: производной n-го
порядка от функции ![]() называется производная от
производной
называется производная от
производной ![]() порядка.
порядка.
![]() (1)
(1)
Пример
1. ![]() ;
; ![]() ;
; ![]() ; …
; … ![]()
Пример
2. ![]() ;
; 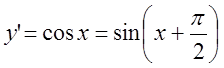 ;
; 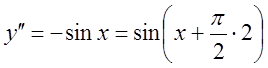 ;
; 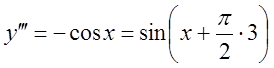 ; …
; … 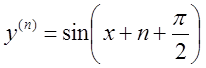
Формула Лейбница (дает возможность вычислять производную любого порядка от произведения 2 функций, минуя последовательное дифференцирование).
![]()
Например:
найти производную n-го порядка от функции ![]() .
. ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
. ![]() .
.
Ответ:
![]() .
.
Определение: Кривая рассматривается как геометрическое место последовательных положений движущейся на плоскости точки М (x, y), а координаты x и y этой точки выражаются в виде непрерывных функций параметра t (чаще всего времени).
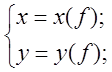
![]()
Например:
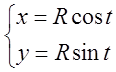 ;
; ![]() - окружность;
- окружность;
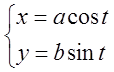 ;
; ![]() - эллипс;
- эллипс;
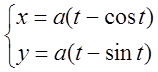 ;
; ![]() - циклоида.
- циклоида.
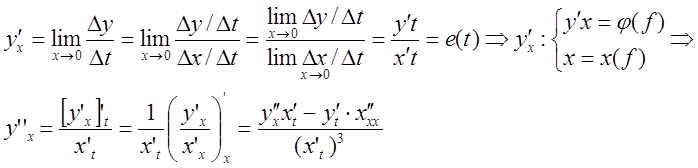
Имеем: 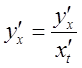 ;
; 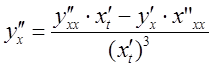
Пример: ![]() ;
; ![]() ;
; 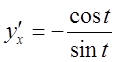 ;
; 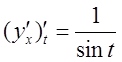 ;
; 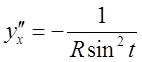 .
.
------------------------------ разрыв страницы à середина страницы 29 -------------
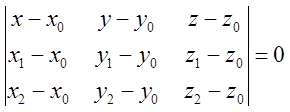 - уравнение
плоскости, проходящей через три точки.
- уравнение
плоскости, проходящей через три точки.
Угол между плоскостями.
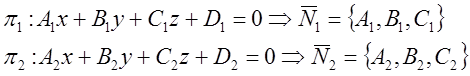
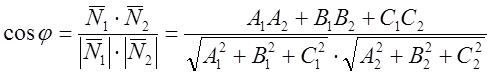
А) ![]()
![]() - условие перпендикулярности двух плоскостей.
- условие перпендикулярности двух плоскостей.
Б) ![]()
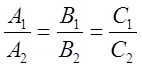 - условие
параллельности двух плоскостей.
- условие
параллельности двух плоскостей.
Определение: производной n-го
порядка от функции ![]() называется производная от
производной
называется производная от
производной ![]() порядка.
порядка.
![]() (1)
(1)
Пример
1. ![]() ;
; ![]() ;
; ![]() ; …
; … ![]()
Пример
2. ![]() ;
; 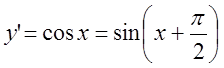 ;
; 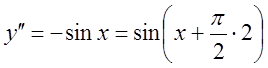 ;
; 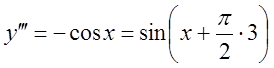 ; …
; … 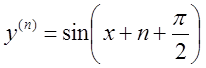
Формула Лейбница (дает возможность вычислять производную любого порядка от произведения 2 функций, минуя последовательное дифференцирование).
![]()
Например:
найти производную n-го порядка от функции ![]() .
. ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
. ![]() .
.
Ответ:
![]() .
.
Определение: Кривая рассматривается как геометрическое место последовательных положений движущейся на плоскости точки М (x, y), а координаты x и y этой точки выражаются в виде непрерывных функций параметра t (чаще всего времени).
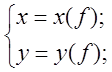
![]()
Например:
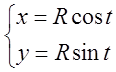 ;
; ![]() - окружность;
- окружность;
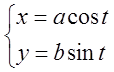 ;
; ![]() - эллипс;
- эллипс;
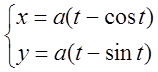 ;
; ![]() - циклоида.
- циклоида.
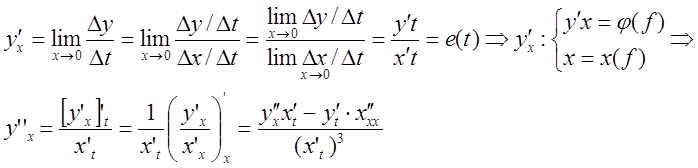
Имеем: 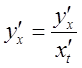 ;
; 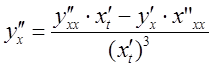
Пример: ![]() ;
; ![]() ;
; 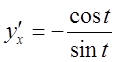 ;
; 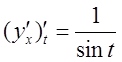 ;
; 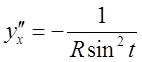 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.