![]() .
.
Пример 1. ![]() ;
; ![]()
![]() ;
Пусть х=1
;
Пусть х=1 ![]() .
. 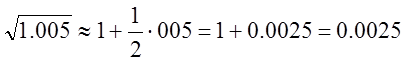
Пример 2. ![]() ;
; ![]()
![]()
![]() ; Пусть х=0
; Пусть х=0 ![]() .
.
Пример 3. 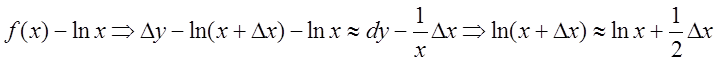 ;
Пусть х=1
;
Пусть х=1 ![]() .
.
Пример 4. ![]()
Окончательно: ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Теорема Ферма. Пусть
функция ![]() , определенная на интервале
, определенная на интервале ![]() , принимает в некоторой точке этого
интервала
, принимает в некоторой точке этого
интервала ![]() , значительно большее М или наименьшее
, значительно большее М или наименьшее ![]() свое значение. Тогда, если в точке
свое значение. Тогда, если в точке ![]() функция
функция ![]() -
дифференцируемая, то
-
дифференцируемая, то ![]() .
.
Доказательство:
1. ![]() ;
;
![]() -наибольшее значение.
-наибольшее значение. ![]() - существует,
- существует, ![]() .
.
2. Пусть ![]() , тогда
, тогда 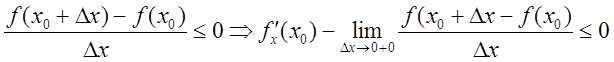
3. Пусть ![]() , тогда
, тогда 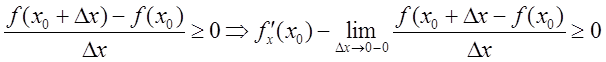
4. ![]() -существует
-существует 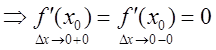 , что и требовалось доказать.
, что и требовалось доказать.
Теорема Ролля. Пусть
функция ![]() - определена и непрерывна на замкнутом
отрезке
- определена и непрерывна на замкнутом
отрезке ![]() и дифференцируема внутри этого сегмента,
т. е. на
и дифференцируема внутри этого сегмента,
т. е. на ![]() . Если на концах сегмента функция
обращается в ноль, то существует по крайней мере одна точка с этого сегмента, в
которой производная
. Если на концах сегмента функция
обращается в ноль, то существует по крайней мере одна точка с этого сегмента, в
которой производная ![]() равен нулю, т. е.
равен нулю, т. е.
![]() (1)
(1)
Другими словами, между двумя смежными корнями функции существует по крайней мере один корень производной.
Доказательство:
1. т. к. ![]() - непрерывна на замкнутом отрезке
- непрерывна на замкнутом отрезке ![]() , то она обязательно достигает своего
наибольшего М и наименьшего
, то она обязательно достигает своего
наибольшего М и наименьшего ![]() значения.
значения.
2. Если ![]() для всех
для всех ![]() .
.
3. Если ![]() , то одно из чисел, например
, то одно из чисел, например ![]() точка с, где
точка с, где ![]() ,
обязательно должна быть внутренней, т. е.
,
обязательно должна быть внутренней, т. е. ![]() (по
теореме Ферма):
(по
теореме Ферма): ![]() .
.
Примечание:
Теорема остается верной и в том случае, когда ![]() .
.
Теорема Лагранжа. Пусть
функция ![]() определена и непрерывна на замкнутом
участке
определена и непрерывна на замкнутом
участке ![]() и дифференцирована внутри его, т. е. на
часть
и дифференцирована внутри его, т. е. на
часть ![]() . Тогда существует по крайней мере одна
точка
. Тогда существует по крайней мере одна
точка ![]() , в которой функция выполняла бы условия
, в которой функция выполняла бы условия 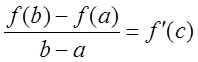 .
.
Доказательство:
1) Уравнение прямой
![]() проходит через 2 точки
проходит через 2 точки ![]() и
и ![]() .
. 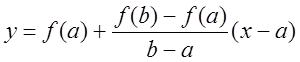 .
.
2) Рассмотрим
вспомогательную функцию 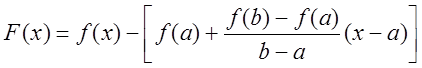 .
.
a) ![]() - определена и непрерывна на отрезке
- определена и непрерывна на отрезке ![]()
b) ![]() - дифференцируема на отрезке
- дифференцируема на отрезке ![]() , т. к. на отрезке
, т. к. на отрезке ![]() существует
существует
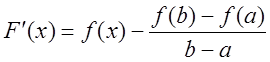 .
.
c) ![]()
![]() по
теореме Ролля
по
теореме Ролля ![]()
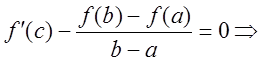
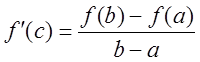 ; что и т. д.
; что и т. д.
Следствие: пусть ![]()
![]() ;
; ![]() .
. ![]() , где
, где
![]() .
.
Формула Лагранжа в
конечном приращении имеет вид: ![]() .
.
Теорема
Каши. Пусть функции ![]() и
и ![]() определены на некотором промежутке
определены на некотором промежутке ![]() и дифференцируемы внутри его, причем
и дифференцируемы внутри его, причем ![]() . Тогда существует хотя бы одна точка
. Тогда существует хотя бы одна точка ![]() в которой выполняются следующие условия.
в которой выполняются следующие условия.
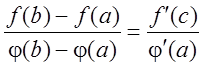 (1)
(1)
Доказательство: вводится
вспомогательная функция ![]() , удовлетворяющая всем
условиям теоремы Ролля:
, удовлетворяющая всем
условиям теоремы Ролля: 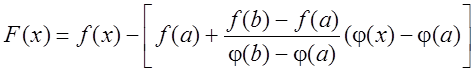
![]()
![]()
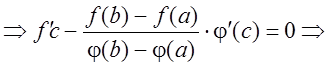
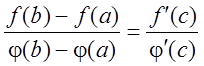 , что и требовалось
доказать.
, что и требовалось
доказать.
Пусть:
1. ![]() и
и ![]() -
дифференцируемы на
-
дифференцируемы на ![]() , и
, и ![]()
2. ![]()
3. существует
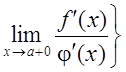 , тогда
, тогда 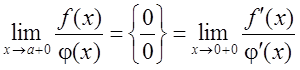
Т. е. при раскрытии неопределенности типа ![]() , если существует предел отношений
производных, то этот предел совпадает с пределом отношения самих функций.
, если существует предел отношений
производных, то этот предел совпадает с пределом отношения самих функций.
Доказательство: Пусть ![]() и
и ![]() . Тогда по теореме Каши
. Тогда по теореме Каши ![]() :
: 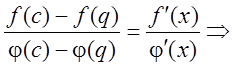
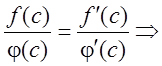
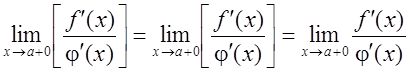 .
.
Правило Лапиталя применяют для раскрытия
неопределенностей типа ![]() ,
, 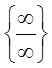 ,
, ![]() . Для
раскрытия неопределенностей типа
. Для
раскрытия неопределенностей типа ![]() ,
,![]() ,
,![]() ,
,![]() требуется предварительное
логарифмирование исходной функции.
требуется предварительное
логарифмирование исходной функции.
Примеры: 1.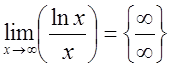 ; 2.
; 2.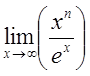 ; 3.
; 3.![]() 4.
4.![]() ; 5.
; 5.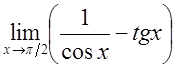 ; 6.
; 6.![]() ;
; ![]() ;
; ![]() ;
; ![]()
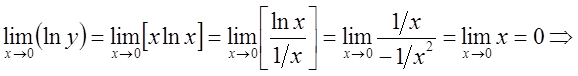
![]()
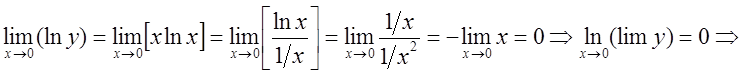
![]()
![]() .
.
Определение: функция ![]() определяется на интервале
определяется на интервале ![]() , называется возрастающей на этом
интервале, если большее значение аргумента соответствует большему значению
функции.
, называется возрастающей на этом
интервале, если большее значение аргумента соответствует большему значению
функции.
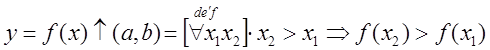 (1)
(1)
Аналогично,
функции ![]() будет убывающей на
будет убывающей на ![]() , если
, если
![]() (2)
(2)
Теорема: Необходимый признак монотонности функции
1. Если дифференциал на интервале ![]() функция
функция ![]() возрастает,
то на этом интервале ее производная
возрастает,
то на этом интервале ее производная ![]() неотрицательна, т. е.
неотрицательна, т. е.
![]() (3)
(3)
2. Если дифференциал на интервале ![]() функция
функция ![]() убывает,
то на этом интервале ее производная
убывает,
то на этом интервале ее производная ![]() неположительна, т. е.
неположительна, т. е.
![]() (4)
(4)
Доказательство: ![]()
![]()
![]()
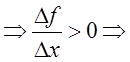
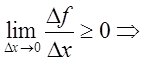
![]() , что и требовалось доказать. Аналогично
доказывается условие теоремы (4).
, что и требовалось доказать. Аналогично
доказывается условие теоремы (4).
Теорема: Достаточный признак монотонности функции
1. Если производная функции ![]() на
интервале
на
интервале ![]() существует и положительна, то на этом
интервале функция
существует и положительна, то на этом
интервале функция ![]() будет возрастающей, т. е.
будет возрастающей, т. е.
![]() (5)
(5)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.