Уравнение (5) называется каноническим уравнением эллипса.
Эллипс – центральная фигура с центром в точке О(0,0).
Точки пересечения эллипса с осями координат называются вершинами эллипса.
Ось, на которой расположены фокусы, называется фокальной осью.
Отрезок ![]() - называется большой
полуосью эллипса.
- называется большой
полуосью эллипса.
Отрезок ![]() - называется малой
полуосью эллипса.
- называется малой
полуосью эллипса.
Определение.
Отношение половины расстояния между фокусами эллипса к его большой полуоси
называется эксцентриситетом эллипса ![]() (6).
(6).
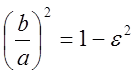 (7)
(7) ![]() - определяет форму эллипса.
- определяет форму эллипса.
Определение.
Если эллипс задан уравнением (5), где ![]() , то
прямые
, то
прямые ![]() - называются директрисами эллипса.
- называются директрисами эллипса.
Вычисление фокальных радиусов: ![]()
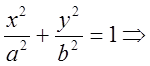
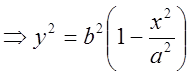 ;
; 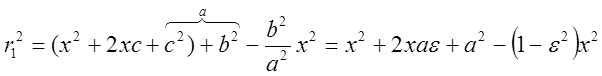
![]()
![]() (8).
(8).
Аналогично
выводится ![]() (9).
(9).
Теорема;
Отношение расстояния ![]() произвольной точки М эллипса до
фокуса F к расстоянию d от этой точки
до директрисы, ближайшей к этому фокусу, есть величина постоянная, равная
эксцентриситету эллипса, т.е.
произвольной точки М эллипса до
фокуса F к расстоянию d от этой точки
до директрисы, ближайшей к этому фокусу, есть величина постоянная, равная
эксцентриситету эллипса, т.е. 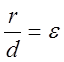 (10).
(10).
Доказательство.
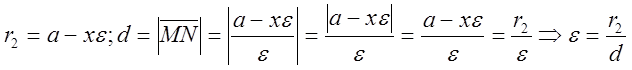 , что и т.д.
, что и т.д.
Определение. Гиперболой называют
геометрическое место точек, абсолютная величина разности расстояний каждой из
которых до двух фиксированных точек ![]() и
и ![]() , именуемых фокусами, есть величина
постоянная, равная
, именуемых фокусами, есть величина
постоянная, равная ![]() , причем
, причем ![]() .
.
Выбор системы координат: - такой же, как и у эллипса.
![]()
![]()
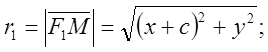
![]()
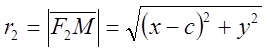 ;
; ![]()
![]()
![]() .
.
![]()
![]() (как
и для эллипса)
(как
и для эллипса)
![]()
![]() (11)
(11)
![]()
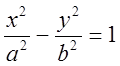 (12) – каноническое
уравнение гиперболы.
(12) – каноническое
уравнение гиперболы.
Эксцентриситет:
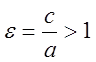 , где
, где ![]() -
большая (действительная) полуось;
-
большая (действительная) полуось; ![]() - малая (мнимая)
полуось.
- малая (мнимая)
полуось.
Директрисы:
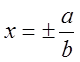 . Диагонали опорного прямоугольника
. Диагонали опорного прямоугольника 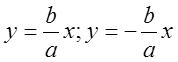 - служат асимптотами гиперболы. Все cвойства
директрис и эксцентриситета сохраняются и для гиперболы.
- служат асимптотами гиперболы. Все cвойства
директрис и эксцентриситета сохраняются и для гиперболы.
Определение.
Параболой называют геометрическое место точек, равноудаленных от некоторой
точки ![]() , именуемой фокусом, и некоторой прямой,
именуемой директрисой.
, именуемой фокусом, и некоторой прямой,
именуемой директрисой.
Выбор системы координат: ![]() -
параметр – расстояние от фокуса до директрисы;
-
параметр – расстояние от фокуса до директрисы; ![]() ; центр
О лежит посередине между фокусом и директрисой.
; центр
О лежит посередине между фокусом и директрисой.
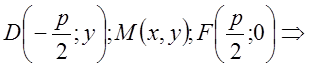
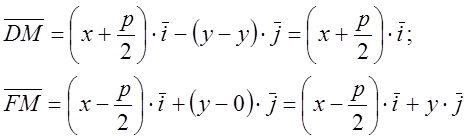
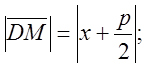
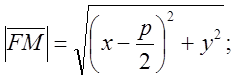
![]()
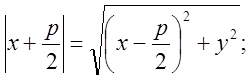
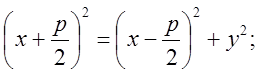
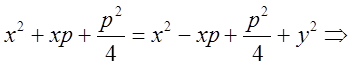
![]()
![]() - каноническое
уравнение параболы.
- каноническое
уравнение параболы.
1)
![]()
2)
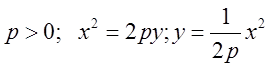 .
.
![]() - в старой системе координат;
- в старой системе координат;
![]() - в новой системе координат.
- в новой системе координат.
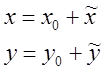
![]()
![]()
=![]()
![]()
![]()
Окончательно: 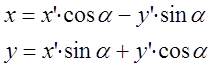 .
.
Различают центральные и нецентральные линии второго порядка.
Центр – точка на плоскости, по отношению к которой точки линии располагаются симметрично парами.
Кривая, обладающая единственным центром, называется центральной.
Осуществим параллельный перенос системы координат с целью уничтожения линейных элементов.
Имеем:
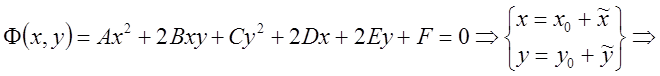
![]()
![]()
![]()
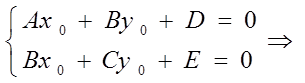
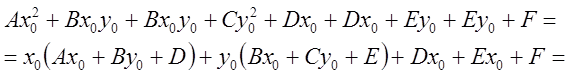
![]()
![]()
![]() , где
, где ![]() .
.
Для того, чтобы существовал
единственный центр ![]() , т.е. линия была центральной,
необходимо и достаточно, чтобы
, т.е. линия была центральной,
необходимо и достаточно, чтобы 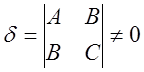 . Тогда координатами
центра будут:
. Тогда координатами
центра будут: 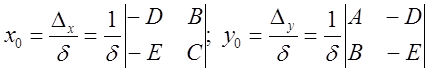 .
.
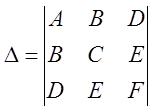 - дискриминант
левой части общего уравнения (1).
- дискриминант
левой части общего уравнения (1).
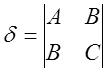 -
дискриминант старших членов уравнения (1).
-
дискриминант старших членов уравнения (1).
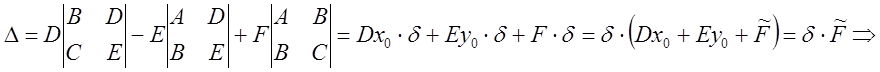
![]()
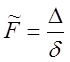 .
.
Вывод: 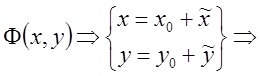
![]() , где
, где 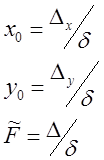 .
.
Для
получения канонического вида нужно убрать элемент ![]() , что
достигается поворотом осей вокруг нового центра
, что
достигается поворотом осей вокруг нового центра ![]() на угол
на угол
![]() .
.
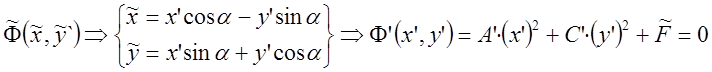 , где
угол поворота
, где
угол поворота ![]() выбирается из условия
выбирается из условия ![]() .
. ![]() связаны
между собой условиями:
связаны
между собой условиями: 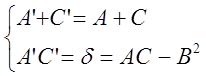 .
.
Определение: Уравнение второй степени называется эллиптическим,
если ![]() , гиперболическим, если
, гиперболическим, если ![]() , и параболическим, если
, и параболическим, если ![]() .
.
Примечание.
Упрощение параболического уравнения целесообразно начинать с поворота осей с
целью уничтожения элемента ![]() , а затем в новой
системе координат осуществить параллельный перенос вдоль той оси, которая
представлена высшей степенью в полученном результате.
, а затем в новой
системе координат осуществить параллельный перенос вдоль той оси, которая
представлена высшей степенью в полученном результате.
Пример.
Привести к простейшему (каноническому) виду уравнение кривой ![]() .
.
1)
![]()
2)
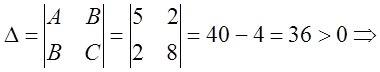 уравнение
эллиптического типа.
уравнение
эллиптического типа.
3)
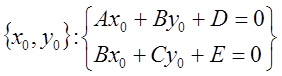 ;
;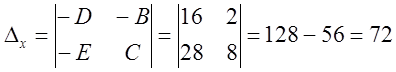 ;
;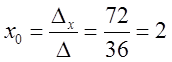
![]() - центр кривой.
- центр кривой. ![]()
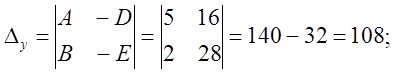
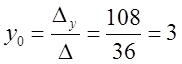 .
.
4)
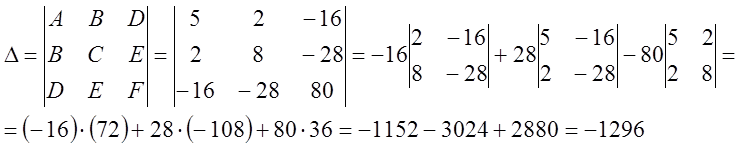
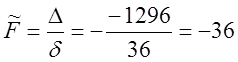 или
или ![]() .
.
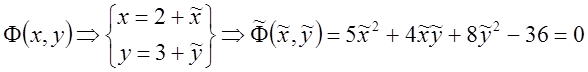
5)
![]()
![]()
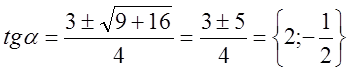 .
.
Выбираем ![]() (
(![]() - в
первой четверти)
- в
первой четверти)![]()
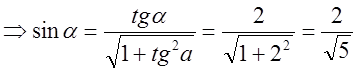 ;
; 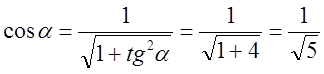 .
.
Имеем: 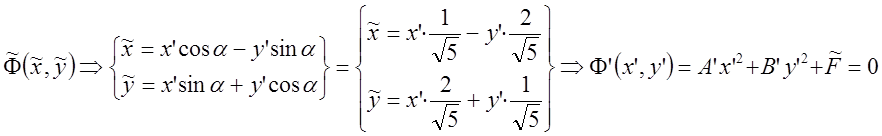 .
.
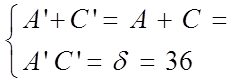
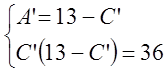
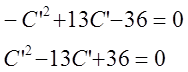
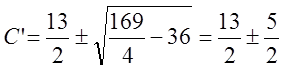
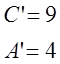
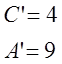
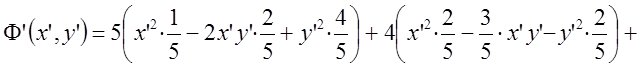
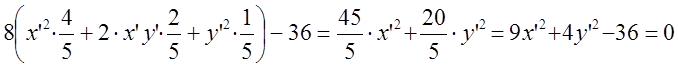
![]()
![]()
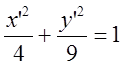
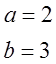
Пример №2. Упростить
уравнение линии: ![]() .
.
1)
![]()
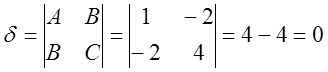 - параболический тип.
- параболический тип.
2)
![]()
![]()
![]()
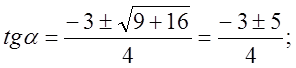
![]()
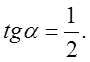 Пусть
Пусть 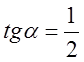
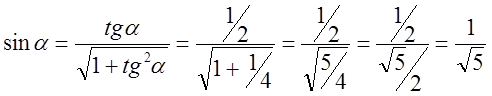 ;
; 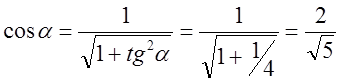 ;
;
Имеем: 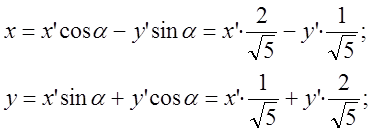
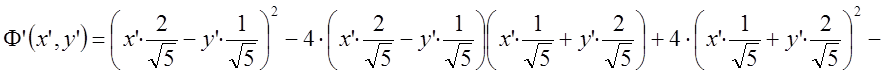
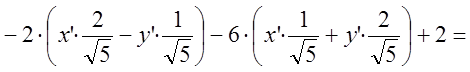
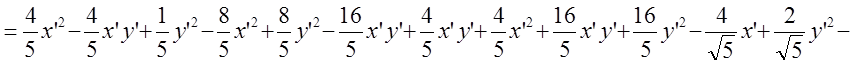
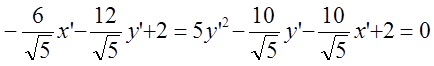
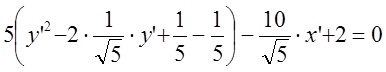
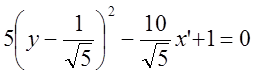
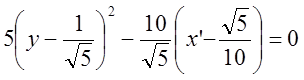
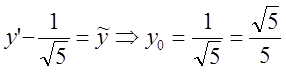
![]()
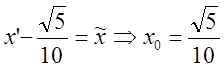
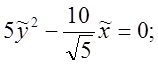
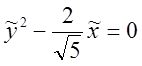 ;
; 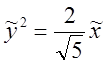
Определение: Вектор ![]() , перпендикулярный
плоскости
, перпендикулярный
плоскости ![]() , называется нормальным вектором этой
плоскости.
, называется нормальным вектором этой
плоскости.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.