![]() - выпукла на
- выпукла на ![]() (1)
(1)
Доказательство:
Пусть ![]() .
.
1. Выбираем
произвольную точку ![]()
2. Проводим
касательную к графику функции ![]() в точке касания
в точке касания ![]()
![]()
3. Находим
разность ординат ![]() в произвольной точке
в произвольной точке ![]() :
: ![]()
4. ![]() |по определению
Логранжа| =
|по определению
Логранжа| =![]() , где
, где ![]()
5. ![]()
6. ![]() |по определению Логранжа|
=
|по определению Логранжа|
= ![]() , где
, где ![]()
7.
------------------------------ разрыв страницы à конец страницы 54 -------------
------------------------------ разрыв страницы à начало страницы 00 -------------
Определение:
Если дано правило, согласно которому произвольному вектору ![]() плоскости a ставится в
соответствии вполне определенный вектор
плоскости a ставится в
соответствии вполне определенный вектор ![]() той же
плоскости, то говорят, что на плоскости задано преобразование векторов.
той же
плоскости, то говорят, что на плоскости задано преобразование векторов.
Вектор ![]() называется
называется ![]() =
=![]() *
*![]() образом вектора
образом вектора ![]() ,
а сам вектор
,
а сам вектор ![]() -прообразом вектора
-прообразом вектора ![]() .
.
Примечание. При работе со свободными векторами удобно предполагать, что они все исходят из одной точки О ( приложены к ней). Поэтому т. О при заданном преобразовании А всегда остается на месте.
Определение:
Преобразование ![]() =
=![]()
![]() называется линейным, если соблюдены
следующие два условия:
называется линейным, если соблюдены
следующие два условия:
1)
![]() , где
, где ![]() R,
R, ![]()
![]()
![]() ;
;
2)
![]() ,
, ![]()
![]()
![]() .
.
![]() =
=![]() ;
; ![]() =
=![]() *
*![]()
![]() ;
; ![]()
Так как ![]()
![]()
![]()
![]()
![]() =
=![]() то
то ![]() получается
из
получается
из ![]() таким же растяжением катит
таким же растяжением катит ![]() получается из
получается из ![]()
Второе условие означает, что каждый параллелограмм ![]() преобразуется в четырехугольник
преобразуется в четырехугольник ![]() который также является параллелограммом.
который также является параллелограммом.
Пример 1: Преобразование ![]() заключается в том, что все векторы растягиваются в
заключается в том, что все векторы растягиваются в ![]() раз:
раз: ![]() .
.
Так как 1) ![]()
![]()
![]()
![]()
![]() =
=![]()
![]()
![]()
![]()
![]() =
=![]() =
=![]()
2) ![]() =
=![]() =
=![]() =
=![]()
то данное преобразование является линейным. Такое
линейное преобразование называется подобием с коэффициентом подобия ![]() .
.
![]()
![]()
![]() =Х1Е1+Х2Е2
=> (Х1,Х2)-координаты
вектора
=Х1Е1+Х2Е2
=> (Х1,Х2)-координаты
вектора ![]() в
базисе
в
базисе ![]() . Пусть задано некоторое линейное
преобразование
. Пусть задано некоторое линейное
преобразование ![]() =
=![]()
![]() .
. ![]()
![]()
![]() , где
, где ![]() ;
; ![]() .
.
Теорема:
Для того, чтобы задать линейное преобразование А нужно задать образы ![]() базиса в виде их разложения по исходному
базису
базиса в виде их разложения по исходному
базису ![]() .
.
![]()
![]()
Доказательство: ![]() ;
; ![]()
![]() =
=![]() =А
=А![]() =А
=А![]() = =
= =![]() =
=![]() +
+![]() =
=![]() +
+![]() =>
=>
=> 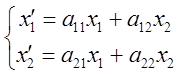 (3)
(3) 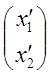 =А
=А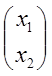 , где
А
, где
А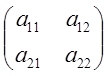 .
.
То есть для любого прообраза 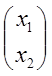 однозначно
определяется образ
однозначно
определяется образ 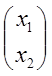 .
.
(3)-называетя координатным представлением данного
преобразования ![]() в базисе
в базисе ![]() . Матрица А=
. Матрица А=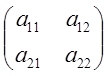 называется
матрицей линейного преобразования в данном базисе.
называется
матрицей линейного преобразования в данном базисе.
Теорема (обратная) : Пусть линейные преобразования формулами (3). Тогда образы базисных векторов однозначно определяется матрицей А этой системы.
Действительно ![]() =(1,0)
=(1,0)
![]() =(1,0)
=(1,0)
То есть вектор ![]() в
образе
в
образе ![]() имеет координаты (1,0). Аналогично
имеет координаты (1,0). Аналогично ![]() в образе
в образе ![]() имеет
координаты (0,1). Тогда по формуле (3):
имеет
координаты (0,1). Тогда по формуле (3):
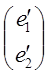 =А
=А![]() ;
; 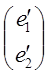 =
=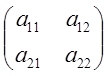
![]() =
=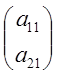 =>
=> 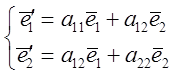 (4)
(4)
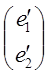 =Ат
=Ат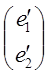 , где Ат транспортированная
матрица.
, где Ат транспортированная
матрица.
Вывод: Если дано линейное преобразование ![]() и выбран базис
и выбран базис ![]() ,
то данное преобразование представляется в координатах формулами (3). Обратно,
если марание даны формулы (3), то они представляют в выбранных координатах
некоторое линейное преобразование
,
то данное преобразование представляется в координатах формулами (3). Обратно,
если марание даны формулы (3), то они представляют в выбранных координатах
некоторое линейное преобразование ![]() . Матрица М1
составленная из коэффициентов системы (3) и матрица Ат, задающая
разложение (4) нового базиса
. Матрица М1
составленная из коэффициентов системы (3) и матрица Ат, задающая
разложение (4) нового базиса ![]() по старому базису
по старому базису![]() переводятся одна в другую
транспортированием.
переводятся одна в другую
транспортированием.
Пример: Пусть ![]() -есть
подобие с коэффициентом k, То есть
-есть
подобие с коэффициентом k, То есть ![]() .
.
Тогда ![]() =
=![]() =>
=> 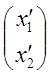 =k
=k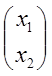 =>
=> ![]()
![]()
ð
А=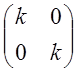 -матрица
подобия.
-матрица
подобия.
Пусть ![]() ;
; ![]() , То есть
, То есть ![]() ,
, ![]() . Тогда
. Тогда ![]() .
Преобразование (АВ) называется произведением А и В.
.
Преобразование (АВ) называется произведением А и В.
Теория: Матрица произведения (АВ) двух линейных преобразований равна произведению матриц этих преобразований.
Определение:
Линейное преобразование ![]() называется врожденным,
если определитель его матрицы А равен 0.
называется врожденным,
если определитель его матрицы А равен 0.
Пусть ![]() . Преобразование А-1
называется обратным по отношению к данному, если оно любому образцу
. Преобразование А-1
называется обратным по отношению к данному, если оно любому образцу ![]() ставит в соответствие его прообраз
ставит в соответствие его прообраз ![]() .
.
То есть ![]() .
.
Теорема: Для каждого невыраженного линейного преобразования имеется обратное, которое также является линейным и имеет матрицу А-1, обратную к матрице А.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.